Answers to exercises

Exercise 1

• Are 'diagonalise' and 'diagonalize' two words or the same word?
• Is the phrase 'deja vu' two English words? What about 'café'?
• Can we restrict English words to the words defined in the Oxford English Dictionary? Is the word 'gunna' defined? Was 'internet' in the Oxford English Dictionary in 1970?

Exercise 2

Let \(f(x) = \dfrac{x^2}{2} + x\).

1. \(f(3) = \dfrac{3^2}{2} + 3 = \dfrac{15}{2}\).
2. \(f(a+h) = \dfrac{(a+h)^2}{2} + a + h\).

Exercise 3

1. Let \(f(x) = \sqrt{(x-1)(x-2)}\). Then \(f(x)\) is defined if and only if \((x-1)(x-2) \geq 0\). So we sketch the graph of \(y=(x-1)(x-2)\).
   
   
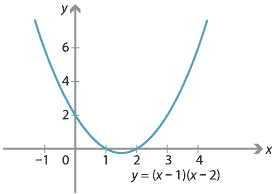
   Hence, \(\mathrm{domain}(f) = (-\infty,1] \cup [2,\infty)\) and \(\mathrm{range}(f)=[0,\infty)\).
2. Let \(g(x) = \sqrt{1-2\sin2x}\). To find the domain of \(g(x)\), we first note that \begin{align*} g(x) \text{ is defined} \ &\iff\ 1-2\sin2x \geq 0 \\ &\iff\ 2\sin2x \leq 1 \\ &\iff\ \sin2x \leq \tfrac{1}{2}. \end{align*} So we sketch the graph of \(y = \sin 2x\).
   
   
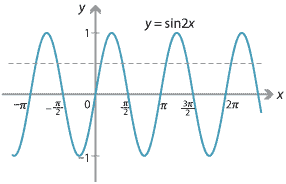
   Now solve \(\sin2x = \dfrac{1}{2}\) for \(x\): \begin{alignat*}{4} 2x &= \dfrac{\pi}{6} + 2k\pi &\quad&\text{or}\quad & 2x &= \dfrac{5\pi}{6} + 2k\pi, &\quad&\text{for some } k \in \mathbb{Z} \\ x &= \dfrac{\pi}{12} + k\pi &&\text{or} & x &= \dfrac{5\pi}{12} + k\pi, &&\text{for some } k \in \mathbb{Z}. \end{alignat*} It follows that \(\sin2x \leq \dfrac{1}{2}\) if and only if \(x\) belongs to the interval \(\Bigl[\dfrac{5\pi}{12}, \dfrac{13\pi}{12}\Bigr]\) or one of its translates by a multiple of \(\pi\). Hence, \[ \mathrm{domain}(g) = \bigcup_{k \in \mathbb{Z}}\, \Bigl[\dfrac{5\pi}{12} + k\pi, \dfrac{13\pi}{12}+k\pi\Bigr]. \] The maximum value of \(g(x)\) is \(\sqrt{1 - 2\times (-1)} = \sqrt{3}\). Hence, \(\mathrm{range}(g) = [0,\sqrt{3}]\).

Exercise 4

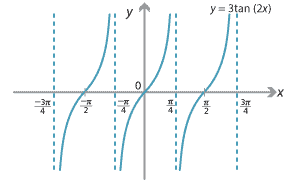
Let \(f(x)=3\tan 2x\). The domain of \(\tan x\) is all real numbers except odd multiples of \(\dfrac{\pi}{2}\), and the range of \(\tan x\) is all reals. Hence, \[ \mathrm{domain}(f) = \mathbb{R} \setminus \{\dots, -\tfrac{3\pi}{4}, -\tfrac{\pi}{4}, \tfrac{\pi}{4}, \tfrac{3\pi}{4}, \dots\} \] and \(\mathrm{range}(f) = \mathbb{R}\).

Detailed description

Exercise 5

1. 
   Detailed description
   
   \(\mathrm{domain}(f) = \mathbb{R}\) and \(\mathrm{range}(f) = \mathbb{Z}\).
2. 
   Detailed description
   
   \(\mathrm{domain}(g) = \mathbb{R}\) and \(\mathrm{range}(g) = [0,1)\).

Exercise 6

1. Arithmetic sequence with first term \(a=2\) and common difference \(d=3\).
2. Geometric sequence with first term \(a=3\) and common ratio \(r=-2\).
3. Geometric sequence with first term \(a=1\) and common ratio \(r=0.1\).
4. The Fibonacci sequence; it is neither geometric nor arithmetic.
5. This sequence is neither geometric nor arithmetic.

Exercise 7

\(\mathrm{domain}(f) = \mathrm{codomain}(f) = \mathbb{N}\) and \(\mathrm{range}(f) = \{3,5,7,9,11,\dots\}\).

Exercise 8

Assume \(A = \{a_1,a_2,\dots,a_m\}\) and \(B = \{b_1,b_2,\dots,b_n\}\). If we are defining a function from \(A\) to \(B\), then there are \(n\) choices for where to map \(a_1\), and then there are \(n\) choices for where to map \(a_2\), and so on. Thus the total number of functions is \(n^m\).