The Improving Mathematics Education in Schools (TIMES) Project
Year : 10
It is assumed that in Years 1-9, students have had many learning experiences that consider simple and everyday events involving chance, and descriptions of them. They have considered which events are, or may be assumed, more or less likely, and, if events are not more or less likely than others, then they have considered that it is reasonable to assume the events to be equally-likely. They have looked at simple everyday events where one cannot happen if the other happens, and, in contrast, they have thought about simple situations where it is reasonable to assume that the chance of occurrence of an event is not changed by the occurrence of another. They recognise impossible and certain events, and that probabilities range from 0 to 1. They have listed outcomes of chance situations for which equally-likely outcomes may be assumed. They have represented probabilities using fractions, decimals and percentages. They have had hands-on, real and virtual learning experiences in how probabilities can affect observations in both small and larger amounts of data (real and virtual), and have compared observed frequencies with expected frequencies corresponding to given or assumed sets of probabilities. In everyday simple situations, with a clear and easily listed number of possible outcomes that can, or may, be assumed to be equally-likely, they have considered probabilities of events by applying the concept of equal chances for equal “sizes” of events. They have generalised these to summing probabilities of disjoint events, including the special case of complementary events. Students have described, interpreted and represented events in more general situations, using the language of “not”, “at least” and “and”, and learned of the ambiguities in the use of the word “or”. In Year 9, students have considered situations involving two stages or two variables, including the special case of what are sometimes called two-step chance experiments. They have assigned probabilities based on assumptions, or estimated probabilities from data. Probabilities of events involving “and” or “or” have been determined from assumptions or estimated from data.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
Statistics is the science of variation and uncertainty. Concepts of probability underpin all of statistics, from handling and exploring data to the most complex and sophisticated models of processes that involve randomness. Statistical methods for analysing data are used to evaluate information in situations involving variation and uncertainty, and probability plays a key role in that process. All statistical models of real data and real situations are based on probability models. Probability models are at the heart of statistical inference, in which we use data to draw conclusions about a general situation or population of which the data can be considered randomly representative.
Probability is a measure, like length or area or weight or height, but a measure of the likeliness or chance of possibilities in some situation. Probability is a relative measure; it is a measure of chance relative to the other possibilities of the situation. Therefore, it is very important to be clear about the situation being considered. Comparisons of probabilities − which are equal, which are not, how much bigger or smaller − are therefore also of interest in modelling chance.
Where do the values of probabilities come from? How can we “find” values? We can model them by considerations of the situation, using information, making assumptions and using probability rules. We can estimate them from data. Almost always we use a combination of assumptions, modelling, data and probability rules.
The concepts and tools of probability pervade analysis of data. Even the most basic exploration and informal analysis involves at least some modelling of the data, and models for data are based on probability. Any interpretation of data involves considerations of variation and therefore at least some concepts of probability.
Situations involving uncertainty or randomness include probability in their models, and analysis of models often leads to data investigations to estimate parts of the model, to check the suitability of the model, to adjust or change the model, and to use the model for predictions.
Thus chance and data are inextricably linked and integrated throughout statistics. However, even though considerations of probability pervade all of statistics, understanding the results of some areas of data analysis requires only basic concepts of probability. The objectives of the chance and probability strand of the F-10 curriculum are to provide a practical framework for experiential learning in foundational concepts of probability for life, for exploring and interpreting data, and for underpinning later developments in statistical thinking and methods, including models for probability and data.
In this module, in the context of understanding chance and its effects in everyday life, we consider situations involving two or three stages or two or three variables, so that events may be described using “and” or with reference to other events. Some of the situations that involve two or three clear stages or steps are special cases that are sometimes called two- or three-step chance experiments, and some of these involve occurrences with or without replacement. Probabilities are assigned in these special cases to illustrate the effects of reference to previous occurrences. This re-visits the concept introduced in Year 4, namely, considering simple situations where it is reasonable to assume that the chance of occurrence of an event is not changed by the occurrence of another.
This leads to consideration of the language of “if”, “given”, “of”, “knowing that” and other similar or implicit language embedded in contexts. Everyday contexts with data in Year 9 examples are re-visited to consider events with reference to others, and statements involving the above language. Estimating probabilities from data in everyday situations help to illustrate this language. This also involves awareness of common mistakes in interpreting such language, and leads to investigation of the concept of independence without any formal definitions.
Concepts, assumptions, representations and the language of events and probability are experienced through examples of situations familiar and accessible to Year 10 students and that build on concepts and experiences introduced in Years 1-9.
Chance situations involving two or three steps
Simple chance situations involving two or three steps can illustrate the meaning of selection with or without replacement, and can illustrate probabilities of outcomes in the second or third step in relationship to earlier steps.
Example A: Throwing two or three dice or throwing one die twice or three times
If six-sided dice are each fair and are well shaken in a container before throwing, there is no difference statistically between throwing two or three dice and throwing one die twice or three times. The outcomes can be expressed by using “and”. For example, we can denote the first die by A and the second by B, and the third by C, with A1 meaning the first die gives a “1”. Hence “A1 and B1 and C2” is the event that the first die gives a 1, the second die gives a 1 and the third die gives a 2.
Does the outcome of the first die affect the outcome of the second? Of the third? When is it reasonable to assume that they don’t. Certainly the values that are possible are not affected. We can still get any of the values 1 to 6 on any subsequent toss of the die. In previous considerations of this situation, we have considered that if the dice are fair and if they are well-shaken before tossing, there is no reason to assume other than equally-likely faces, and no reason to assume other than equally-likely pairs of values in two throws and hence triples of values in three throws. Looking at this slightly differently, if we throw one die first, and then throw the second and third dice, provided the dice are fair and shaken well before throwing, there is no reason to assume that the second throw of the die is in any way affected by the outcome of the first throw. We would expect the probabilities of the 6 faces on the second throw to be 
no matter what happened on the first throw.
Example B: What colour sweets did you get?
Suppose you have a small box of different coloured sweets, such as M&M’s or Smarties. You give two or three to your friend by shaking one out of the box onto your friend’s hand and then by shaking out a second and possibly a third sweet onto your friend’s hand. If the colours of sweets in the box are red, yellow, green, blue, then, as in Example A, we can denote the results using “and”. For example 1R could be used to denote that the first sweet is red, so the event “1R and 2Y” is getting a red sweet first, then a yellow sweet second. The event “1R and 2Y and 3B” is the event getting a red sweet first, then a yellow sweet second, then a blue sweet third.
If we get a red sweet first, how will this affect the chance of getting a yellow sweet second? The red sweet is not replaced, so with a red sweet removed, the chances of getting a yellow sweet are increased on the second shake of the box. For the third shake, with both a red and a yellow sweet removed, the chance of getting a blue sweet is increased.
Putting some numbers to this, suppose we have equal numbers of the four colours in the box, say 10 each. Then the chance of getting a red sweet first is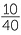 
= 0.25. Once a red sweet is removed, on the second shake of the box, we have 39 sweets with 10 yellow. So the chance of getting a yellow sweet second after getting a red sweet first is 
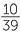. With both a red and a yellow sweet removed, the chance of then getting another yellow on the third shake is 9/38. This is certainly different to the chance of getting a yellow on the first shake, and it is because the sweets are being removed from the box.
Example C: Prizes in raffles
Raffles are usually run by people buying numbered (and sometimes coloured) tickets with the tickets being in two parts. The buyers keep one part and the other parts (we’ll call them the ticket stubs) are put into a container with someone picking out a ticket at random from the container. The outcomes of the draw are all the tickets that have been sold.
Usually there is more than 1 prize in a raffle, and often more than two. Let’s consider that the first draw is for third prize, the second draw for the second prize and the third draw is for the major prize. The tickets that are drawn are not put back, so this is another example of selection without replacement.
If 1000 tickets are sold, and you buy 2 tickets, the chance of your winning the third prize is 
. If you win the third prize (with one of your tickets), the chance of your then also winning the second prize is 
and the chance of not winning the second prize is 
. As in Example B, the chance of winning second prize is affected by whether you win third prize or not.
Can we easily find the chance of your winning at least one of the prizes? It is often easier to find the chance of at least one event happening by considering its complement and subtracting that probability from 1. What is the opposite of winning at least one of the prizes? It is winning none. The outcomes of the three draws are triples of distinct numbers and there are 1000 × 999 × 998 different selections that can be made. If the draws are random, then these can all be considered equally-likely. The number of these that don’t contain either of your tickets is 998 × 997 × 996. So the chance that you win nothing is (998 × 997 × 996)/(1000 × 999 × 998) = 0.994. So the chance you win at least one prize is 1 − 0.994 = 0.006.
The language and applications of conditional statements
in everyday situations involving estimation of probabilities
The simple situations of Examples A to C above are situations where considering whether the chance of an event is affected by the occurrence of another event is straightforward because
- there is a definite sequence of events − first, second, third etc;
- assumptions of equally-likely probabilities and hence probabilities proportional to “size” of events are straightforward to justify;
- assumption that the chance of an event happening is not affected by the occurrence of others is straightforward to justify;
- where the chance of an event happening is affected by the occurrence of another, it is due to selection without replacement.
Hence there tend to be few problems in the simple situations of Examples A to C with the language and applications of conditional statements.
We now consider simple everyday situations involving two or three stages or two or three variables (that take values in categories). In such situations, we are often interested in describing events in relation, or with reference to, other events. This is when the language of “if”, “of”, “given”, “knowing that”, “for” etc, tends to arise. The examples below are examples in Year 9 re-visited to consider events and questions that arise naturally from the discussions in Year 9. Using data to estimate probabilities of events with reference to other events, is of great assistance in understanding this language, and also in identifying common mistakes in interpreting such language.
Example D: Does the baby have dark or light eyes?
It seems that people always ask about the eye colour of a baby and whether the baby has eye colour similar to the mother or father. There are many different ways we could describe eye colour but the two main classifications are light and dark. So to talk about, say, the father’s eye colour and the baby’s eye colour, we can denote father’s eye colour light by FL, and baby’s eye colour light by BL, so that the event “FL and BL” is the event father’s eye colour is light and baby’s eye colour is light.
We may be interested in whether the baby’s eye colour is light, knowing the father’s eye colour. This may be expressed in any of the following ways:
- if the father’s eye colour is light, what is the chance the baby’s eye colour is light too
- knowing that the father has light eye colour, what is the chance the baby will have light eye colour?
- for fathers with light eye colour, what is the chance their baby will have light eye colour?
- given that the father’s eye colour is light, what is the chance that the baby’s eye colour is light?
- what proportion of fathers with light eye colour have a baby with light eye colour?
All of the above are asking the same question.
This also could be a three-stage situation that considers both parents. Note that these questions are different to the pure genetic questions that consider combinations of genes.
Consider the data in the table below.
| Child’s Eye Colour | Father’s Eye Colour | ||
| Light | Dark | ||
| Light | 471 | 148 | 619 |
| Dark | 151 | 230 | 381 |
| 622 | 378 | 1000 | |
If we consider only the data relating to fathers with light eye colour, we are considering only 622 of the 1000 observations. Of these 622 fathers, 471 have their child having light eye colour. Hence we can estimate the above chance, no matter how it is expressed, by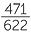 
= 0.757.
Similarly, we can estimate the chance of a dark-eyed father having a baby with light colour eyes by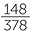 
= 0.392.
Notice that the above sentence provides yet another variation in the language − all of which are expressing the same event.
Even allowing for data variation, these are quite different − as we would expect!
Example E: Clasping hands and folding arms
When you clasp your hands, which thumb is on top? When you fold your arms, which arm is on top? Almost everyone finds that when they clasp their hands, the same thumb tends to be on top and it is very difficult to clasp such that the other thumb is on top. This observation, plus scientific articles such as the one at http://humangenetics.suite101.com/article.cfm/dominant_human_genetic_traits, do tend to indicate that it is a characteristic an individual is born with − a genetic trait. The article includes the following statement:
“Clasp your hands together (without thinking about it!). Most people place their left thumb on top of their right and this happens to be the dominant phenotype. Now, for fun, try clasping your hands so that the opposite thumb is on top. Feels strange and unnatural, doesn’t it?”
Folding arms has not received the same type of attention, possibly because it is easier to fold your arms differently to your usual way. But, similarly to clasping hands, people do tend to fold their arms the same way each time. For arm folding, we can just describe the outcome by which (fore) arm is on top, or we can distinguish further by whether one hand, no hands or both hands are showing. As in previous examples, we can denote these using “and”. For example, if we use the letter T to denote thumb and A to denote arm, then we can denote the outcome left thumb on top in clasping hands by TL, and left arm on top in folding arms with 1 hand showing, by the event “TL and AL1”.
Considering “and” statements is one way of looking at the connection between these two actions (clasping hands and folding arms) which may have a genetic link or possibly a genetic predisposition. However, in considering such links, we usually tend to express them in conditional statements such as the following:
- what is the chance that someone who has their left thumb on top in clasped hands, also puts their left arm on top when they fold their arms?
- if someone puts their left thumb on top when they clasp their hands, what is the chance they put their left arm on top when they fold their arms?
- what is the chance someone puts their left arm on top when they fold their arms if they put their left thumb on top when they clasp their hands?
- what proportion of people who put their left thumb on top when clasping hands, also put their left arm on top when folding arms.
All the above are asking the same question expressed slightly differently. In the question, the event TL is given − we are considering the event AL knowing the event TL has occurred.
Consider the data below.
| Upper arm and number of hands showing in folding arms | |||||||
| Upper thumb in clasping hands | AL0 | AL1 | AL2 | AR0 | AR1 | AR2 | Total |
| TL | 17 | 51 | 9 | 12 | 50 | 4 | 143 |
| TR | 16 | 37 | 8 | 13 | 36 | 6 | 116 |
| Total | 33 | 88 | 17 | 25 | 86 | 10 | 259 |
If we restrict attention to the event TL, we are considering only 143 of the observations.
Of those observations, 17 + 51 + 9 have their left arm on top, so the estimate of the chance described in all the above statements is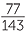 
= 0.54.
What is the relative frequency 
estimating? It is estimating the chance that a person who places their left arm on top in folding arms, also places their left thumb on top in clasping hands. Notice that both of these are not only different to each other but are also different to the chance that a person places their left arm on top in folding arms and also places their left thumb on top in clasping hands.
What about the people who place their right thumb on top? Based on the above data, an estimate of the chance that a person places their left arm on top in folding arms if they place their right thumb on top in clasping hands, is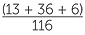 
= 
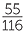= 0.474. Although this is less than 0.54, we must remember that these are estimates from data and hence we must allow for data variation. At this stage we do not have sufficient formal tools to understand how much variation to allow for, but the estimates are not greatly far apart. The overall proportion of people in this dataset who place their left arm on top in folding arms is 
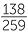= 0.533, so these data seem to indicate that whether people place their left thumb on top in clasping hands or their right, the chance of placing their left arm on top in folding arms is not much different to each other and not much different to 0.5.
The above questions consider only the position of the arm, but the above data can consider further refinements such as the chance of someone having both hands showing in folded arms if their left thumb is on top in clasping hands and their left arm is on top in folding arms. Using the above data, this can be estimated by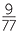 
.
Example F: Do people tend to underestimate or overestimate time?
How well do people estimate periods of time such as 5 seconds and 10 seconds. Is there a tendency to overestimate or underestimate? For an experiment in which people estimate 5 secs first and then 10 seconds, we could record the actual times they guessed, or simply record whether they underestimated or overestimated. If we decide that being out by less than 0.5 second is close enough to be regarded as correct, we could denote events using “and”. For example, “U5 and U10” is the event that a person underestimates 5 seconds and underestimates 10 seconds.
|
10 second guess |
||||
| 5 second guess | C10 | O10 | U10 | Total |
| C5 | 21 | 9 | 19 | 49 |
| O5 | 4 | 6 | 4 | 14 |
| U5 | 9 | 5 | 43 | 57 |
| Total | 34 | 20 | 66 | 120 |
Based on these data, we can estimate the probability that a person who underestimates
5 seconds also underestimates 10 seconds, by 
= 0.75.
Knowing that a person underestimates 10 seconds, what is the chance he or she will underestimate 5 seconds? This can be estimated by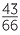 
.
No matter how a question is expressed, we can always identify what is given, known or the “reference” event.
Based on these data, we can estimate the probability that a person who correctly estimates 5 seconds underestimates 10 seconds, by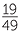 
= 0.39, and the probability that a person who overestimates 5 seconds then underestimates 10 seconds, by 
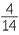= 0.29. Hence, even allowing for data variation, these data seem to indicate that a person’s estimation of 10 seconds is influenced by how they estimated 5 seconds.
Example G: Do people tend to take coloured
or white flyers?
Flyers advertising events or publicising views are often offered to passersby on busy pedestrian ways. What makes people accept or refuse a flyer? Would coloured ones be more likely to be accepted? If a person handing out flyers had a mixture of white and coloured ones, we have a two-stage or two-variable situation with outcomes consisting of colour of flyer and whether the passerby offered the flyer accepts of does not accept it. If this experiment (or observation) is also carried out in the morning and afternoon, and these are also recorded, we have data on three variables.
The data below give the frequencies for accepting (A) or rejecting (R) flyers offered to passersby in a busy pedestrian area in a city. The flyers had either a white background (W) or blue (B) but were otherwise identical. The flyers were simply offered to people to take or not with no attempts to engage the passersby in any way. The data were collected in both morning and afternoon, and the overall table is split into two tables below to consider morning and afternoon separately.
| Overall | Reaction | ||
| Colour | A | R | Total |
| B | 220 | 186 | 406 |
| W | 220 | 252 | 472 |
| Total | 440 | 438 | 878 |
| Morning | Reaction | Afternoon | Reaction | |||||
| Colour | A | R | Total | Colour | A | R | Total | |
| B | 110 | 68 | 178 | B | 110 | 118 | 228 | |
| W | 110 | 76 | 186 | W | 110 | 176 | 286 | |
| Total | 220 | 144 | 364 | Total | 220 | 294 | 514 | |
Notice that the numbers of white and blue flyers that are accepted are equal. Even if they aren’t equal, we would have a fixed quantity of each and would mix them up before handing them out, and clearly flyers will be handed out until they’re all gone. Although we could look at events using “and”, such as “a person is offered a blue flyer and accepts”, the situation clearly is more appropriately considered through “if” statements. For example, if a person is offered a blue flyer, what is the probability they will accept it? If a person is offered a blue flyer in the morning, what is the probability they will accept it?
Based on these data, we can estimate the probability that:
- overall a person accepts a blue flyer, by
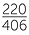= 0.54; - overall a person accepts a white flyer, by
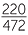= 0.47; - in the morning a person accepts a blue flyer, by
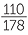= 0.62; - in the morning a person accepts a white flyer, by
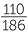= 0.59; - in the afternoon a person accepts a blue flyer, by
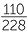= 0.48; - in the afternoon a person accepts a white flyer, by
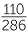= 0.385.
So in the morning there’s very little difference between the chances of accepting a blue or a white flyer. In the afternoon, there seems to be more difference, but the most interesting aspect is the contrast between morning and afternoon!
Note that the chance in the morning that a person accepts a blue flyer is the chance that a person accepts a flyer given that it’s blue and it’s offered in the morning. This can also be expressed as the chance of accepting a blue flyer if it’s offered in the morning.
In all the above examples, we see that the choice of expression of the statements is influenced by convenience and language preferences, and depends to at least some extent on the contexts. In any conditional statement, events for one variable or stage are considered with reference to events for at least one other variable or stage. To identify what is given, questions such as the following are of assistance:
- to what group or situation are we referring to? For example, is it in the morning?
Are we just considering males? - is there a qualifier or an adjective that tells us to what group we are referring?
For example, “a person who underestimates 5 seconds” tells us that “underestimating
5 seconds” is the given event − we are restricting attention to those who underestimate 5 seconds. If a person is offered a blue flyer, we are considering what happens given a blue flyer is offered; - is there a phrase starting with “if”, “for”, or “of”? Each of these can indicate a given condition. For example “if a person underestimates 5 seconds…”.
Mistakes are made when either the condition is not made clear or is misread, or when it is not understood how to estimate the probability from data. The above examples are selected to assist with both these aspects. A very simple example illustrating “if” statements, such as “A Granny Smith apple is green” compared the incorrect “If an apple is green, then it is a Granny Smith”, can help students understand the difference for situations involving chance. Simple statements involving chance that can help students understand the difference are statements such as “the chance that a boy plays soccer” compared with “the chance that a soccer player is a boy”.
For using data such as in the above examples to estimate chances of conditional statements, first identify the conditions, possibly by re-writing the conditional statement in a longer or different form that clearly identifies what is “given”. We see from the above examples, that the denominator in the relative frequency is then the number of observations that meet what is “given”. The numerator is the number that meet what is “given” AND meet the event for which the probability is wanted.
In an official survey such as the ABS survey on Children’s Participation in Cultural and Leisure Activities Survey (report 49010.0 on https://www.abs.gov.au/ausstats/abs@.nsf/mf/4901.0), frequencies are often reported separated into age groups or regions. Relative frequencies within age groups or regions (or both) are therefore estimates of population proportions conditional on the age group or region (or both).
In the discussion in each of the examples D to G above, the concept of independence is a natural one to consider. If the chance of an event is affected by the occurrence of another event, then these events are not independent. So if the chance that a person underestimates 10 seconds if they underestimate 5 seconds is not the same as the chance of underestimating 10 seconds if they overestimate 5 seconds, then underestimating 10 seconds depends on whether they under- or over-estimated 5 seconds.
If the chance of placing the left arm on top in folding arms is the same for those who place their left thumb on top in clasping hands as for those who place their right thumb on top, then position of arm on folding arms and position of thumb on clasping hands are independent.
In estimating from data, we must allow for data variation. So in Example G, there’s not much indication of a difference between the effects of white and blue flyers on the chance of acceptance in the morning, but possibly a bit more of an indication in the afternoon. However the contrast is between the morning and the afternoon. The data indicate that accepting a flyer, whether white or blue, appears to depend on whether the flyer is offered in the morning or the afternoon.
From Years 1-9, students have gradually developed understanding and familiarity with simple and familiar events involving chance, including possible outcomes and whether they are “likely”, “unlikely” with some being “certain” or “impossible”. They have seen variation in results of simple chance experiments. They have considered how to describe possible outcomes of simple situations involving games of chance or familiar everyday outcomes, and simple everyday events that cannot happen together or, in comparison, some that can. Consideration of the possible outcomes and of the circumstances of simple situations has lead to careful description of the events and assumptions that permit assigning probabilities.
Students have assigned and used probabilities in terms of fractions, decimals and percentages and considered the implications of probabilities for observing data in situations involving chance. They have collected data and carried out simple simulations of data to observe the effects of chance in small and larger sets of data.
In special, limited situations with a clear and easily listed number of possible outcomes that can, or may, be assumed to be equally-likely, students have considered probabilities of events by applying the concept of equal chances for equal “sizes” of events, and have collected data to compare observed frequencies with expected frequencies under the assumption of equally-likely probabilities. Students have seen that these are a special case of finding probabilities of events by summing probabilities of the disjoint (or mutually exclusive) outcomes making up the event, including the special case of complementary events. Students have explored, understood and used the language of “not”, “and”, “at least” and “or” as connectors in describing events in terms of others.
Students have considered situations involving two stages or two variables, including the special case of what are sometimes called two-step chance experiments. They have assigned probabilities based on assumptions, or estimated probabilities from data. Probabilities of events involving “and” or “or” have been obtained or estimated from data.
In Year 10, students have considered situations involving two or three stages or two or three variables. In the special case of two or three step chance experiments, they have assigned probabilities to outcomes in situations involving selections either with or without replacement. In simple everyday situations, they have explored and used the language of “if”, “given”, “of”, “knowing that”. By using data in everyday situations to estimate probabilities of statements involving this language, they have had a range of learning experiences with this language as well as in using relative frequencies to estimate probabilities of the associated conditional statements. This also helps to develop awareness of common mistakes in interpreting such language, and has led to the introduction of the concept of independence without any formal definitions.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
