The Improving Mathematics Education in Schools (TIMES) Project
Data Investigation and interpretation 9
Statistics and Probability : Module 7![]() Year : 9
Year : 9
June 2011
It is assumed that in Years F-8, students have had many learning experiences involving choosing and identifying questions or issues from everyday life and familiar situations, planning statistical investigations and collecting or accessing data, and have become familiar with the concepts of statistical variables and of subjects of a data investigation. It is assumed that students are now familiar with categorical, count and continuous data, have had learning experiences in recording, classifying and exploring individual datasets of each type, using tables and column graphs for categorical data and count data with a small number of different counts treated as categories, and dotplots and stem-and-leaf plots for continuous and count data. It is assumed that students are familiar with the use of frequencies and relative frequencies of categories (for categorical data) or of counts (for count data) or of intervals of values (for continuous data), and that students have used and interpreted averages (that is, sample means), medians and ranges of quantitative (that is, count or continuous) data. Students have used tables and graphs to explore more than one set of categorical data on the same subjects. In doing so, they have understood that they were investigating data on pairs of categorical variables.
Through learning experiences in many familiar and everyday contexts, students have come to recognise the need for data to be obtained randomly in circumstances that are representative of a more general situation or larger population with respect to the issues of interest. Students have examined the challenges of obtaining randomly representative data, emphasizing the importance of clear reporting of how, when and where data are obtained or collected, and of identifying the issues or questions for which data are desired to be representative. In years up to Year 8, students have seen a variety of examples of collecting data, and Year 8 has identified the difference between taking a census and collecting a sample of data, with explicit focus on surveys and observational studies.
In order to understand how to interpret and report information from data, students have developed some understanding of the effects of sampling variability. Focus on such effects has been implicit throughout data investigations in years up to Year 8, and explicit in Year 8 through the use of real data and simulations, including re-sampling from real data to illustrate how sample data and data summaries such as sample proportions and averages can vary across samples.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
A natural environment for learning statistical thinking is through experiencing the process of carrying out real statistical data investigations from first thoughts, through planning, collecting and exploring data, to reporting on its features. Statistical data investigations also provide ideal conditions for active learning, hands-on experience and problem-solving. No matter how it is described, the elements of the statistical data investigation process are accessible across all educational levels.
Real statistical data investigations involve a number of components: formulating a problem so that it can be tackled statistically; planning, collecting, organising and validating data; exploring and analysing data; and interpreting and presenting information from data in context. No matter how the statistical data investigative process is described, its elements provide a practical framework for demonstrating and learning statistical thinking, as well as experiential learning in which statistical concepts, techniques and tools can be gradually introduced, developed, applied and extended as students move through schooling.
In this module, in the context of statistical data investigations, we build on the content of Years F-8 to focus more closely on commenting on features of quantitative (continuous or count) data, and comparing quantitative data across the categories of one or more categorical variables. Histograms are introduced and used in these comparisons along with stem-and-leaf plots, always emphasizing the need for the same scale in plots when the aim is comparisons of data features. Comparisons are made using the summary statistics of sample means, medians and ranges, together with consideration of plots in commenting on location and spread. The concepts of symmetry, asymmetry and skewness are introduced to extend comments on data features to include introductory ideas of shape. In considering the effects of bin choice in histograms, together with awareness of the need to allow for sampling variability, we see that great caution is needed in any use of the term “bimodal” in describing data. Generally, the use of this term should be avoided unless a variety of plots of the data together with consideration of the context indicate that there may be a mixture of groups in the data. In such cases, we can often use a categorical variable to separate such groups.
Throughout this module, students build on their understanding that to use data to comment on questions and issues, we need the data to be a random set of observations obtained in circumstances that are representative of the general situation or population with respect to the questions or issues of interest. All the examples considered in this module are of datasets collected by students to investigate questions or issues chosen by the students themselves. The investigations involve designing experiments, observational studies or surveys or a mixture of these types of investigations. The importance of randomisation in designing experiments is emphasized, as is the importance of clear reporting of how, when and where data are obtained or collected, and of identifying the issues or questions for which data are desired to be representative. The module concludes with a summary of the nature of censuses, surveys, observational and experimental investigations.
The examples and new content of this module are developed within the statistical data investigation process through the following:
- considering initial questions that motivate an investigation;
- identifying issues and planning;
- collecting, handling and checking data;
- exploring and interpreting data in context.
Such phases lend themselves to representation on a diagram, as follows.
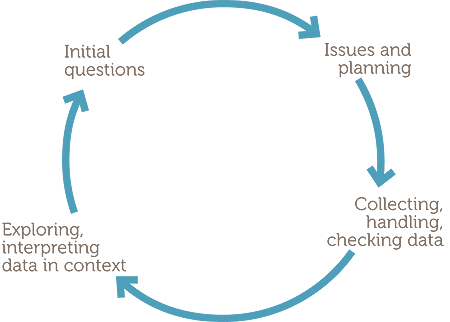
The examples consider situations familiar and accessible to Year 9 students and build on situations considered in F-8. The module uses concepts, graphs and other data summaries considered in F-8, and introduces further concepts and graphs to focus on features of quantitative data, particularly data on continuous variables, and comparisons of features of such data across categories of one or more categorical variables.
Revision of types of data and
statistical variables
In F-8, we have considered different types of data, and hence different types of statistical variables. When we collect or observe data, the ‘what’ we are going to observe is called a statistical variable. You can think of a statistical variable as a description of an entity that is being observed or is going to be observed. Hence when we consider types of data, we are also considering types of variables. There are three main types of statistical variables: continuous, count and categorical.
Some examples of continuous variables are:
- time in minutes to get to school
- length in cm of right feet of Year 7 girls
- age in years
- amount of weekly allowance
All continuous data need units, and observations are recorded in the desired units.
Continuous variables can take any values in intervals. For example, if someone says their height is 149 cm, they mean their height lies between 148.5 cm and 149.5 cm. If they say their height is 148.5 cm, they mean their height is in between 148.45 cm and 148.55 cm. If someone reports their age as 14 years, they (usually) mean their age is in between 14 and 15 years. Note the convention with age is that the interval is from our age in whole number of years up to the next whole number of years. Our specification of intervals in talking about age is usually not as definite as when we quote someone’s height, but the principle is the same − observations of continuous variables are never exact and correspond to intervals, no matter what the size of the interval.
A count variable counts the number of items or people in a specified time or place or occasion or group. Each observation in a set of count data is a count value. Count data occur in considering situations such as:
- the number of children in a family
- the number of people arriving at a central city railway station in a 5 minute interval during peak time
- attendance at football matches
- the number of hits on an internet site per week
We can see that the first example above of a count variable contrasts with the other examples, in which counts will tend to take many different values − that is, in data on the variables in bullet points 2, 3 and 4 above, repetitions of values of observations are not likely. Also, the sizes of the observations will tend to be large, sometimes very large. For these types of count variables, the types of graphs and summaries used for continuous variables are often appropriate.
In categorical data each observation falls into one of a number of distinct categories. Thus a categorical variable has a number of distinct categories. Such data are everywhere in everyday life. Some examples of pairs of categorical variables are:
- gender and pet preference between cat and dog
- favourite TV show and favourite holiday activity
- gender and favourite food
- favourite sport and colour of hair (e.g. redhead, blonde, brown, black)
Sometimes the categories are natural, such as with gender or preference between cat and dog, and sometimes they require choice and careful description, such as favourite holiday activity or favourite food.
Data investigations initiated, planned
and carried out by students
The following are some examples of data investigations initiated, designed and undertaken entirely by students, and involving a number of variables including at least one quantitative variable and at least one categorical variable. The groups of students involved chose their context and the aspects of it of interest to them, identified the variables and subjects of the investigation, planned the practicalities of the data collection to obtain randomly representative data, carried out appropriate pilot studies and collected their data, then explored and reported on their data.
In the first part of the data investigative process, one or more questions or issues begin the process of identifying the topic to be investigated. In thinking about how to investigate these, other questions and ideas can tend to arise. Refining and sorting these questions and ideas along with considering how we are going to obtain data that is needed to investigate them, help our planning to take shape. A data investigation is planned through the interaction of the questions:
- ‘What do we want to find out about?’
- ‘What data can we get?’ and
- ‘How do we get the data?’
Planning a data investigation involves identifying its variables, its subjects (that is, on what or who are our observations going to be collected) and how to collect or access relevant and randomly representative data.
For each example below, the students were interested in a number of questions and issues, only some of which are explored in this module.
Example A: How often do people blink?
How often do people blink? How variable are people? Are males and females different in how often they blink? These were the questions that motivated a group of students to investigate frequency of blinking. However to record how often people blink requires close observation which is highly likely to be noticed by subjects and interfere in either the data collection or in the subject’s blinking or both. Hence the students decided that they needed to create conditions that would enable them to collect data under similar controlled circumstances.
They decided to conduct a simple survey on opinions on a topic such as travel, asking questions for one minute. There were four students in the group and they collected their data in pairs. One member of the pair asked the questions while the other unobtrusively counted the number of times each subject blinked. They approached their subjects asking if they minded answering a short survey on travel. As soon as the minute was completed, they stopped asking questions and explained they had been counting the number of blinks and asked if the person was happy to have their recorded number of blinks included in a dataset in which anonymity would be preserved and which would be used only for a student project.
The students used the same questions, and stayed in the same pairs of investigators to collect their data. They approached fellow students as randomly as possible, and, as this study involves physical attributes, their data can be reasonably assumed to be randomly representative of students in the age group they approached. The student investigators recorded the gender and age of the subject, the number of blinks in the minute of the survey, whether the questions were asked inside or outside, in the morning or afternoon, the subject’s eye colour, and whether the subject wore glasses or not. They also recorded the pair who collected the data for each subject. They discovered during their exploration of the data that this last variable was important. It happened by accident more than design, that the group of two boys and two girls decided to collect their data in same gender pairs − that is, the two girls formed one pair of collectors and the two boys formed the other pair. In this module, we consider the number of blinks per minute, the gender of the subject and the gender of the observer pair, but in practice, as with other examples in these modules, all of the variables are likely to be of interest, and it is likely that combinations of variables could affect the number of blinks.
Example B: optical illusions
There are pictures that can be looked at in two ways. For example, there is a well-known father and son optical illusion (see, for example, http://www.moillusions.com/2010/07/father-and-son-optical-illusion.html ). This example is considered in the Year 6 module from the point of view of which picture do people tend to see first, and to compare this for boys and girls, and the Year 7 module looks at how long people tend to take to see a picture − no matter which one they see first. The group of students who thought of this topic were interested not only in which picture people saw first and how long they took in seeing it, but also whether they were interested in seeing the other picture and whether they were right or left-handed. The investigators also recorded each subject’s gender and age.
The student investigators also originally wanted to record the time taken to see the second picture after seeing the first. However in their pilot study they found that many people could not be bothered trying to see the other picture or took so long that they gave up. Hence the investigators decided simply to record whether the subjects were interested in trying to see the other picture. In conducting any type of investigation (most commonly a survey) that requires cooperation of subjects, care or compromise is often required to ensure consistency of circumstances and quality (for example, accuracy) of data.
The pilot study also revealed to the investigators that they needed to decide as a group how to show the picture and what to ask, and to ensure consistency in their approach. A brief explanation was given to each subject before showing the picture, namely, “I’m going to show you a picture that could be seen as a picture of an old man or of a young man. Tell me as soon as you’ve seen either the old or young man, and which one you see.”
Another aspect requiring planning and a decision occurs whenever dominant hand (that is, right- or left-handed) is one of the variables desired to be included in the study, not only because this can be defined in a number of ways, but also because some people may have chosen, or been encouraged, to modify or, alternatively, develop, their natural behaviour. One possibility is to ask if a subject uses their left hand for any activity such as writing, throwing, using a racquet or bat, etc; this is recording any left-handed tendencies. As always, the important aspect for a data investigation is clear description of the variables, data collection and circumstances.
In this module, we consider only the variables time to see the picture and which picture was seen.
Example C: Gogogo!
The students in this group were interested in investigating whether speed of approaching traffic lights tended to be different for green or amber traffic lights and whether this was affected by driver gender, age or vehicle type, colour or make. Because they needed to observe unimpeded traffic in approaching lights, they chose their time and place carefully. They chose to take observations on a Saturday at a time when traffic was not heavy, and they chose a multi-lane one-way street with a left hand turn only lane and another one-way street crossing it so that no right turns were possible and any vehicles turning left did not impede traffic travelling straight ahead. They recorded data only for vehicles that had free approach to the lights − that is, not impeded in any way by other vehicles. To collect information on speed, they recorded the time in seconds that vehicles took to pass through a 50 metre section just before the set of lights. They also recorded gender and (broad) age group of driver, and colour, type and make of vehicle.
In this module, we consider only the time to travel the 50 metre section (in seconds) and the colour of the lights.
Example D: dissolving times for soluble aspirin
Students interested in chemistry decided to investigate the time to dissolve different types of soluble aspirin tablets, as the type of substances mixed with the aspirin differ across brands and types of tablets. An experiment was conducted with 5 brands, using two water temperatures (room/fridge but controlled to exact temperature settings), and two pH’s of water (neutral/acidic, again controlled to be exact selected pH values). A practical challenge was deciding when the tablets would be classified as “dissolved”. For their experiment, they decided the aspirin would be classified as dissolved once the tablet had broken up and dissociated from the surface of the water.
The same amount of water was used each time, and the temperatures and pH’s controlled carefully using the same instruments to measure these. The investigators decided not to use stirring as it was too difficult to control consistency of stirring.
It was decided to apply each of the 20 (5 × 2 × 2) combinations of experimental conditions three times. Hence 12 tablets of each brand were required. These were chosen randomly from larger packets, and the order of application of experimental conditions was randomised. The experiment was carried out on one day in one room with constant air temperature.
Example E: The flight of paper planes
This student group investigated variables that might affect the distance and the flight time of different designs and materials of paper aeroplanes. The experiment was conducted in an enclosed space to minimise the influence of the weather. Three different plane designs were made using three different types of paper (rice, plain and cartridge), and each combination was thrown four times by each of four different throwers. For each throw, the flight time, distance, type of landing (nosedive/glide), position on landing (upright/not) and whether there had been any obstacles, were all recorded. All flights took place on the same day in the same location. The order in which the planes were thrown was randomised.
In this module, the flight times and the design and paper type will be considered.
Example F: Body statistics
The students conducting this investigation were interested in a variety of body measurement data and the person’s ability to perform unique body-related skills (touching toes, touch nose with tongue, curl tongue). They took nine different body measurements as well as recording gender and age and the three body-related skills. In this module, we will consider only head circumference (measured around eyebrows, in cm), shoulder width (shoulder tip to shoulder tip, in cm) and gender.
Histograms and stem-and-leaf plots
For quantitative data, students have seen dotplots which plot the raw data with a “dot” for each observation, unless there are large numbers of observations when each “dot” might represent two observations.
For continuous data, and count data with many different counts, students have seen (in Year 7) stem-and-leaf plots which present the data as frequencies in equal-sized intervals, but retaining the information of the actual values, although these might need to be restricted to two or three significant figures.
Presenting continuous data as frequencies (or relative frequencies) in intervals is not only appropriate because continuous variables take values in intervals (as explained above), but also because such plots provide a smoother picture of how the data are behaving over the (continuous) range of possible values of the variable.
Another plot often used for continuous data (or count with many different values) that also presents the data as frequencies (or relative frequencies) in intervals, is a histogram. To draw a histogram, we divide the range of the data into intervals that are (usually) equal, group the continuous data into these intervals, and the plot consists of connected boxes, called bins, over the range of the data, with the size of a bin representing the frequency (or relative frequency) of observations that fall in that bin. If the range is divided into intervals of equal length, then the heights of the bins represent the frequencies (or relative frequencies) of observations that fall in the intervals marked by the bins. This is why we almost always choose to divide the range of the data into equal intervals. Whether we use frequencies or relative frequencies, the shape of the histogram is the same, as only the scale of the vertical axis is affected. We tend to plot frequencies in histograms so that we can also see how many observations we have in total.
The choice of actual starting and ending values overall for a histogram is free, as is the choice of number of intervals into which to divide this overall distance. There are no fixed rules or guidelines for choice of number of intervals − and hence number of bins, as almost all datasets will have some bins with only a few observations and others with considerable numbers. Too many bins can mislead the viewer as there will be many “bumps” in the data; too few bins can hide features of the data because of too much “smoothing”. But whatever the choices of the bins and the actual starting and end values, it must be remembered that the same dataset can look quite different for different choices.
So both stem-and-leaf plots and histograms group continuous data into intervals and present the frequencies of observations in the intervals. Stem-and-leaf plots retain information on the actual values of the observations, but the intervals starting points and the lengths of the sub-intervals are restricted. Histograms do not retain information other than frequencies of observations in intervals, but the choice of starting points for the intervals and the lengths of the intervals is not restricted (except by avoiding too many or too few intervals).
Below are a stem-and-leaf plot and three histograms with different numbers of bins or different starting values, of the same dataset of 48 observations.
|
Leaf unit = 1.0 |
||
| 0 | 4 | |
| 0 | 78889 | |
| 1 | 111224 | |
| 1 | 55666667799 | |
| 2 | 233333444 | |
| 2 | 5789 | |
| 3 | 334 | |
| 3 | 5789 | |
| 4 | 00 | |
| 4 | 88 | |
| 5 | 3 |
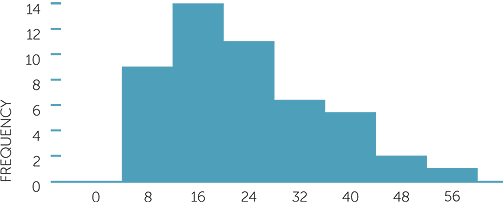
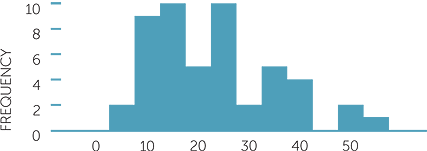
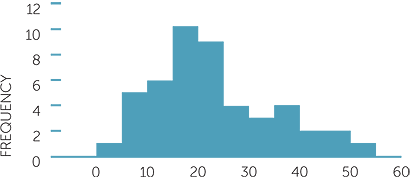
Which histogram gives the same picture as the stem-and-leaf plot?
We see how much the picture provided by the histogram of the same dataset depends on the choices of number of bins and on starting values for the intervals. Which gives the best picture of the data? The first histogram is probably the smoothest while still capturing key features of the data. The third histogram is also reasonably smooth, but notice that it has the same number of bins as the second so any particular dataset may require trying a couple of histograms to see which is a better picture of the data.
The above example also illustrates the importance of allowing for variability in the data as well as emphasizing that commenting on histograms must be done with great caution.
Introducing concepts of shape of data
The average of the 48 observations in the plots above is 22.77 and the median is 22.5. Reminder: the median is readily obtained from the stem-and-leaf plot as it is halfway between the 24th and the 25th observations once they are ordered from smallest to largest, so it is halfway between 22 and 23.
So there is not much difference between the average and the median, and either gives a reasonable measure of centre of the data. How do the data compare on each side of the average/median? On the lower side of the “centre” the values are more squashed together than on the upper side. Using the median as “centre”, the lower half of the observations range over 18 values, from 4 to 22, while the upper half range over 30 values, from 23 to 53. We can see easily in the stem-and-leaf plot and two of the histograms above, that the upper half of the data are considerably more spread out than the lower half of the data.
If the average and median are very close together and if the upper half of the data look reasonably close to a mirror image of the lower half of the data reflected around the centre, then we say that the data appear to be reasonably symmetric. Notice that because we are dealing with data, we have to allow for variation, so we will never get exact mirror images.
If the upper half of the data does not look like an approximate mirror image of the lower half, we say the data appear to be asymmetric. If the average and median are quite different, this will almost certainly be the case, but even if the average and median are not particularly different − as in the above example − the data can be asymmetric. If one half of the data are clearly more spread out than the other half, we say the data are skew. In the above example, the upper half of the data is more spread out than the lower half. Such data are said to be skew to the right. If the lower half of the data is more spread out than the upper half, we say the data are skew to the left.
In the stem-and-leaf plot and two of the histograms above, the frequencies of the intervals tend to increase to the centre and then gradually decrease. Such data are often called unimodal. But for the same data, one of the histograms does not look like this − its frequencies increase, decrease for one bin, then jump up again before falling low again and increasing slightly before dropping down again. If this is the only plot of the data considered, then a viewer might be tempted to think that there is more than one type of group in these data, and might be tempted to call the data bimodal − which means having two groups with larger frequencies than the groups on either side of them − or even tri-modal! As you can see from the above example, such a description could be very misleading. Generally speaking, continuous data (and indeed, data in general) should not be described as unimodal or bimodal or any-modal unless it is so obvious that any grouping of the data in histograms or stem-and-leaf plots shows that there are two or more groups in the data. For example, if your data consisted of heights of children and heights of adults, you would expect to get plots that looked bimodal, but why would anyone think of looking at such data in one plot?
Generally speaking, do not be tempted to use the term bimodal in looking at plots of continuous data unless a number of different grouping arrangements of the data (in histograms or stem-and-leaf plots) all indicate that there are two different groups within the data with respect to the variable being plotted.
Comparing quantitative data across categories
Data on the continuous variable (or count data with many different values) of some of the above examples are now explored across one or two of the categorical variables, using stem-and-leaf plots, and/or histograms, and sample means, medians and ranges. When using plots to compare data across categories, the same scale must be used.
Example A: How often do people blink?
Below are histograms of the number of blinks per minute for males and females separately. Number of blinks per minute is a count variable, but because there are many different values, we can use plots such as histograms and stem-and-leaf plots. Note that the histograms are on the same scale.
histogram of No. of blinks
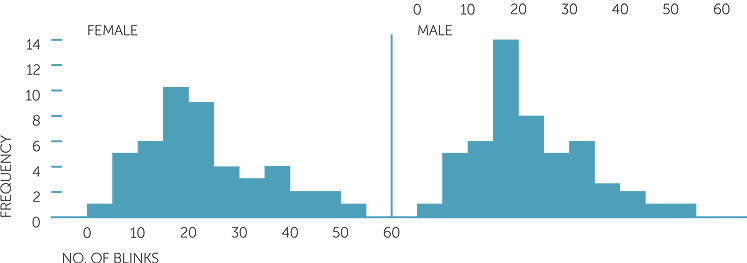
The summary statistics for the males and females for number of blinks per minute are that there are 53 males with an average of 21.77 and a median of 19 blinks per minute, and 48 females with an average of 22.77 and a median of 22.5 blinks per minute. (The data for the females is the dataset considered above). The observations for the males range from 2 to 50 and for the females, from 4 to 53.
Hence there is very little difference between the males and females − both groups have similar averages and medians and similar ranges. The histograms are also reasonably similar shapes (note that there are more males than females), and both appear to be skew to the right − that is there is more variability amongst subjects who blink most.
Below are histograms of the number of blinks per minute for male and female observers separately. Note that the histograms are again on the same scale.
The summary statistics for the male and female observers for number of blinks per minute of their subjects are that there are 51 female observers with an average of 25 and a median of 24 blinks per minute for their subjects, and 50 male observers with an average of 19.44 and a median of 17 blinks per minute for their subjects. The observations for the female observers range from 2 to 53 and for the male observers, from 4 to 50.
histogram of No. of blinks
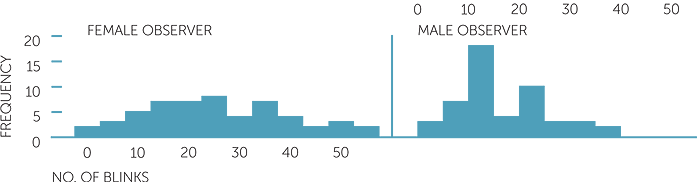
Hence there seems to be quite a difference in the number of blinks per minute of subject depending on whether they were interviewed by a male or a female, remembering that the two pairs of collectors consisted of an interviewer and an observer and the two pairs were both females or both males. The number of blinks per minute tended to be generally greater and more variable for the female interviewer than the male interviewer. Could this be due to the way the interviewer asked the questions or a difference in response to male and female interviewers?
A question that immediately arises is whether the different combinations of interviewer and subject genders show any effects. Below are histograms of the number of blinks per minute with the data divided into the 4 groups formed by these different combinations.
We see that there is not much difference between female and male subjects with male interviewers, and that for female interviewers, the male and female subjects tend to have similar ranges of values, but that the values for female subjects tend to be skew to the right, while those for the male subjects are more symmetric.
histogram of No. of blinks
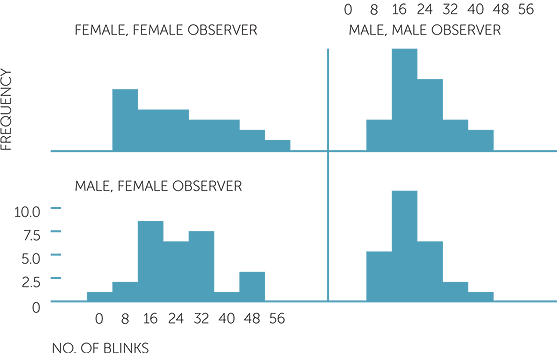
We can also use stem-and-leaf plots on the same scale to explore these data. To do this, it is useful to use what are called back to back stem-and-leaf plots to facilitate a comparison between two sets of quantitative data on the same scale. Although only two groups can be put on a back to back stem-and-leaf, judicious use of them can be useful. For example, in this example, we are now focussing on comparisons between female and male subjects for each of female and male interviewers, because we have seen that there is little difference overall between female and male subjects, but there does appear to be differences due to interviewer gender.
Below are back to back stem-and-leaf plots of the number of blinks for female subjects split by gender of interviewer, and for male subjects, split by gender of interviewer.
|
Leaf unit = 1.0 |
||||
| Female subject, male observer | Female subject, female observer | |||
| 0 | 4 | |||
| 0 | 78889 | |||
| 22111 | 1 | 4 | ||
| 77666655 | 1 | 699 | ||
| 443333 | 2 | 234 | ||
| 95 | 2 | 78 | ||
| 43 | 3 | 3 | ||
| 7 | 3 | 589 | ||
| 0 | 4 | 0 | ||
| 4 | 88 | |||
| 5 | 3 | |||
|
Leaf unit = 1.0 |
||||
| Male subject, male observer | Male subject, female observer | |||
| 0 | 2 | |||
| 8665 | 0 | 7 | ||
| 4441 | 1 | 133 | ||
| 97776655 | 1 | 567889 | ||
| 43221 | 2 | 234 | ||
| 6 | 2 | 5568 | ||
| 21 | 3 | 0244 | ||
| 8 | 3 | 55 | ||
| 4 | 24 | |||
| 4 | 7 | |||
| 5 | 0 | |||
These illustrate that the biggest contrast between the effects of male and female interviewers on the subjects is that the variation in number of blinks per minute is much smaller for male interviewers than for female interviewers.
Example B: optical illusions
Below are histograms, back to back stem and leaf plots and summary statistics on the time to see a picture in secs and which picture was seen (old or young man).
histogram of time to see in secs
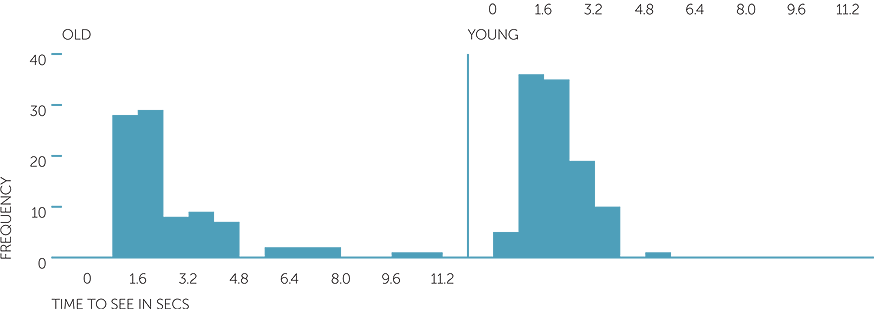
|
Leaf unit = 0.1 |
||||
| Time to see young man | Time to see old man | |||
| 9998887765 | 0 | 8999 | ||
| 4443333322221111111110000 | 1 | 0000001112222333444 | ||
| 999988887777666666655555 | 1 | 55555666666778888899999 | ||
| 443333222222221110 | 2 | 001111122334 | ||
| 99998877555555 | 2 | 5669 | ||
| 44432100 | 3 | 001333 | ||
| 99555 | 3 | 555578 | ||
| 2200000 | 4 | 002234 | ||
| 5 | 4 | 7 | ||
| 5 | ||||
| 5 | 68 | |||
| 0 | 6 | |||
| 6 | 59 | |||
| 7 | ||||
| 7 | 55 | |||
| 8 | ||||
| 8 | ||||
| 9 | ||||
| 9 | ||||
| 10 | 04 | |||
For the 113 people who saw the picture of the young man first, the average time to see the picture was 2.15 secs and the median was 1.95 secs, while for the 89 who saw the picture of the old man first, the average time to see the picture was 2.64 secs and the median was also 1.95 secs. The times to see the young man ranged from 0.59 to 6 secs, while the time to see the old man ranged from 0.89 to 10.4 secs.
From the histograms and the stem-and-leaf plots and the summary statistics, we see that generally there was little difference in times to see between seeing old or young man, with most subjects seeing a picture within 5 secs, and with no difference in the median time, but that those who took longer to see a picture tended to see the old man, and so the times to see the old man were much more skew to the right than the times to see the young man.
Example C: Gogogo!
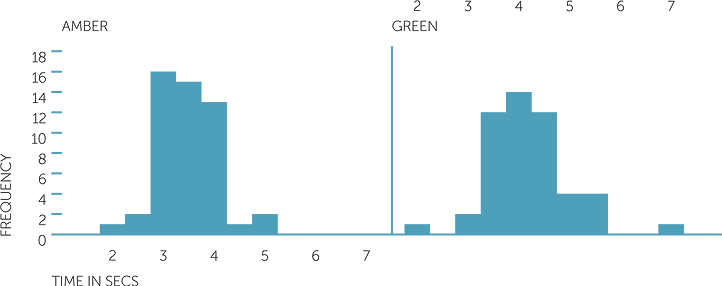
Below are histograms on the same scale and back to back stem-and-leaf plots for the time in seconds to travel the last 50 metre section and the colour of the lights.
histogram of time to see in secs
|
Leaf unit = 0.1 |
||||
| Green | Amber | |||
| 0 | 2 | 03 | ||
| 2 | 67778899999 | |||
| 33311 | 3 | 001111223334 | ||
| 9999877777666555 | 3 | 5555556777778899999 | ||
| 443321111000 | 4 | 111 | ||
| 8777666555 | 4 | 779 | ||
| 321 | 5 | |||
| 65 | 5 | |||
| 6 | ||||
| 8 | 6 | |||
The average time to travel the last 50 metres approaching amber lights was 3.44 secs and the median time was 3.48 secs, while for approaching green lights, the average was 4.17 secs and the median was 4.1 secs. The times for approaching amber lights ranged from 2 secs to 4.9 secs and for green lights, from 2 secs to 8.6 secs.
Hence we see that the time to approach amber lights was generally less than for approaching green lights. Apart from two extreme values in approaching green, the variability (or spread) of the times is not very different between amber and green. The times to approach amber lights were fairly concentrated and not particularly skew, while the times to approach green lights could be described as slightly (but only slightly) skew to the right.
Example E: The flight of paper planes
Below are histograms and summary statistics for the flight times in seconds for the different designs and for the different paper types.
histogram of flight time
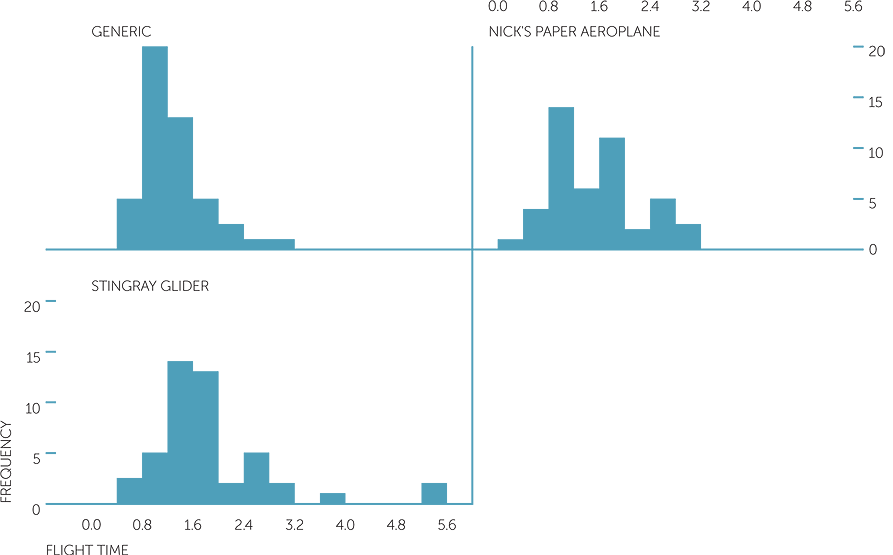
The average flight times for the generic, nick’s and stingray designs were, respectively, 1.3 secs, 1.56 secs, 1.8 secs, and the median times were, respectively, 1.15 secs, 1.5 secs, 1.66 secs. We see that the stingray design had a few considerably longer flights (and so skew to the right) and tended to have slightly longer times than the other two, and that the generic design’s times tend to be slightly shorter than Nick’s design and less variable.
histogram of flight time
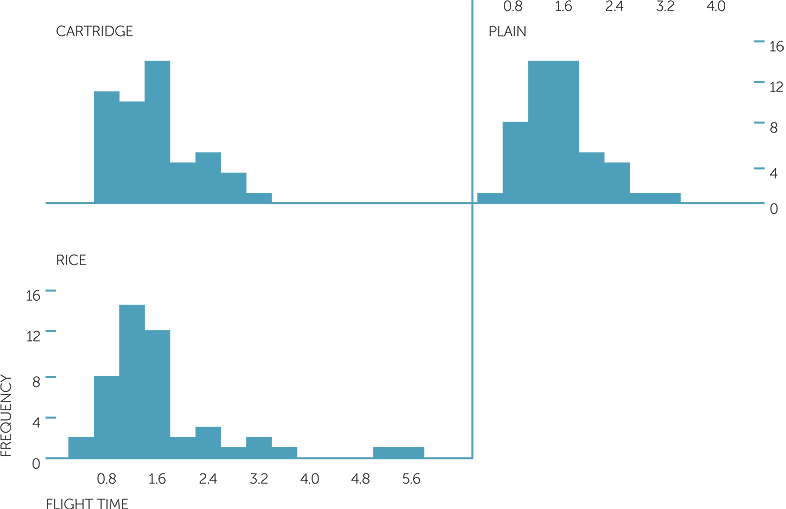
The average flight times for the cartridge, plain and rice papers were, respectively, 1.54 secs, 1.5 secs, 1.66 secs, and the median times were, respectively, 1.5 secs, 1.4 secs, 1.3 secs. We see that all three groups are skew to the right. The rice paper had a few considerably longer flights but otherwise did not tend to have longer times than the other two. There’s not a great deal of difference between the three papers.
A question that immediately arises is whether some papers suit some designs better than others. Below are stem-and-leaf plots for the flight times for the different papers for each design. Note that although we cannot do back to back stem-and-leaf plots for three groups, the plots are on the same scale.
|
Leaf unit = 0.1 |
||||||||
| generic, plain | generic, rice | generic, cartridge | ||||||
| 99877 | 0 | 9999 | 0 | 6778888 | ||||
| 32100000 | 1 | 34444 | 1 | 00123444 | ||||
| 66 | 1 | 569 | 1 | 9 | ||||
| 1 | 2 | 134 | 2 | |||||
| 2 | 2 | |||||||
| 3 | 0 | 3 | ||||||
|
Leaf unit = 0.1 |
||||||||
| Nick’s, plain | Nick’s, rice | Nick’s, cartridge | ||||||
| 0 | 3 | 0 | ||||||
| 7 | 0 | 89 | 0 | 6679 | ||||
| 410 | 1 | 000001122 | 1 | 0024 | ||||
| 97766 | 1 | 5 | 1 | 666677 | ||||
| 311 | 2 | 2 | 0 | |||||
| 655 | 2 | 59 | 2 | 6 | ||||
| 0 | 3 | 1 | 3 | |||||
|
Leaf unit = 0.1 |
||||||||
| Stingray, plain | Stingray, rice | Stingray, cartridge | ||||||
| 0 | 4 | 0 | ||||||
| 875 | 0 | 99 | 0 | |||||
| 42211 | 1 | 022234 | 1 | 33 | ||||
| 9766655 | 1 | 6677 | 1 | 556789 | ||||
| 2 | 2 | 2344 | ||||||
| 5 | 2 | 2 | 579 | |||||
| 3 | 3 | 0 | ||||||
| 3 | 7 | 3 | ||||||
| 4 | 4 | |||||||
| 4 | 4 | |||||||
| 5 | 2 | 5 | ||||||
| 5 | 5 | 5 | ||||||
We see that it doesn’t seem to matter which paper is used for the generic design; that for Nick’s design, the plain paper may be preferable but the rice paper is capable of occasional longer times; and that for the stingray design, the cartridge paper is generally better although again the rice paper can give unusually longer times.
Example F: Body statistics
Below are histograms of head circumference (measured around eyebrows, in cm), and shoulder width (shoulder tip to shoulder tip, in cm) split by gender.
histogram of head
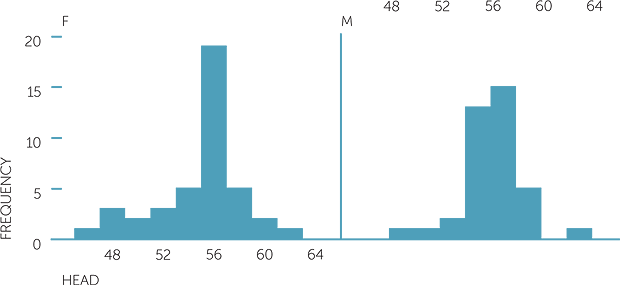
We see that for both females and males, the head circumferences tend to be skew to the left. There is not as much difference between males and females as one might expect, but the females’ circumferences tend to be more variable.
histogram of shoulders
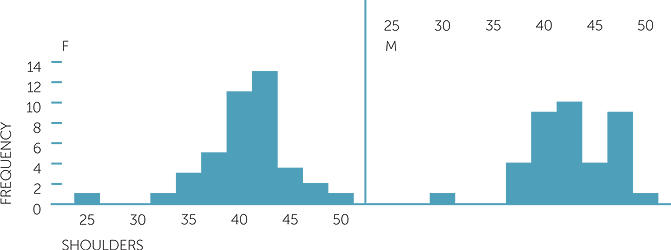
For the shoulder widths, apart from one unusually small female, the females’ shoulder widths are quite symmetric, ranging from about 32 to 52 cm and concentrated around approximately 42 cm, while the males’ shoulder widths (apart from a smaller value) are fairly evenly spread over approximately 38 to 58 cm.
Summarising techniques for collecting data
In Year 8, students considered censuses, surveys and observational investigations. In the examples above, we also see examples of experimental data investigations.
The type of data collection, in which the aim is to collect information about every member of a population, is called a census. Datasets that are not census data are often called samples of data. The general meaning of the word “sample” is a portion, piece, or segment that is representative of a whole. In statistics, a sample of data, or a data sample, is a set of observations such that more, sometimes infinitely more, observations could have been taken. We want our sample of data to be randomly representative of some general situation or population so that we can use the data to obtain information about the general situation or population. A particular dataset might be considered to be randomly representative for some questions or issues, but not for others.
Census
We mostly associate the word “census” with the censuses carried out by national statistical offices, such as the Australian Bureau of Statistics. These censuses are major undertakings conducted to obtain as complete information as possible on variables that are important for government, industry and the whole community. National censuses aim to obtain population data not only for vital information for future planning and strategies, but also to guide further data collections.
Australia conducts a national census approximately every five years. It is called the Census of Population and Housing. The date of the 16th Australian Census is 9th August, 2011.
The word “census” comes from the Latin, censere, which means “to rate”, and an essential and first aim of a country’s census is to count − total number of people and numbers in different groupings. This is partly why a census is of the whole population.
It is very important for nations to have accurate census data. The quality of Australia’s census data is highly regarded internationally. What can go wrong in collecting census data? There are many challenges: ensuring everyone is reported on one and only one census form, ensuring every census form is completed and returned, omissions, accidental errors, errors due to language or understanding difficulties, deliberate errors. National offices of statistics use many sophisticated statistical techniques to estimate and cross-check for errors, and to “allow for” the types of challenges outlined above.
Collecting data for data investigations
In Year 8, there is considerable focus on the practicalities of obtaining randomly representative data using surveys or observational studies (or a mixture). By randomly representative data we mean a set of observations obtained randomly in circumstances that are representative of a more general situation or larger population with respect to the issues of interest. The randomness is important as it allows us to infer from the sample of data to the more general situation or larger population with respect to the issues of interest.
Surveys and observational studies require care, sometimes great care, in their design, the practical challenges of their implementation, and their interpretation. In all reporting of data investigations it is of critical importance to clearly describe how the data were collected so that readers and users of the report and results can understand or perhaps critique in what way we can consider the data to be randomly representative of more general situations.
In the examples above, we see examples of experimental data investigations, in which the investigator sets up experimental conditions, controlling the conditions and collecting observations on the response to those conditions. In experimental data investigations, once the combinations of controlled conditions are designed, it is very important to randomly allocate subjects (whether the subjects be people or laboratory specimens or plants etc) to each combination of controlled conditions.
The three main types of data investigations are surveys, observational studies and experiments, but many real data investigations can be considered as having a combination of these elements.
Example A investigating how often people blink could be considered as a combination of experiment and observation. Some of the conditions are controlled but some (such as gender and whether subjects wear glasses) are not, and the subjects are chosen as randomly as possible.
Example B investigating whether people see the old or young man could be considered a combination of observational study and survey.
Example C investigating approach to traffic lights is an observational study, but note that investigators must select conditions for it.
Example D investigating solubility of aspirin is an experimental data investigation.
Example E investigating flights of paper aeroplanes is an experimental data investigation.
Example F investigating body statistics is a survey but has elements of observational study in it.
Hence classifying types of data investigations are useful in understanding practical challenges, but are not necessarily clear-cut.
Links from F-8 and towards year 10
From F-8, students have gradually developed understanding and familiarity with concepts and usage of the statistical data investigative process, types of data and variables, types of investigations and some graphical and summary presentations of data appropriate for the different types of data. Students have planned and carried out data investigations involving different types of variables and used a variety of graphical and summary presentations of data to explore and comment on features of data in relation to issues of interest. In Year 6 they have considered questions or issues involving two or more categorical variables, exploring how data from one categorical variable may be affected by another. In this module for Year 9, students have extended these concepts and experiences to data investigations involving at least one quantitative (mostly continuous) and at least one categorical variable, and used plots on the same scale and the summary statistics of mean, median and range to explore and comment on features of quantitative data across categories of a categorical variable. Another plot for continuous data, the histogram, has been introduced to assist in such investigations, and the concept of stem-and-leaf plot extended to considering back to back stem-and-leaf plots. Some concepts of shape of data have also been introduced to assist in describing features of data.
Throughout Years 1-8, in considering more and more aspects of data investigations, students have experienced and discussed the challenges of obtaining randomly representative data, with emphasis on the importance of clear reporting of how, when and where data are obtained or collected, and of identifying the issues or questions for which data are desired to be randomly representative. In Year 8, students used real data and simulations, including re-sampling from real data, to illustrate how sample data and data summaries such as sample proportions and averages can vary across samples. The concepts explored in Years 7 and 8 of the effects of sampling variability and of describing and/or allowing for variability within and across datasets, have been an important part of learning to comment on data in Year 9.
In exploring the practicalities and implications of obtaining data in Year 8, students developed understanding of the nature of censuses, surveys and observational studies. Year 9 has developed this understanding further, and has introduced examples of experimental investigations with emphasis on random allocation of the combinations of experimental conditions.
Experiments provide a natural context for comparisons of continuous data across categories of categorical variables, and these comparisons have been the focus of Year 9. Year 10 continues this theme, introducing box plots as another graphical tool for such comparisons. From this focus on relationships between continuous and categorical variables, Year 10 then moves to consider using scatterplots to explore relationships between continuous variables, including examples involving time, and examples available in digital media.
As in Years F-8, concepts are introduced, developed and demonstrated in contexts that continue the development of experiential learning of the statistical data investigation process. The examples continue to illustrate the extent of statistical thinking involved in all aspects of a statistical data investigation, including identifying the questions/issues, in planning and in commenting on information obtained from data.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

