The Improving Mathematics Education in Schools (TIMES) Project
Data Investigation and interpretation
Statistics and Probability : Module 2![]() Year : 4
Year : 4
June 2011
It is assumed that in Years F-3, students have had learning experiences involving choosing and identifying simple questions from familiar situations that involve gathering information and data in which observations fall into simple, natural categories. It is assumed that students have had learning experiences in recording, classifying and listing such data, and have seen and used tables, picture graphs and column graphs of categorical data with simple, natural categories.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and demands for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
A natural environment for learning statistical thinking is through experiencing the process of carrying out real statistical data investigations from first thoughts, through planning, collecting and exploring data, to reporting on its features. Statistical data investigations also provide ideal conditions for active learning, hands-on experience and problem solving. Real statistical data investigations involve a number of components:
- formulating a problem so that it can be tackled statistically;
- planning, collecting, organising and validating data;
- exploring and analysing data; and
- interpreting and presenting information from data in context.
A number of expressions to summarise the statistical data investigative process have been developed but all provide a practical framework for demonstrating and learning statistical thinking. One description is ‘Problem, Plan, Data, Analysis, Conclusion (PPDAC)’; another is ‘Plan, Collect, Process, Discuss (PCPD)’.
No matter how it is described, the elements of the statistical data investigation process are accessible across all educational levels.
In this module, we consider, in the context of statistical data investigations, data
where each observation falls into one of a number of distinct categories. Such data
are everywhere in everyday life. Some examples are:
- gender
- direction on a road
- type of dwelling
Data of this type is called categorical data.
Sometimes the categories are natural, such as with gender or direction on a road,
and sometimes they require choice and careful description, such as type of dwelling.
Another type of data situation in which each observation falls into one of a distinct number of categories is count data. Each observation in a set of count data is a count value. Count data occur in considering situations such as:
- the number of children in a family
- the number of children arriving at the tuckshop in a 5 minute interval
- the number of taxis waiting at a taxi rank at a selected point of time
- the number of TV sets owned by a family.
Count data in which only a small number of different counts are observed can also be treated as categorical data, particularly for the purposes of data presentations.
This module considers statistical data investigations involving categorical data and count data. In the situations described in this module count data is treated as categorical data because of it involving a small number of different values of counts.
The focus in the exploration and interpretation phases is on data with just one set of categories, even if the questions or issues of interest involve more than one possible set of categories. That is, a topic of interest may involve both type of dwelling and number of pets in a family, but in exploring and interpreting, this module focuses on each of these in turn.
This module uses three examples to develop the statistical data investigation process through the following:
- considering initial questions that motivate an investigation;
- identifying issues and planning;
- collecting, handling and checking data;
- exploring and interpreting data in context.
The phases lend themselves to representation on a diagram, as follows.
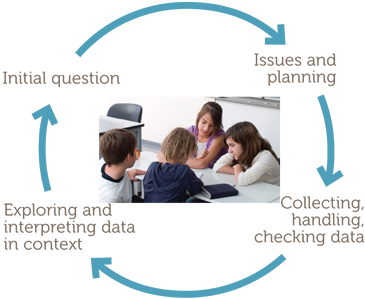
Initial questions that motivate an investigation
The following are some examples of questions that involve collecting and investigating categorical data or data involving a small number of different values of counts.
- A
- Do you have a pet? What type of pet is it? Is the pet yours or a family pet?
Does your family have more than one pet? How many pets do families tend
to have? Are cats more popular than dogs? - B
- What colours of cars tend to be in your neighbourhood? Are there big cars or small cars? What are the most popular colours for cars? Grey has become a very popular colour for cars − is it more popular than white?
- C
- How many different colours are there in Smarties or M&M’s? What is your favourite colour? Do packets of Smarties or M&M’s tend to contain about the same number of each colour?
These are examples of just some of the many questions that can arise involving categorical data. These questions are used here to explore the progression of development of learning about data investigation and interpretation.
General statistical notes for teachers
Identifying and describing categories
Categorical data are data in which each observation falls into one and only one category. The categories are usually natural categories such as cat or dog, male or female, but often there are many possible categories or different possible descriptions. If so, we need to carefully choose our groupings and descriptions of them. Colour is usually categorical unless we are being scientific and describing colour by a scientific measure. In Example C above, the colours are chosen and fixed for us. However, in Example B, the investigators will need to decide what colour groupings they are going to use and describe these carefully so that the data collected are consistent and reliable. The description must also be clear for anyone listening to, or reading, a report of the investigation.
Some categorical data need careful description of their categories. For example, period of a day could be described as peak or off-peak; day or night; morning, afternoon, evening, night. A person’s age group could be described as child, teenager, adult. These examples also illustrate that many sets of categorical data come from creating or imposing categories for data such as time or age (which is itself time of course).
General statistical notes for teachers
Count data
Each observation in a set of count data is a count value. Hence count data occur only in situations such as observing the number of children in a family, the number of TV sets owned by each family. Note that age does not a give count data because it has units (years or months or weeks or days etc).
Some count data sets have many different observed values, such as number of people at football matches collected over a season, but some have only a few different observed values, such as number of dogs owned by city-dwelling families. Count data with only a few different observed values are often presented using the graphs developed for categorical data.
Identifying issues and planning
In this first part of the data investigative process, one or more questions or issues begin the process of identifying the topic to be investigated. In thinking about how to investigate these, other questions and ideas can tend to arise. Refining and sorting these questions and ideas along with considering how we are going to obtain data that is needed to investigate them, help our planning to take shape. A data investigation is planned through the interaction of the questions:
- ‘What do we want to find out about?’
- ‘What data can we get?’ and
- ‘How do we get the data?’
Example A: pets
The general topic is investigating domestic or family pets. The questions above are just some that may arise in a free discussion. On the surface, this topic may seem simple but there are many aspects of it to be considered before a data investigation can be undertaken.
Some questions that need to be considered include, what sort of pets are we going to consider, and are we going to consider pets of the families with a child in Year 4 at this school, or are we going to consider more than just one class or one year level.
Students need to decide what can be called a pet even if they do not choose categories before collecting the data. For example, they may decide that a pet must be a living animal (so that pet rocks or inanimate pets are not considered) and that to be classified as a pet, an animal must be fed by the family, housed in the precinct of the family home and participate in some way with members of the family. Students living in rural or agricultural areas may need to discuss this carefully before deciding what can be classified as a pet.
Another type of consideration that comes under both identifying the issues or questions and in the planning, is on whom or what are we going to collect these data. The data are most likely collected from students, whether restricted to one class or year level or whether other classes or year levels are involved. Which 'family” to consider in the case of dual families needs to be clear. If more than one class or year level provides information, care will be needed to avoid double-counting of families with siblings at the school.
Notice that by considering pets as belonging to families, we avoid the difficulty of what would we mean by an individual student at this year level 'owning” a pet.
Next we need to consider what data we are going to collect. We could just ask for the number of pets in total, or we could ask for numbers of different types of pets, or we could simply ask for a listing of pets per family and then the students can decide how to classify the pets once the data are collected. It is likely that students will be interested in the various types of pets of the families of their classmates, so a listing of pets per family may be the best raw data to collect.
Example B: cars
The general topic is colour of cars. As with pets, there are many aspects of this topic that need discussion and decisions. The first is, what do we mean by a 'car”? Are we going to include all types of vehicles or not consider trucks, buses, motor bikes etc? This is up to the students and their teacher − the important point is to make sure that those collecting the data are clear about what to observe and that it is described clearly in any reporting.
We need to decide where we are going to collect the data. They could be collected by observation of cars passing the school, or of cars parked in a large carpark, or by a survey of students reporting the colour of the car or cars owned by their family. Only one of these ways should be used to avoid doubling counting (or even triple counting!) and each way may or may not represent slightly different general situations. This last point can be raised even at such early stages of development.
Colour of cars is not straightforward, and, unlike the pet example, how to record colours must be worked out before the data are collected in order to obtain consistent data. Although there might be many opinions offered by students, at this early stage of development, some simple classifications could be selected, such as: white; black; grey or silver; all reds, yellows, browns; all blues, greens, purple.
Example C: m&m’s or smarties
The general topic is colour of Smarties (or M&M’s). This is the simplest of the three examples here from the point of view of what to observe. The same type of sweet would be observed (e.g. not peanut ones) and the colours are set by the manufacturer. One decision that is needed is what size packet to buy and whether to look at colours in each packet with a number of different packets or whether just to look at one large number of sweets. However comparing summaries of colours observed over different packets of the same size provides an introduction to concepts of variation over samples − in this case, samples of sweets. In this example, the colours could be recorded separately for each packet and then the data could be combined overall.
General statistical notes for teachers
Each of the above examples demonstrates key statistical aspects of the initial phases of data investigations in illustrating
- how initial ideas lead to questions to be investigated which then lead to identification of what is to be collected or observed
- identification of the ‘subjects’ − on what will the data be observed or collected
- early considerations of what the data represent.
Planning a statistical investigation involves identification of what is to be observed (what data are we going to collect) and the ‘subjects’ or ‘experimental units’ of the investigation − that is, on what are we are going to collect or observe our data?
The ‘what’ we are going to observe is called a statistical variable.
In Example B, the ‘subjects’ are cars, and the variable of interest is ‘colour of car’. We could summarise our plan by the sentence, ‘The cars passing the school will be classified by their colour’.
In Example C, the ‘subjects” are individual sweets, and the variable of interest is colour of the sweet. We could summarise our plan by the sentence, 'Each sweet in a packet of M&M’s will be classified by its colour”.
Collecting, handling and checking data
Example A: pets
For the example on pets, if the data are collected by listing all pets, the recording form might look like this:
| Student name | Family name | Pets |
| Abigail | Jones | Dog, 2 birds |
| Fred | Smith | 2 mice, tortoise |
| Jenny | Nguyen | Cat |
If the classifications of pets are chosen before the data are collected, the recording form might look like this:
| Student name | Family name | Dogs | Cats | Birds | Other |
| Abigail | Jones | 1 | 0 | 2 | 0 |
| Fred | Smith | 0 | 0 | 0 | 3 |
| Jenny | Nguyen | 0 | 1 | 0 | 0 |
From either form, the total number of pets for each family is readily obtained. If the data are originally collected according to the first recording form above, then how to group the data will need to be considered if it is wished to produce a table like the second above.
If the data are collected on the families of the students in the class(es) which discussed the investigation, they will be aware of the decisions of what is a pet, and what is a family. However, the students should express it in their own words for inclusion in reporting.
If the data are collected from other students or classes, the students collecting the data need to have an agreed form of words when asking other students. A trial/rehearsal of this is advisable for both confidence and consistency − and for fun!
Note that because of recording the student’s and family’s name, the number of pets of families for boys and girls in Year 4 could be considered separately if a reasonably sized dataset is collected.
Example B: colours of cars
Any data collection carried out in real time requires trialling of collection. In the case of recording colours of cars that drive past a school or other convenient location, students could work in groups of three, with one student calling out the colours and the other two, each with a recording sheet, ticking the appropriate column. If cars pass fairly frequently, some groups of students could record the cars in one direction, and other groups do the other direction. The purpose of two recorders per 'caller” and more than one group recording the same data is for checking purposes. This will illustrate to the students how easy it is to make a recording mistake.
Thus a recording sheet might look like:
| White | Black |
Grey silver |
Red yellow brown |
Green blue purple |

|
||||

|
||||

|
A preliminary 'pilot” by the students might result in change to groupings of colours.
For example, the students might want to separate red from the third grouping above.
Example C: colours of Smarties or M&M’s
Because these data are simple to collect, the recording sheet can be a final table of numbers of each colour, or students can use an intermediate stroke-and-cross recording form, such as
Green![]()

Purple ![]()
Red![]()

Each packet of sweets could be referenced by a student’s name or by an assigned number.
General statistical notes for teachers
The form of recording sheets tends to depend on the practicalities of the investigation. Usually the rows of the recording sheet correspond to the ‘subjects’.
In Example A, the ‘subjects’ are families, identified by the child who is representing the family. The second form of the recording sheet is recording the numbers of dogs, cats, birds and 'other” pets for each family. From this, the total number of pets for each family can be obtained.
In Example B, the ‘subjects’ are cars and each row of the recording sheet corresponds to a car. There is only one variable, colour, but because it is difficult to write down a colour or even a letter quickly, the recording sheet can be designed for convenience in quick recording by just requiring a tick. If this was part of a larger investigation, the data collected by the above recording sheet should be then converted to a sheet containing one column that records the colour category by name.
In Example C, the ‘subjects’ are individual sweets. The raw data would be a single column in which each sweet would be classified by its colour. Because this is tedious in this simple situation, the stroke-and-cross method can be used to bypass the raw recording sheet to go straight to obtaining the summary data.
Exploring and interpreting data
It is in exploring data that we use presentations, including graphical and summary presentations.
Categorical data are summarised by the number of observations that fall in each category. These are called the frequencies of the data − how often did each category occur. These frequencies can be presented in a table or can be graphed by a column graph in which each category has a column and the heights of the columns represent the frequency of the observations that fall in that category.
Count data are also summarised by the number of observations that fall in each category, where the categories correspond to the different possible count values that the observations take.
Thus frequency of a category is the numbers of observations in the data that fall into that category. It is frequencies that provide the information on how likely are the different categories. A similar statement for values of counts can be made.
Column graphs are also called barcharts.
General statistical notes for teachers
If count data take many different values, with frequencies of only one to three for each value, presenting the data in a table or column graph gives very little idea of what the data look like. But count data with a small number of distinct values can be presented well by using a column graph. Also, as is seen in Example A below, for count data with most observations taking only a few different values, the remaining infrequent values are often grouped together.
Example A: pets
There are a number of possible ways of considering these raw data.
The focus could be on number of pets per family, in which case the data are presented either in a table or as a column graph with frequency of families that own 0 pets, 1 pet, 2 pets etc. For example, a table of data collected from 50 families could look like this
|
Number |
0 | 1 | 2 | 3 | More than 3 |
|
Frequency |
5 | 18 | 12 | 9 | 6 |
The corresponding column graph or barchart looks like this.
Graph of number of pets
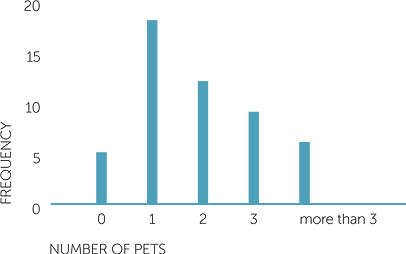
The graph shows that only 5 of the 50 families have no pets and the most common number of pets for a family to have in the data for these 50 families is 1, but more than half the 50 families have more than 1 pet.
Similarly, we could look at a particular type of pet, such as dogs or cats.
To consider the question of whether dogs are more popular than cats, are we asking if a family is more likely to own a dog than a cat? If so, each family could be classified as owning at least 1 dog but no cats, owning at least one cat but no dogs, owning both or owning neither. A possible graph of this is shown below. It shows that there is almost no difference in popularity of dogs and cats as pets for these 50 families, and that both are very popular, with more than 10 out of the 50 families owning both.
Graph of cat or dog
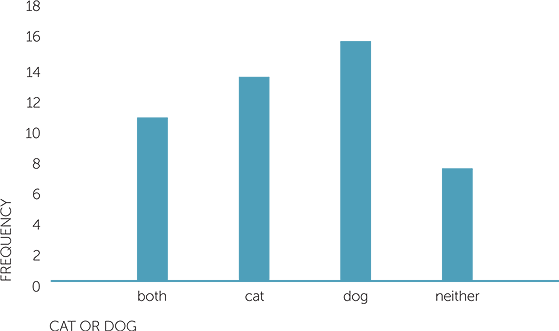
Example B: Colours of cars
From the form of the recording sheets above, it is a simple matter to obtain the frequencies of the different colours. Checks can then be made across recording sheets within each group and across groups. Differences of one or two totals for each colour are probably not worth checking, but if there are big differences, recording sheets can be compared.
Graph of colour of cars
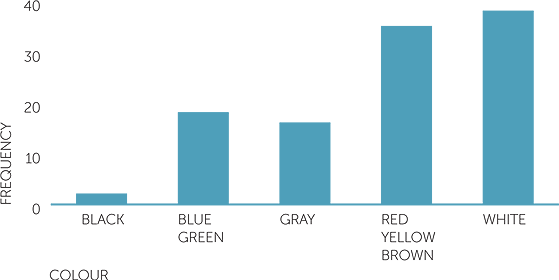
A column graph of the car colours could look like the one shown above. This shows that white is the most common colour in these data, closely followed by the group that includes red, yellow, brown. Perhaps putting all those colours in one group was not a good choice! The group of blues and greens is next but much less popular, and there were very few black cars passing on that day.
Example C: Colours of Smarties or M&M’s
As with the colours of cars, the numbers of sweets of each colour can be presented in tables or column graphs. It is easily seen how valuable the column graphs are for 'seeing” what the data are like and, in an example like this, for comparing colour frequencies in different packets of sweets. Below are column graphs of colours of M&M’s in 6 different packets. Note that the scale of the column graphs is the same so that we can easily compare the frequencies of colours within and across packets.
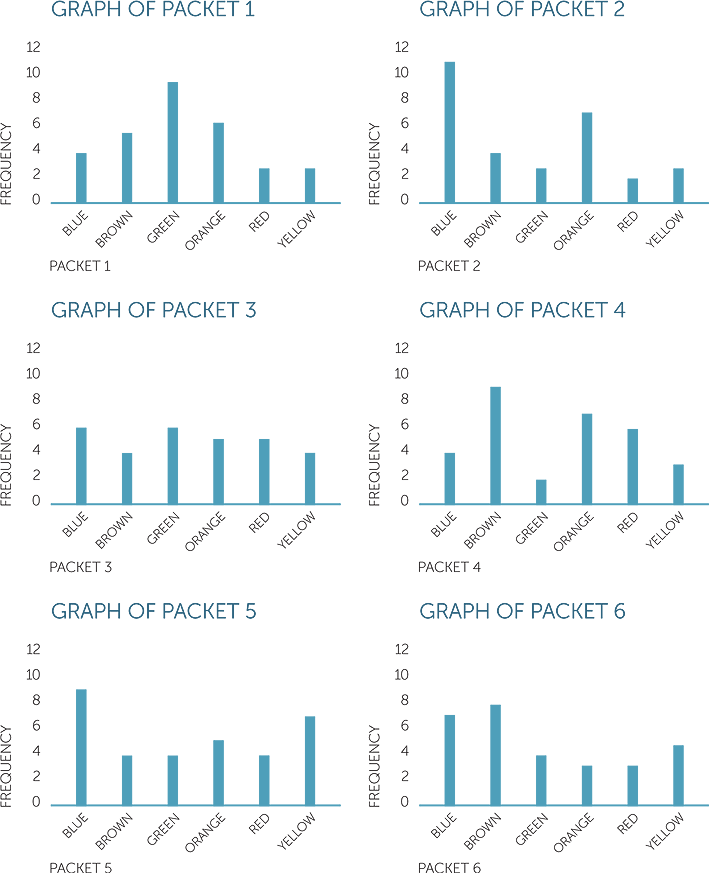
These graphs demonstrate well the amount of variation in frequencies of colours there can be across packets, even if overall the manufacturers use a fixed set of proportions of colours. [Aside: in this example, the overall fixed percentages of the different colours from which these data were obtained was: 24% blue; 14% brown; 16% green; 20% orange; 13% red; 14% yellow.]
Putting all the packets together gives the following column graph.
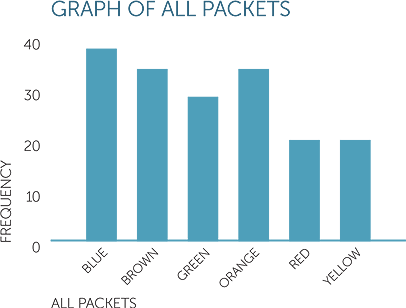
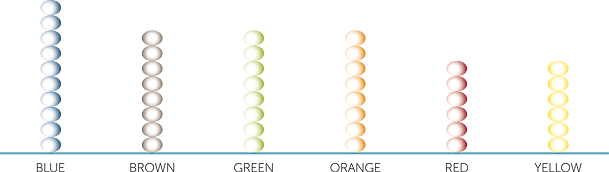
Below is a picture graph of data on colours of 180 sweets with each picture of a sweet representing 4 sweets in the data. Thus there are 40 blue sweets, 32 brown and 32 orange sweets, 28 green sweets, and 24 each of red and yellow sweets.
The students might also like to nominate their favourite colour to compare their preferences with each other and with the most frequently occurring colours in their data. Each student says their favourite colour, and a column graph presents the number of students nominating each colour.
Some general comments and
links from F-3 and towards year 5
In the above examples B and C, the variable 'colour” is a categorical variable. In Example A, the variable 'number of pets per family” is a count variable but because it mostly takes small values, it is being treated here as a categorical variable, with the last category being 4 or more pets.
Type of pet is a categorical variable, and the data in Example A could be considered as type of pet. How to treat the data in Example A depends on whether the focus is on pets in a family or on a collection of pets obtained by surveying a number of families. However it is difficult to consider what such a collection of pets would be representative of, whereas the collection of families is representative of families of Year 4 (or primary school if data collected over all year levels) in the type of region of the school.
Although simple categorical data are used in Years F-3, the above material marks the first experiences in the process of statistical data investigations. The focus has been on considering just one categorical variable at a time, so that the only types of presentations are tables and column graphs with just one set of categories. In this relatively simple situation the above examples illustrate the extent of statistical thinking involved in the initial stages of an investigation in identifying the questions/issues and in planning and collecting the data.
The three examples of the module can demonstrate concepts such as ‘what do our data represent’ and variation in data across samples. Variation in data across samples tends to arise naturally in everyday situations that are very familiar to young students. These concepts are further developed as students progress.
In Year 5, we extend the concepts of types of data to consider measurement data and more general situations with count data. In Year 5, although questions and issues may involve more than one variable, the focus is on exploring and interpreting phases of the investigation process with one variable at a time.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

