The Improving Mathematics Education in Schools (TIMES) Project
Data Investigation and interpretation
Statistics and Probability : Module 2![]() Year : 7
Year : 7
June 2011
The Improving Mathematics Education in Schools (TIMES) Project
Data Investigation and interpretation
Statistics and Probability : Module 2![]() Year : 7
Year : 7
June 2011
It is assumed that in Years F-6, students have had many learning experiences involving choosing and identifying questions or issues from everyday life and familiar situations, planning statistical investigations and collecting or accessing data. It is assumed that students are now familiar with categorical, count and measurement data, have had learning experiences in recording, classifying and exploring individual datasets of each type, and have seen and used tables, picture graphs and column graphs for categorical data and count data with a small number of different counts treated as categories, and dotplots of measurement and count data. It is assumed that focus in exploration and comment on measurement and count data has been on each set of data by itself, but that in Year 6, students have become familiar with considering more than one set of categorical data on the same subjects. In doing so, they met the concept of statistical variables and understood that they were investigating data on pairs of categorical variables. For example, if data are collected on students’ favourite TV show and favourite holiday activity, then in Year 6, the combination of data on TV shows and holiday activities are explored together using two-way tables and side-by-side column graphs.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
A natural environment for learning statistical thinking is through experiencing the process of carrying out real statistical data investigations from first thoughts, through planning, collecting and exploring data, to reporting on its features. Statistical data investigations also provide ideal conditions for active learning, hands-on experience and problem-solving. No matter how it is described, the elements of the statistical data investigation process are accessible across all educational levels.
Real statistical data investigations involve a number of components: formulating a problem so that it can be tackled statistically; planning, collecting, organising and validating data; exploring and analysing data; and interpreting and presenting information from data in context. No matter how the statistical data investigative process is described, its elements provide a practical framework for demonstrating and learning statistical thinking, as well as experiential learning in which statistical concepts, techniques and tools can be gradually introduced, developed, applied and extended as students move through schooling.
In this module, in the context of statistical data investigations, we build on the content of Year 5 on measurement data and count data with many different observed values of counts. Because these data types are quantitative, investigation and interpretation include considerations of representations and summaries of size and variation in size of observations.
In previous years, we have considered different types of data. When we collect or observe data, the ‘what’ we are going to observe is called a statistical variable.
You can think of a statistical variable as a description of an entity that is being observed
or is going to be observed. Hence when we consider types of data, we are also considering types of variables.
Some examples of measurement data are:
All measurement data need units of measurement and observations are recorded in the desired units of measurement.
Measurement data have units of measurement and are recorded with a certain precision that depends on the measuring instrument, the choice of the investigator and practical restrictions. Measurement variables are examples of continuous variables; continuous variables can take any values in intervals. For example, if someone says their height is 149 cm, they mean their height lies between 148.5 cm and 149.5 cm. If they say their height is 148.5 cm, they mean their height is in between 148.45 cm and 148.55 cm. If someone reports their age as 12 years, they (usually) mean their age is in between 12 and 13 years. Note the convention with age is that the interval is from our age in whole number of years up to the next whole number of years. If someone says their age is 12 and a half, is there a standard way of interpreting the interval they are referring to? Do they mean 12.5 years up to 13 years, or do they mean some interval around 12.5 with the actual interval not completely specified? Notice that our specification of intervals in talking about age is usually not as definite as when we quote someone’s height, but the principle is the same − observations of continuous variables are never exact and correspond to little intervals.
A count variable counts the number of items or people in a specified time or place or occasion or group. Each observation in a set of count data is a count value. Count data occur in considering situations such as:
We can see that the first example above of a count variable contrasts with the other examples, in which counts will tend to take many different values − that is, in data on the variables in bullet points 2, 3 and 4 above, repetitions of values of observations are not likely. Also, the sizes of the observations will tend to be large, sometimes very large. For these types of count variables, the types of graphs and summaries used for continuous variables are often appropriate.
This module uses a number of examples of continuous data or count data with many values to introduce one of the graphs that group values into intervals (the stem and leaf plot) and some quantities that are calculated from data and that represent certain features of data. Such quantities are called summary statistics. The examples and new content are developed within the statistical data investigation process through the following:
Such phases lend themselves to representation on a diagram, as follows.
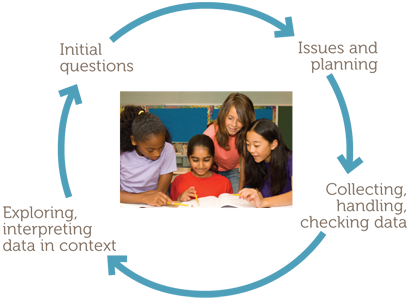
The examples consider simple situations familiar and accessible to Year 7 students
and in reports in digital media and elsewhere, and build on the situations considered in F- 5. The module also includes tips on possibly misleading aspects of summaries of continuous data.
Initial questions that can motivate an investigation
The following are some examples that involve collecting, or accessing, or finding,
and investigating data for at least one continuous or large count variable.
The above are examples of just some of the many questions or topics that can arise that involve data on at least one continuous variable or count data with many different values. Some of these examples are used here to explore the progression of development of learning about data investigation and interpretation. The focus in this module in exploring, representing and interpreting is on continuous variables or count variables that can take many different − usually large − values, but on one variable at a time.
General statistical note for teachers
A continuous variable takes values along a continuum. You can think of a continuous variable as one that is recorded or observed 'rounded off' to a number of significant figures that may depend on the recording or measuring device, or on convenience, or on the context, or on practical considerations. It is easy to see that measurement data are continuous because one of the key aspects of using a measuring device is its accuracy. So lengths, weights, time are measured 'to the nearest ….'.
In contrast, although it is easy to give ages to greater accuracy than in units of years − for example, months or even days − we tend to use units of days, weeks and then months only for babies and then toddlers. We might use quarter and half for children and even adults (for example, 'he’s nine and a half') but this usually refers to a vaguely-defined interval. For older children and adults, we tend to just use units of years for ages, and for greater accuracy tend to give the month or even date of birth. For example, 'I’m 15; my birthday is in May'. A mistake sometimes made by students when they first consider age from a statistical variable point of view is to say that it is a count variable 'because we count the years'. Although none of the examples discussed in this module involve age, it may arise in the course of discussion or investigations by students.
In some situations or investigations, it may happen that only a few ages in years are observed or recorded, and in this case, in more advanced modules, it might be treated as a variable that separates subjects into groups − that is, used as a categorical variable even though its essential nature is measurement. In some investigations, for example in some surveys, instead of recording age, only age groups are used, with subjects classified into one of a number of age groups. Almost always such age groups are not of equal length, so the variable 'age group' is a categorical variable that has been formed from the underlying continuous variable.
Another variable that can cause confusion is amount of money. Although the units of money are physical entities that can be held, amount of money is essentially continuous. This is easily seen when one considers how hourly wages are quoted as well as quantities such as exchange rates, share prices. Again, none of the examples discussed in this module involve amounts of money, but it is a variable that may arise in investigations designed by students of this year and older.
Identifying issues and planning
In the first part of the data investigative process, one or more questions or issues begin the process of identifying the topic to be investigated. In thinking about how to investigate these, other questions and ideas can tend to arise. Refining and sorting these questions and ideas along with considering how we are going to obtain data that is needed to investigate them, help our planning to take shape. A data investigation is planned through the interaction of the questions:
Planning a data investigation involves identifying its variables, its subjects (that is, on what or who are our observations going to be collected) and how to collect or access relevant and representative data.
Example A: reaction times
There are many ways of defining and measuring reaction times. One simple way is for one person to hold a ruler a certain distance (selected by the experimenter) vertically above a subject’s hand. When the ruler is dropped the subject must catch it. The distance up the ruler to the subject’s hand (provided the ruler is caught!) is a measure of reaction time. Note that a distance measurement here is being used as a measure of time − reaction time.
There are games available for computers or on the web that could be used to measure reaction time; different formats measure different types of reaction times and may also involve other capabilities or types of reactions.
One fun one that includes keyboard or mouse speed, is Go for the Gopher, which you can find under Games, on the Conker statistics website, http://conkerstatistics.co.uk/ . A gopher pops out of holes numbered 1 to 9, and the player tries to whack the gopher back into the hole, using either the mouse to work the mallet or the numbers on the computer keyboard. The program records the time from the gopher appearing out of a hole to the player whacking the gopher. In each game, the gopher pops up 10 times from randomly chosen holes. Hence each game has 10 reaction times recorded. This is a rather small set of data. More data could be collected for one player by repeating the game − aspects of this are considered in the next section. The variable is reaction time, and observations are taken for each 'pop up' of the gopher.
Another possibility is to collect the best (that is, the smallest) reaction time for each game played by different students. The variable then is best time out of 10, and the data are observed on different players.
Example B: estimating a length of time
How well do people estimate a length of time such as 10 seconds or a minute? And how should they be asked to estimate it? One way is to use a stopwatch and start the stopwatch and the subject on 'go' with the subject calling 'stop' when they think the time period is finished. Their estimate is the time recorded by the stopwatch. The variable is the guessed or estimated time and the observations are recorded per person.
Example C: measurements of fish
Recording weight and length of fish caught is fairly straightforward, except for ensuring that length is measured consistently. In practice, the species of fish and the location of the catch would also be recorded, as weights and lengths by themselves do not provide all the information.
Example D: optical illusions
As in Example C, there are likely to be a number of variables of interest in this type of investigation. In this example in the Year 6 module, the two variables of interest were which picture is seen first and the gender of the person looking at the picture(s). In this module we focus on the variable length of time (in seconds) until the picture is seen, regardless of which picture is seen first.
Data for this investigation is straightforward and quick to collect to obtain many observations and can be collected from fellow students and from family and friends. A brief explanation should be given to each subject. To record the time to see a picture, the explanation needs to be given before the picture is shown. Hence the explanation could be something like 'I’m going to show you a picture that could be seen as a picture of an old man or of a young man. Tell me as soon as you’ve seen either the old or young man, and which one you see.'
Example E: How often do people blink?
A time period needs to be chosen that is sufficiently long to represent a typical 'snapshot' of the subject’s blinking, but not too long for the observer to lose count. A minute could be a practical choice. To count the number of times someone blinks requires close observation which almost certainly affects the behaviour of the subject. A way of avoiding this problem and of creating conditions as similar as possible across subjects, is to work in pairs, with one person talking to, or 'interviewing', the subject while the other person unobtrusively counts the number of blinks. In this module, we just consider the number of blinks per minute of such an experiment, but in practice, as with other examples above, a number of variables are likely to be of interest, such as gender and age of the subject and of the interviewer, as it is likely that the combinations of these could affect the number of blinks.
Example F: ABS survey on Children’s Participation in Cultural and Leisure Activities Survey
This survey (available on the ABS website with the 2009 report being publication 4901.0) is an extensive survey covering a wide range of activities. Many variables are considered. As with many public reports, various types of summaries are available but not necessarily the raw data. As with all quality reporting, the ABS always includes in their reports clear and detailed information as to how the data were collected, and what it consists of. Two of the activities covered in the survey are bike riding and reading for pleasure. The survey asks for the number of times an activity is engaged in (usually over a year) and the amount of time spent on the activity during the most recent two weeks. The report considers age groups and gender. In this module, we focus on the duration of the activity in the most recent two weeks (for each respondent) for bike riding and for reading for pleasure. These are both in minutes and are continuous variables. We see the types of information that are typically given or not given in public reports of this nature.
General statistical notes for teachers’ background information
All of the above examples illustrate a challenge that is typical of collecting, recording or observing continuous data, namely, the care that is required in identifying or preparing the circumstances of the collection in order to obtain consistent conditions. Generally speaking, continuous data is rich in information but tends to require thought and effort in its collection.
Collecting, handling and checking data
As in Years 4, 5 and 6, the examples below identify possible practical challenges in addition to any mentioned above, and include illustrations of the first few rows of suggested recording sheets. The following note is very helpful in planning and preparation for collecting data.
General statistical note
Note in the examples in previous years, and in the examples below in which data are collected (rather than obtained from a secondary source) how the subjects and variables of a statistical data investigation can always be represented by a recording sheet or spreadsheet with rows and columns, where each subject has a row and each variable has a column, and the column names identify the variables. That is, each time we collect or take an observation, we enter data in one of the rows, corresponding to one subject. If we are collecting or observing three observations per subject, we have three bits of data to enter, one in each column. For example, if we are doing the optical illusions investigation, and recording gender, picture first seen and time to see the picture, we would have 3 observations for each subject and hence 3 columns. We might include another column in the recording sheet with the subject’s name (or in general, some identifier) so that we can check the data if necessary or to avoid duplicates. A more extensive investigation might include other variables such as age and some characteristic that might be of research interest, such as dominant hand.
In this module, we focus only on the continuous variables of an investigation, and only on one at a time. Focus on a combination of a continuous and a categorical variable, or on combinations of continuous variables occurs in more advanced modules.
Example A: reaction times
If a game such as Go for the Gopher is used, and reaction times for each 'pop up' of the gopher recorded for a single player, consideration needs to be given to whether to have a trial run or not. If the game has a fixed number of 'pop ups' such as 10, and more observations are desired, the game must be repeated, in which case a trial game before observations are recorded is advisable. If data are collected for one player, the recording sheet is simple, although it may be advisable to record the game number and to retain the order within the game, in case any unusual features emerge. For the Go for the Gopher game, the reaction times are automatically recorded for each game and can be downloaded. The first few lines of a recording sheet would look like the following.
| Game | Observation number | Time in seconds |
| 1 | 1 | 1.09 |
| 1 | 2 | 1.1 |
| 1 | 3 | 1.04 |
If it is decided to investigate performance across a number of subjects, for example, all the students in a class, either the best (that is, smallest) reaction time could be used per student or the total reaction time per student (that is, the sum of each student’s reaction times in a game). One advantage of the total reaction time would be to make some allowance for the variation in which holes the gopher appears within a game. The first few lines of a recording sheet for this approach would look like the following.
| Student | Total reaction time in seconds |
| 1 | 10.5 |
| 2 | 9.55 |
| 3 | 11.5 |
Example B: estimating a length of time
A trial might be useful for choosing the period of time to be estimated, to ensure that there are no practical problems and to facilitate consistency of conditions for different students collecting data. Discussion on who to ask − that is, the subjects of the investigation − and circumstances under which they can be asked, is also advisable to obtain consistency of conditions. For example, is there to be any restriction on age groups? Should care be taken so that subjects are not under pressure, for example, focussing on another activity or in a hurry? Students might choose to record gender and age group even though the focus will just be on the continuous variable, in case any anomalies in the data may be explained by other considerations. If subjects are asked to estimate 10 seconds, and if gender but not age group is recorded, the first few rows of a recording sheet would look like the following. The recording of the name of collector and subject is for data checking purposes, or for reference for discussion in the case of any unusual observations showing up in the data.
| Subject name | Gender | Collector name | Estimate of 10 seconds |
| Mrs Brown | F | Andrew | 9.5 |
| Abigail Brown | F | Andrew | 10.2 |
| Mr Jones | M | Alice | 8.9 |
Note that the variables are gender (categorical) and estimate of 10 seconds (continuous).
Example C: Fish measurements
Data on fish might not be possible to collect unless students have relatives and/or friends who are keen fishers. Data might be available from government departments, either fishery or environmental departments, or from environmental research or agencies. Whether data are available from recreational fishing or from research sources, the circumstances of the fishing are needed for discussion as it is important to know all relevant information for discussion. A recording sheet from a fishing trip at one location could look like the following, with a row for each fish.
| Angler | Species | Weight in gms | Length in mm |
| 1 | Bream | 395 | 250 |
| 2 | Bream | 720 | 360 |
| 2 | Dart | 370 | 240 |
Example D: Optical illusions
As described above, data for this investigation is straightforward and quick to collect to obtain many observations and can be collected from fellow students and from family and friends. To record the time to see a picture, the explanation needs to be given before the picture is shown. Hence the explanation could be something like 'I’m going to show you a picture that could be seen as a picture of an old man or of a young man. Tell me as soon as you’ve seen either the old or young man, and which one you see.' Because circumstances for recording time to see a picture need to be consistent across data collectors, some trials amongst collectors would be of assistance. Although the interest in this module is on the time to see a picture, no matter which picture, it is likely that students would be interested in recording which picture is seen first and the gender of the subject. If this investigation has not been done before, the students might be interested in investigating the pair of categorical variables (gender and picture seen) as revision of Year 6 content as well as exploring the continuous variable (time to see the picture). The first few rows of the raw recording sheet would look like:
| Student name | Gender |
Picture seen first |
Time to see picture in seconds |
| Frances | G | Y | 1.34 |
| Stefan | B | Y | 1.50 |
| Alisha | G | O | 3.12 |
Example E: How often do people blink?
Decisions for collecting these data include length of time (a minute is an appropriate length) and the conditions under which the blinks are going to be counted. The subjects should not know their blinks are being counted, and the conditions need to stay as consistent as possible. Students should work in pairs to collect these data, and if an 'interview' is going to be the conditions under which the data are collected, the same questions should be asked of each subject. Students collecting the data should ensure they are using the same conditions; some role play in the planning could be fun as well as useful in preparation. Identifiers for the collectors should be used and possibly for the subjects in case anomalies or interesting features of the data show up and the circumstances need to be checked. The first few rows of the raw data sheet could look something like the following.
| Student pair | Subject | Number of blinks per minute |
| Frances/Stefan | Mrs Smith | 14 |
| Frances/Stefan | Bradley | 2 |
| Frances/Stefan | Mr Jones | 13 |
Example F: ABS survey on Children’s Participation in Cultural and Leisure Activities Survey
The following is an extract from the ABS report 49010 on the issue of time children spend reading for pleasure.
| Australian Bureau of Statistics | ||||
| 49010 Apr 2006 Children’s Participation in Cultural and Leisure Activities, Australia | ||||
| CHILDREN WHO READ FOR PLEASURE, Duration in last two weeks | ||||
| AGE GROUP (YEARS) | ||||
| 5−8 | 9−11 | 12−14 | Total | |
| NUMBER(‘000) | ||||
| 2 hours or less | 206.9 | 134.8 | 112.3 | 453.9 |
| 3−4 hours | 150.1 | 103.8 | 106.1 | 360.0 |
| 5−9 hours | 268.2 | 207.2 | 160.6 | 636.0 |
| 10−19 hours | 125.9 | 142.0 | 153.0 | 420.9 |
| 20 hours or more | 20.4 | 37.2 | 55.7 | 113.3 |
| Total | 771.5 | 624.9 | 587.7 | 1984.0 |
Note that the data on the continuous variable, time spent reading, are grouped. Whether the question was asked with these categories, or whether the grouping was done after the data were collected would need further investigation of the report. It is possible that this information may not be easily found in the report. Public reports do not necessarily contain all of the detailed information about the collection of the data.
Note also that the groupings are not of equal lengths of time, so the continuous variable, time spent reading, has been turned into a categorical variable in this table.
The table giving time spent bike riding is similar in that only groupings of observations are given. The same groupings of times are used as for duration of reading for pleasure.
Exploring and interpreting quantitative data:
dotplot and stem-and-leaf plot
In Year 5, dotplots were used for plotting measurement data and count data where appropriate (usually for count data with a reasonable number of different values and/or when we want to keep the values of larger counts). A dotplot plots quantitative data, with a dot on the graph for each value in the set of quantitative data. If a value occurs 3 times, there are 3 dots in a line above that value. Hence the heights of the columns of dots give the frequencies of the data values. If there are many observations in the dataset, each dot might represent two observations. For quantitative data, a dotplot is a plot of the 'raw' data with no grouping of values. So if a set of quantitative values is not large and has many different values, a dotplot is not very informative, but a dotplot is usually an excellent way to have a first look at data. Dotplots are easily done by hand and are also available in most statistical software.
Example A: reaction times
Below is a dotplot of 20 reaction times for one person in the Go for the Gopher game. These have been collected from two 'games' of 10 'pop-ups' of the gopher in each.

We see that the reaction times for this person had a range from 0.84 secs to 1.34 secs. All but two lie from 0.84 secs to 1.12 secs. For interest, only one of these was an initial time in a group of 10 tries.
General statistical note
The word range is used in statistics in the same way as everyday speech as a verb, e.g. 'the values of the observations range from 0.84 secs to 1.34 secs'. But as a noun it is used to give the distance between the smallest and the largest observations. In this example, the range of the data is 1.34-0.84 = 0.5 secs. The range of the data gives a summary of how spread out the observations are. Another person’s reaction times might range from 0.5 secs to 1.45 secs, so the range of the data for that person is 0.9 secs. Their best time is smaller but their variability is greater.
Example B: estimating a length of time
Below is a doptplot of estimates of 10 seconds by randomly chosen people asked (separately − that is, none of the subjects were present when another subject estimated 10 seconds) to guess when 10 seconds was up from being told 'go'.
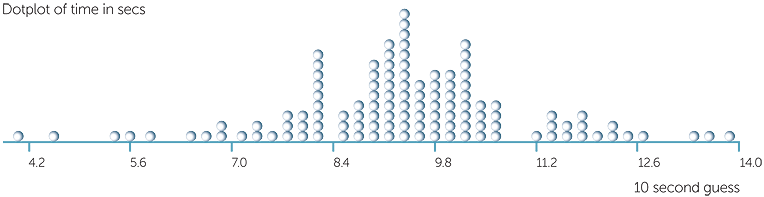
We see that the guesses range from approximately 4.1 seconds to just under 14 seconds, with a range of the data of approximately 13.9-4.1 = 9.8 secs. Most of the observations are under 10 secs.
In Examples A and B above, we see that although dotplots are good plots of raw quantitative data for a first 'look' at the data, there are some limitations to them. They are 'bumpy' and the exact values of the observations are not necessarily available. They are 'bumpy' because continuous data can take any values in intervals, so the occurrence of particular values in a dataset is due to a combination of chance and precision of observation. That is, the 'bumpiness' of continuous data is like unevenness in a path or a road, and, just like small unevennesses in a path or road, these can distract from the overall features or behaviour of the data.
Continuous data are often presented in terms of intervals of values. This not only smooths the 'bumps' but is also a better representation of the nature of continuous variables because they take values in intervals. For example, if a stopwatch is used in collecting data on people’s guesses of 10 seconds, and the stopwatch records times to the nearest 10th of a second, then a guess recorded as being 9.6 secs is a guess between 9.55 and 9.65 secs.
One plot for quantitative data that smooths the 'bumpiness' and has an added advantage of retaining the original values of the data (correct to a certain number of figures which depend on the range of the data) is the stem-and-leaf plot.
Below is a stem-and-leaf plot for the data of Example A. The plot consists of a stem which is the first column below and leaves which are in the second column. The leaf unit is 0.01 secs, so the digits in the leaves are the digits in the second decimal place. This means that the numbers in the stem are in 10ths of seconds. Each observation is recorded by an entry in a leaf, and if there is more than one observation with the same value to the nearest 100th of a second (in this plot) then the digit representing this value is repeated. In the plot below, we see that there is one observation of 0.84secs, one of 0.85secs, one of 0.87secs, two of 0.89secs, ….., three of 1.03 secs, etc.
In the plot below, the intervals being used for the leaves are of length 0.05 secs, so that, for example, values of 1.00 up to 1.04 (correct to two decimal places) are in one leaf, and values from 1.05 to 1.09 are in the next leaf. If there are no entries in a leaf, there are no observations with values in that interval. In the plot below, there are no observations in the intervals 1.15 to 1.19 or 1.20 to 1.24. Because there are only 20 observations in this dataset, the stem-and-leaf plot still has some 'bumps' but it is reasonably clear that there are two large observations that are bigger than the rest, and that the other observations tend to fall into two groups, one from 0.84 to 0.93 and the other from 0.96 to 1.02. It would be interesting to see if other players’ reaction times also tended to fall into groups and to discuss why this might be.
Stem-and-leaf plot of reaction time in secs in Example A
Leaf unit is 0.01 secs
| 8 | 4 | |
| 8 | 5799 | |
| 9 | 22223 | |
| 9 | 6 | |
| 10 | 3334 | |
| 10 | 9 | |
| 11 | 02 | |
| 11 | ||
| 12 | ||
| 12 | 8 | |
| 13 | 4 |
Example B: estimating a length of time
Below is a stem-and-leaf of the estimates of 10 seconds of Example B. There were 120 subjects who were asked to guess 10 seconds. The leaf unit is 0.1 second, so the digits in the leaves are the 10ths of seconds. Hence the digits in the stem are in the units places. The range of the data has been divided into intervals each of 1 second in length, so that, for example, the leaf corresponding to the stem of 9 has all the observations with values ranging from 9.0 up to 9.9 secs.
There is one observation of 3.9 secs, two observations of 6.7 secs, five observations of 8.1 secs, etc.
We see that the stem-and-leaf plot gives us a smoother picture of the data and retains the values of the observations to reasonable accuracy. We see that most of the subjects gave between 8 secs and 10.6 secs as their guess for 10 secs. If we want to find the frequencies or relative frequencies of any intervals of interest, it is easy to add up the numbers of observations in any interval. For example, 16 out of 120 subjects gave their guesses as less than 8 secs, while 8 out of 120 people gave guesses at 12 secs or more.
Stem-and-leaf plot of guesses of 10 secs
Leaf unit is 0.1 second
| 3 | 9 | |
| 4 | 5 | |
| 5 | 469 | |
| 6 | 3577 | |
| 7 | 1346778 | |
| 8 | 000111112222666888899999 | |
| 9 | 00011111112223333333344444555666778888899 | |
| 10 | 0000011111222223344566 | |
| 11 | 133456777 | |
| 12 | 02246 | |
| 13 | 248 |
Example C: Fish measurements
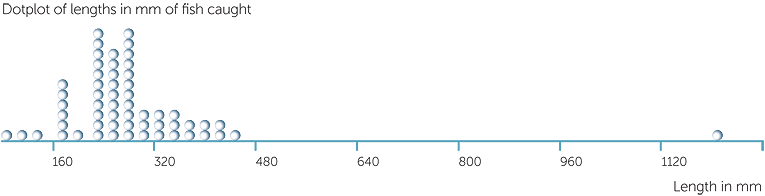
Below are a dotplot and a stem-and-leaf plot of the lengths in mm of fish caught on a weekend fishing trip on Stradbroke Island in Queensland. We see that there is one very very long fish; checking the original recording sheets which also listed the species, shows that this is a reef shark. Yes, a shark is a fish but it is very different from other fish and including this observation is making it difficult to see what the rest of the data look like. So a stem-and-leaf plot without the shark is also given.
Stem-and-leaf of lengths in mm of fish caught
Leaf unit = 10mm
| 0 | 89 | |
| 1 | 1778888 | |
| 2 | 0333344444445555555567777778888899 | |
| 3 | 011234456789 | |
| 4 | 01 | |
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | 0 |
Stem-and-leaf of lengths in mm of fish caught without the shark
Leaf unit = 10mm
| 0 | 89 | |
| 1 | 1 | |
| 1 | ||
| 1 | ||
| 1 | 77 | |
| 1 | 8888 | |
| 2 | 0 | |
| 2 | 3333 | |
| 2 | 444444455555555 | |
| 2 | 6777777 | |
| 2 | 8888899 | |
| 3 | 011 | |
| 3 | 23 | |
| 3 | 445 | |
| 3 | 67 | |
| 3 | 89 | |
| 4 | 01 |
Without the shark we can see that the lengths of the fish caught ranged from 80 mm (correct to nearest mm) to 410 mm, so a range of data of 330 mm. There seem to be groups of lengths; it is possible that these relate to different groups of species of fish.
Example D: optical illusions
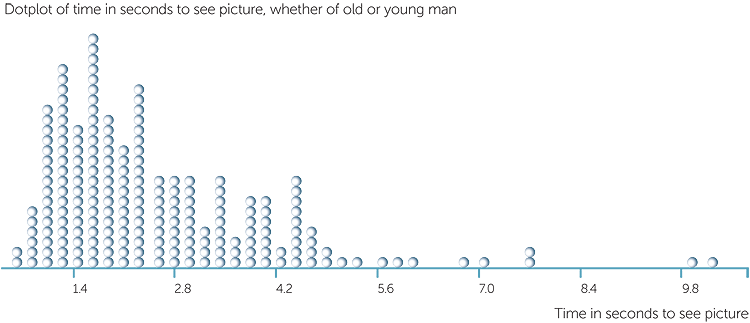
203 students were shown the optical illusion picture and asked whether they could see an old or a young man. Below are a dotplot and a stem-and-leaf plot of the time in seconds taken to see a picture no matter what the picture was. We see that the minimum time was 0.5 sec and the maximum time was 10.4 secs, and that most people took somewhere between 0.5 sec and 4.5 secs, but that a small number (9 people) took more than 5.5 seconds. The stem-and-leaf plot has smoothed the unevennesses of the dotplot which helps to see the pattern of the data. It has grouped the data into intervals of length = 1 sec because the people who took longer than 5 secs are very spread out. This has produced a stem-and-leaf plot with one group (those who took at least 1 but less than 2 secs to see a picture) with so many observations that they are not all represented on the plot. Once the leaf has become too large for the restrictions of the page, a + sign tells us that there are more observations in this group but not how many.
Stem-and-leaf of time in seconds to see picture, whether of old or young man
Leaf unit = 0.1
| 0 | 56778888999999 | |
| 1 | 00000000001111111111112222222233333333444444555555555566666666666+ | |
| 2 | 000111111112222222222333333444555555566778899999 | |
| 3 | 0000112333344455555557899 | |
| 4 | 000000022223457 | |
| 5 | 68 | |
| 6 | 059 | |
| 7 | 55 | |
| 8 | ||
| 9 | ||
| 10 | 04 |
We could choose to do a stem-and-leaf plot with half-second intervals although this would give us a rather large plot.
General statistical notes
Note that it is important to ensure that intervals of equal size are used in a stem-and-leaf plot, just as it is important not to omit intervals along the x-axis of a dotplot. This is because we are dealing with quantitative data and need to see how the data are spread over the possible quantitative values, and how big are the distances between any groups of data. Indeed, if we don’t have intervals of equal size in a stem-and-leaf plot, we would turn continuous data into categorical data! And lose the important information associated with quantitative data.
Example E: How often do people blink?
Below are a dotplot and a stem-and-leaf plot of the number of blinks in a minute for 101 subjects who were interviewed by pairs of data collectors, using the same questions, with one of the pair asking the questions and the other, standing slightly to the side, unobtrusively counting the number of blinks.
We see that the number of blinks per minute under interviewing circumstances ranged from 2 to 53 − a range of 51! Notice that the stem-and-leaf is smoother than the dotplot, but at the cost of obscuring the considerable variation in these data. We could divide up the intervals more in the stem-and-leaf, but we would have to increase the number of intervals to 26. Why? Because we need to divide into equal size intervals with integer stem values, so the choice here is intervals containing 10 different values, 5 different values (as here) or 2 different values.
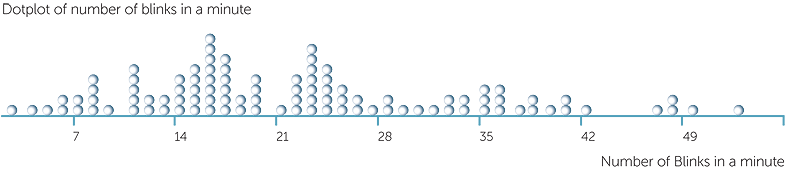
Stem-and-leaf plot of number of blinks in a minute
Leaf unit = 1.0
| 0 | 24 | |
| 0 | 5667788889 | |
| 1 | 1111122334444 | |
| 1 | 5555566666666777777889999 | |
| 2 | 12222333333344444 | |
| 2 | 555667889 | |
| 3 | 012233444 | |
| 3 | 5557889 | |
| 4 | 0024 | |
| 4 | 788 | |
| 5 | 03 |
Note that the number of blinks is a count variable but because the range of the data is 51, it behaves like a continuous variable, and the plots for continuous data are appropriate.
Example F: ABS survey on Children’s Participation in Cultural and Leisure Activities Survey
It is not possible to draw a dotplot or a stem-and-leaf plot of the data in Example F because we do not have the raw data, and the intervals given in the table do not have equal distances. And all we know about the range of the data is that it is at least 2 to 20 hours in a fortnight, but the implication of the table is that it ranges at least some way less than 2 hours and greater than 20 hours.
Exploring and interpreting quantitative data:
mean and median
In each of the above examples, the minimum, maximum and range of the data gives us some idea of the types of values, and, in particular, the spread of values. However it would be of benefit to be able to quote some quantity that in some way represents the general size of the variable. Two such quantities are the average or mean of the data, and the median of the data.
The average or mean of the data is obtained by adding all the values of the observations and dividing by the number of observations.
The median of the data is the middle value − the value that has half the observations less than it in value, and half the observations greater than it in value.
If the number of observations is an odd number, then the median of the data is one of the values observed − the middle value with equal numbers of observation less than it and greater than it. If the number of observations is an even number, then the median of the data is taken as halfway between the two middle values so that again there are equal numbers of observations less than and greater than it.
The average and the median are calculated below for each of the Examples above,
with comments on how they compare and how well they represent the general size of the observations.
Example A: reaction times
The average or mean of the 20 reaction times of Example A, is calculated by (0.84 + 0.85 + 0.87 + 0.89 + 0.89 + …. + 1.34)/20 = 0.9985 secs (= 1 sec to nearest 10th of a second)
The median of the 20 reaction times is halfway between the 10th and the 11th observations when they are arranged from smallest to largest. Because the stem-and-leaf plot has arranged the observations from smallest to largest, it is very easy to use the stem-and-leaf plot to obtain the median. In the stem-and-leaf plot, the 10th observation from the smallest is 0.93 sec and the 11th is 0.96 sec, so halfway between these two is 0.945 sec.
The median is slightly smaller than the mean because the two largest values are added to the rest to get the total to be divided by 20, whereas for the median, it only matters that they are the two largest values. That is, if the two largest values were 1.18 and 1.24 instead of 1.28 and 1.34, the mean of the data would be smaller but the median of the data would not change. However if the value of 1.34 was removed from the data, the mean and the median would both change. They would both decrease but the mean would decrease most. The mean would become 0.9805 secs. The median would simply be the 10th observation, which is 0.93 secs.
Example B: estimating a length of time
The average or mean of the 120 guess times of Example B, is calculated by
(3.9 + 4.5 + 5.4 + …. + 13.4 + 13.8)/120 = 9.4 secs. [Aside: 9.4 is calculated from the original data which has two decimal places; the average calculated using just the stem-and-leaf values may be slightly less than this.]
The median of the 120 guesses is halfway between the 60th and the 61st observations when they are arranged from smallest to largest. Because the stem-and-leaf plot has arranged the observations from smallest to largest, it is easy to use the stem-and-leaf plot to obtain the median. In the stem-and-leaf plot, the 60th observation from the smallest is 9.3 sec and the 61st is also 9.3 sec, so halfway between these two is 9.3 sec.
Hence the average or mean of the data and the median of the data are the same (allowing for rounding).
Example C: Fish measurements
The average or mean of the 58 lengths of fish of Example C, is 277.76 mm calculated from the stem-and-leaf plot. It is obtained by (80 + 90 + 110 + 170 × 2 + … + 410 + 1200)/58. It is 278.8 mm when calculated from the original data.
The median of the 58 lengths is halfway between the 29th and the 30th observations when they are arranged from smallest to largest, because this gives 29 observations less than and greater than it. Because the stem-and-leaf plot has arranged the observations from smallest to largest, it is easy to use the stem-and-leaf plot to obtain the median. In the stem-and-leaf plot, the 29th observation from the smallest is 250 mm and the 30th is 260 mm, so halfway between these two is 255 mm.
Thus the average of the data is considerably greater than the median of the data. This is because of the very large observation of 1200 mm, which is the shark. Although the shark is a fish, there are good reasons for omitting this observation from the data if we are wishing to focus on fish species other than sharks. If this observation is omitted, the average length of the 57 observations calculated from the stem-and-leaf plot is 261.58 mm (262.67 mm using the original data) and the median is the 29th observation which is 250 mm.
Notice that if the observation of 1200 mm was 500 mm, the median would still be 255mm while the average would be 265.7mm. The average is affected by the actual values of the smallest and largest observations, while the median is affected by their presence or absence.
General statistical notes
The value of the median of data is realised in more and more situations because of its ease of interpretation − half the observations are less than (or equal to) it, and half are greater than (or equal to) it. Examples where medians are often quoted now include house prices in different districts, incomes, etc.
Example D: optical illusions
The average or mean of the data for 202 subjects on how long they took to see a picture was 2.366 secs (obtained from the original data). The median is halfway between the 101st and the 102nd observation after they are arranged from smallest to largest, so that it has 101 observations on each side of it. The stem-and-leaf plot above cannot be used to find the median because of the very large number of observations between 1 and 2 secs. A stem-and-leaf plot with more groups is given below. Also given is a column that adds up the numbers of observations from the smallest and the largest, to make it easier in using the plot to obtain the median and other features seen in later years.
Stem-and-leaf of time in seconds to see picture, whether of old or young man
Leaf unit = 0.1 sec
| 14 |
| 58 |
| (47) |
| 97 |
| 67 |
| 49 |
| 35 |
| 24 |
| 11 |
| 9 |
| 9 |
| 7 |
| 6 |
| 4 |
| 4 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 0 |
| 1 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| 5 |
| 6 |
| 6 |
| 7 |
| 7 |
| 8 |
| 8 |
| 9 |
| 9 |
| 10 |
| 56778888999999 |
| 00000000001111111111112222222233333333444444 |
| 55555555556666666666666777777888888888999999999 |
| 000111111112222222222333333444 |
| 555555566778899999 |
| 00001123333444 |
| 55555557899 |
| 0000000222234 |
| 57 |
| 68 |
| 0 |
| 59 |
| 55 |
| 04 |
There are 14 observations in the first group of the smallest times, and 44 in the next group which is added to 14 to give 58 in the first two groups. The group that contains the median is the next group; it has 47 observations in it, so added to 58, this would take us past the median. From it, we see that the 101st observation is 1.9 and the 102nd is 1.9, so that the median of these data is 1.9 secs based on this stem-and-leaf plot.
Notice that again we have a situation in which the average or mean is larger than the median because almost all of the times are less than 4.5 secs, but a relatively small number of people took longer.
Example E: How often do people blink?
The average or mean number of blinks of 101 people who were interviewed as described above was 22.25. Even though number of blinks is a count variable and must therefore take whole numbers, we leave the average as 22.25 because it is representing the dataset not an individual person. The median is the 51st observation when they are arranged from smallest to largest, so that it has 50 observations on each side of it. The stem-and-leaf plot is given again below with the extra column for recording the totals of the numbers of observations as we move from the outsides (the smallest and the largest) towards the 'middle'. We see that the 51st observation and hence the median is 21 blinks in a minute. Note that the observations 'clump' together more for the smaller values than the larger values, and hence the average is slightly greater than the median, but the contrast is less than in other examples because there are not large observations that are separate from the rest of the data.
Stem-and-leaf plot of number of blinks in a minute
Leaf unit = 1.0
| 2 |
| 12 |
| 25 |
| 50 |
| (17) |
| 34 |
| 25 |
| 16 |
| 9 |
| 5 |
| 2 |
| 0 |
| 0 |
| 1 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| 24 |
| 5667788889 |
| 1111122334444 |
| 5555566666666777777889999 |
| 12222333333344444 |
| 555667889 |
| 012233444 |
| 5557889 |
| 0024 |
| 788 |
| 03 |
Example F: ABS survey on Children’s Participation in Cultural and Leisure Activities Survey
The report from the ABS (report 49010 on http://www.abs.gov.au/) on the time children spend on various activities in a fortnight provides averages and medians. For children who read for pleasure, the report gives an average and a median amount of time in hours in a fortnight for different age groups. For the 12-14 year age group, the average is quoted as 8.5 hours and the median as 6 hours. For those who participate in bike riding, for the 12-14 age group, the average time in the preceding fortnight to the survey is given as 5.9 hours and the median as 4 hours.
From the examples above, we can surmise that there are a small number of children who read a lot and also a small number who ride a bike a lot. Indeed, the report also includes the information that 9.5% of 12-14 year olds who read for pleasure read more than 20 hours a fortnight, and that 6.2% of 12-14 year olds who participate in bike riding, ride more than 20 hours a fortnight.
A general statistical note for teachers’ background information
The average and median of data are often called measures of centre or measures of location because they provide information on the general size of the observations (hence location) and some idea of where the 'middle' of the data are (hence measures of centre). Unfortunately, the incorrect mention of 'mode' is often seen in association with mean and median. The concept of mode should not be introduced pre-calculus as it refers to local maxima of the mathematical model for a continuous variable, namely the probability density function. 'Modes' of data are often described as most frequently occurring values. For a categorical variable it makes sense to talk of the most frequently occurring category. But we can see in the dotplots of these examples, that the concept of most frequently occurring value in a set of continuous data is not only difficult to identify but also provides very little information.
In the stem-and-leaf plots, the unevennesses of the raw data have been smoothed out by grouping the observations into intervals, and in all the examples above, there is a group that could be called the 'modal class'. However what it is depends on how the observations are grouped − unlike the average and the median (allowing for rounding) − and, moreover, there is no reason why a modal class should represent the middle of the data. There may not be just one modal class, no matter how the data are grouped. For example, in a dataset on characteristics such as strength of grip or height, with both males and females, the data usually show two groups. Even if there is only one modal class for a particular grouping of a dataset, the modal class could be the first one for certain types of data. For example, the length of phone calls typically has many very small values and many values spread over a wide range of values up to very large ones.
In summary: what is a mode is not necessarily clear; modes are not necessarily measures of centre; and the concept of mode for continuous variables should wait until concepts of probability density functions are introduced.
Some general comments and
links from F-6 and towards year 8
Although measurement data have been introduced and experienced in Year 5, this module marks a significant step forward in generalising measurement data to continuous data, and emphasizing the key property of continuous data, namely that continuous variables take intervals of values. This module introduces one of the plots for continuous data in which the data are grouped to smooth the unevennesses that are typical of continuous data, and which allow focus on the overall behaviour of the data. Grouping of continuous data involves choices of groupings − there is not just one picture of grouped continuous data. The module also demonstrates that count data with many different counts is appropriately presented using plots for continuous data.
This module also introduces for the first time, average (or mean) and median of quantitative data, and demonstrates, through examples, how they represent in some way, the middle or location of quantitative data. The examples also demonstrate how the average and median of data are affected by large observations, and when they tend to be close in value and when they tend to differ.
As in Years 4-6, the examples of this module again illustrate the extent of statistical thinking involved in the initial stages of an investigation in identifying the questions/issues and in planning and collecting the data. Although the focus is still on considering just the data as collected or given, the above examples also show that at least some indications of concepts of 'what do our data represent' and variation in data across samples, tend to arise naturally in everyday situations that are very familiar to students.
The question of representativeness of data is considered further in Year 8, along with greater emphasis on recognising, exploring and interpreting variation within data and across datasets. As in Years F-7, concepts are introduced, developed and demonstrated in contexts that continue the development of experiential learning of the statistical data investigation process.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()
