The Improving Mathematics Education in Schools (TIMES) Project
Data Investigation and interpretation 8
Statistics and Probability : Module 5![]() Year : 8
Year : 8
June 2011
It is assumed that in Years F-7, students have had many learning experiences involving choosing and identifying questions or issues from everyday life and familiar situations, planning statistical investigations and collecting or accessing data. It is assumed that students are now familiar with categorical, count and continuous data, have had learning experiences in recording, classifying and exploring individual datasets of each type, and have seen and used tables, picture graphs and column graphs for categorical data and count data with a small number of different counts treated as categories, and dotplots and stem-and-leaf plots for continuous and count data. It is assumed that students are familiar with the use of frequencies and relative frequencies of categories (for categorical data) or of counts (for count data) or of intervals of values (for continuous data). It is assumed that students have used and interpreted averages (or means) and medians of quantitative (that is, count or continuous) data. It is assumed that students have become familiar with the concepts of statistical variables and of subjects of a data investigation. It is assumed that the focus in exploration and comment on continuous and count data has been on each set of data by itself, but that in Year 6, students have become familiar with considering more than one set of categorical data on the same subjects. In doing so, they have understood that they were investigating data on pairs of categorical variables.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
A natural environment for learning statistical thinking is through experiencing the process of carrying out real statistical data investigations from first thoughts, through planning, collecting and exploring data, to reporting on its features. Statistical data investigations also provide ideal conditions for active learning, hands-on experience and problem-solving. No matter how it is described, the elements of the statistical data investigation process are accessible across all educational levels.
Real statistical data investigations involve a number of components: formulating a problem so that it can be tackled statistically; planning, collecting, organising and validating data; exploring and analysing data; and interpreting and presenting information from data in context. No matter how the statistical data investigative process is described, its elements provide a practical framework for demonstrating and learning statistical thinking, as well as experiential learning in which statistical concepts, techniques and tools can be gradually introduced, developed, applied and extended as students move through schooling.
In this module, in the context of statistical data investigations, we build on the content of Years F-7 to focus more closely on whether we can use data to comment on a more general situation or population. We can do this if our data are, or can be considered to have been, a random set of observations obtained in circumstances that are representative of the general situation or population. Because this is a mouthful, we will here call this the random representativeness of data. So in this module we consider more about how data are collected, how to obtain random representative data and of what we can take our data to be representative. We compare the nature of censuses, surveys and observational investigations. Datasets that are not census data are often called samples of data, so this module includes some introductory notions of sampling to obtain random representative data.
The general meaning of the word sample is a portion, piece, or segment that is representative of a whole. In statistics, a sample of data, or a data sample, is a set of observations such that more, sometimes infinitely more, observations could have been taken. We want our sample of data to be randomly representative of some general situation or population so that we can use the data to obtain information about the general situation or population. A particular dataset might be considered to be representative for some questions or issues, but not for others, and these considerations will also be explored.
For example, if we wanted information about people’s opinions on water recycling, in some locality, then the ideal way of obtaining a sample of opinions that can be used to comment on the whole locality, is by taking a randomly chosen set of people from all of those in the locality and asking their opinions. However, even with complete records and resources available, this has many difficulties as we will see in this module. How about surveying people in a shopping centre on weekend days in that locality? This might be considered reasonably representative of people in that locality with respect to opinions on water recycling, but if we wanted information on people’s preferred time for shopping, then such a method would clearly be highly non-representative of people in that locality.
But even if weekend shoppers in a shopping centre in the locality can be considered representative of that locality, we also need to choose people randomly because only a randomly chosen group of people are truly representative of everyone in the locality.
In this module we use the term representative data to mean a set of observations obtained randomly in circumstances that are representative of a more general situation or larger population with respect to the issues of interest.
We build on the notions of variation introduced across Years F-7 to explore this concept more closely, including sources of variation within and across datasets.
In Year 7, we have seen the concept, use and interpretation of the average of a set of quantitative data; the average is often called the sample mean. We have seen the concept, use and interpretation of relative frequency of a category for categorical data; this is often called the sample proportion (for that category). In this module, consideration of variation across datasets leads us to explore the variation of sample means and of sample proportions across datasets collected or obtained under the same or similar circumstances.
This module uses a number of examples involving the different types of data to explore representativeness of data, variation across and within datasets, and the variation of quantities calculated from data, such as averages or sample means, and sample proportions. Such quantities are called summary statistics. The examples and new content are developed within the statistical data investigation process through the following:
- considering initial questions that motivate an investigation;
- identifying issues and planning;
- collecting, handling and checking data;
- exploring and interpreting data in context.
Such phases lend themselves to representation on a diagram, as follows.
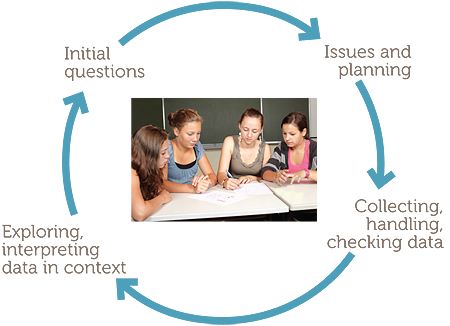
The examples consider situations familiar and accessible to Year 8 students and in reports in digital media and elsewhere, and build on the situations considered in F-7. The module uses concepts, graphs and other data summaries considered in F-7, but focuses on the planning and collecting components of the statistical data investigation process to develop understanding of concepts of representativeness, sources of variation, sampling and variation due to sampling.
Revision of types of data and statistical variables
In F-7, we have considered different types of data, and hence different types of statistical variables. When we collect or observe data, the ‘what’ we are going to observe is called a statistical variable. You can think of a statistical variable as a description of an entity that is being observed or is going to be observed. Hence when we consider types of data, we are also considering types of variables. There are three main types of statistical variables: continuous, count and categorical.
Some examples of continuous variables are:
- time in minutes to get to school
- length in cm of right feet of Year 7 girls
- age in years
- amount of weekly allowance
All continuous data need units and observations are recorded in the desired units.
Continuous variables can take any values in intervals. For example, if someone says their height is 149 cm, they mean their height lies between 148.5 cm and 149.5 cm. If they say their height is 148.5 cm, they mean their height is in between 148.45 cm and 148.55 cm. If someone reports their age as 12 years, they (usually) mean their age is in between 12 and 13 years. Note the convention with age is that the interval is from our age in whole number of years up to the next whole number of years. If someone says their age is 12 and a half, is there are a standard way of interpreting the interval they are referring to? Do they mean 12.5 years up to 13 years, or do they mean some interval around 12.5 with the actual interval not completely specified? Notice that our specification of intervals in talking about age is usually not as definite as when we quote someone’s height, but the principle is the same − observations of continuous variables are never exact and correspond to little intervals.
A count variable counts the number of items or people in a specified time or place or occasion or group. Each observation in a set of count data is a count value. Count data occur in considering situations such as:
- the number of children in a family
- the number of people arriving at a central city railway station in a 5 minute interval during peak time
- attendance at football matches
- the number of hits on an internet site per week
We can see that the first example above of a count variable contrasts with the other examples, in which counts will tend to take many different values − that is, in data on the variables in bullet points 2, 3 and 4 above, repetitions of values of observations are not likely. Also, the sizes of the observations will tend to be large, sometimes very large. For these types of count variables, the types of graphs and summaries used for continuous variables are often appropriate.
In categorical data each observation falls into one of a number of distinct categories. Thus a categorical variable has a number of distinct categories. Such data are everywhere in everyday life. Some examples of pairs of categorical variables are:
- gender and pet preference between cat and dog
- favourite TV show and favourite holiday activity
- gender and favourite food
- favourite sport and colour of hair (e.g. redhead, blonde, brown, black)
Sometimes the categories are natural, such as with gender or preference between cat and dog, and sometimes they require choice and careful description, such as favourite holiday activity or favourite food.
Initial questions that can motivate an investigation.
The following are some examples that involve collecting, or accessing, or obtaining, data for which considerations of representativeness and sources of variation are of core importance in planning the data investigation, and, in the final phase of the data investigation, interpretation in context.
- A
- A school is planning catering for a (free) end-of-year concert and wants to estimate the number of people who will attend. Should they give a survey to all students or should they survey a subset of students?
- B
- A school would like parents’ opinions on a number of matters that do not lend themselves to simple questions. The school decides to obtain opinions by asking questions in person of a representative group of parents. They are wondering whether to send a message home asking for volunteer parents, or whether to select parents to be interviewed.
- C
- A group of students are interested in investigating the length of the most popular songs. They decide to investigate the top 25 songs on the annual JJJ charts over a number of years.
- D
- When you clasp your hands, which thumb is on top? Most people find that they always have either the left or right thumb on top and that it is very difficult to clasp their hands so that the other thumb is on top. There may be a genetic link in these simple actions. See, for example, http://humangenetics.suite101.com/article.cfm/dominant_human_genetic_traits which includes the following statement:
'Clasp your hands together (without thinking about it!). Most people place their left thumb on top of their right and this happens to be the dominant phenotype.'
A group of students are interested in investigating this.
- E
- How good are people at estimating periods of time? That is, how good are they at estimating a length of time such as 10 seconds?
- F
- Governments and the Cancer Council and other groups run advertisements, especially in summer, to try to get people to protect their skin from the effects of exposure to sun. For example, in November 2009, the campaign for summer 2009-2010 was launched at Bondi Beach, with towels on the beach representing the Cancer Council’s estimates of the number of Australians who would die from skin cancer in the next year. They would like to know if people tend to heed the Slip, Slop, Slap messages, and about differences such as whether adults are different to teenagers with respect to sun behaviour.
- G
- How aware are people of environmental issues? How knowledgeable are they
of relevant facts? - H
- Do people tend to use the lift or stairs in going up at a bus or train station?
What proportion of those going up use the lift? - I
- How long should the green be on pedestrian crossing lights? How long do people tend to take to cross the road at a pedestrian crossing with crossing lights?
The above are examples of just some of the many questions or topics that can arise that involve considering how to collect data, sources of variation, and variation within and across datasets. The examples also involve considerations of summaries of data and how they vary across datasets. Some of these examples are used here to explore the progression of development of learning about data investigation and interpretation. The focus in this module is on planning for data collection, exploring and interpreting variation, and the variation of features of data.
Identifying issues and planning to obtain representative data
In the first part of the data investigative process, one or more questions or issues begin the process of identifying the topic to be investigated. In thinking about how to investigate these, other questions and ideas can tend to arise. Refining and sorting these questions and ideas along with considering how we are going to obtain data that is needed to investigate them, help our planning to take shape. A data investigation is planned through the interaction of the questions:
- ‘What do we want to find out about?’
- ‘What data can we get?’ and
- ‘How do we get the data?’
Planning a data investigation involves identifying its variables, its subjects (that is, on what or who are our observations going to be collected) and how to collect or access relevant and representative data.
Example A: catering for (free) school end-of-year concert
In this example, ideally the school would know what every school family intends to do, and there is no interest in generalising outside the school. The school would most likely request every family to respond to a simple survey asking how many, if any, of each family plan to attend the concert. This type of data collection, in which the aim is to collect information about every member of a population, is called a census. We would probably not think of a form sent to every family of a school being a census, but it is a simple example of one.
If a census is to obtain the required information from every member of a population, and if we are interested only in the information for that population, how can there be any problems with accuracy? The simple scenario above provides some examples. Even with the best of intentions and care, some forms will not reach some families, and some will not be returned. There may be misunderstandings − for example, some families may count their school students in the number attending, and some may not. Changes may occur between the return of the form and the night of the concert. Based on past experience − and past data − the school may be able to allow for these sources of variation in estimating the numbers for catering purposes.
General statistical note
We mostly associate the word 'census' with the censuses carried out by national statistical offices, such as the Australian Bureau of Statistics. These censuses are major undertakings conducted to obtain as complete information as possible on variables that are important for government, industry and the whole community. National censuses aim to obtain population data not only for vital information for future planning and strategies, but also to guide further data collections.
Australia conducts a national census approximately every five years. It is called the Census of Population and Housing. The date of the 16th Australian Census is 9th August, 2011.
The word 'census' comes from the Latin, censere, which means 'to rate', and an essential and first aim of a country’s census is to count − total number of people and numbers in different groupings. This is partly why a census is of the whole population.
It is very important for nations to have accurate census data. The quality of Australia’s census data is highly regarded internationally. What can go wrong in collecting census data? There are many challenges: ensuring everyone is reported on one and only one census form, ensuring every census form is completed and returned, omissions, accidental errors, errors due to language or understanding difficulties, deliberate errors. National offices of statistics use many sophisticated statistical techniques to estimate and cross-check for errors, and to 'allow for' the types of challenges outlined above.
Example B: interviewing for parents’ opinions
Not only would it be very time-consuming to interview all parents of a school, but it would also be very challenging to organise consistent interviews in a reasonable time frame. Choosing which parents to interview to obtain representative opinions is the ever-present challenge of choosing how to conduct a sample survey. A random sample would be obtained by putting all the parents’ names in a hat and selecting the desired number of names from the mixed up names in the hat. This is selecting the names 'at random' to obtain a random sample. If students had identity numbers, another way of choosing a random sample of parents could be to use random numbers to choose students at random and then ask the opinion questions of their parents. Students could simply be numbered in any way and random numbers used to choose a random sample of students, and hence their parents.
General statistical notes on sample surveys
Conducting sample surveys to obtain representative data can be very challenging and complex − which is why there are specialist polling companies and why designing sample surveys is such a large part of the work of government statistical offices.
Conducting a survey by asking people to phone in or register an opinion online is understood to be one of the most unreliable ways of collecting data because the data are representative only of those who want to phone in or respond online! Phoning people at random is better but we must consider aspects such as the time of day and what to do if people refuse to answer the survey.
In the school survey of parents in Example B above, suppose we have carefully chosen a random sample of parents and mailed the survey form to them. There will always be non-respondents. Do we ignore them? It is usually recommended to follow up non-respondents because the original group was chosen randomly and hence are representative, but those who respond without any prompting could be those who are less busy or those with stronger opinions. Note that the amount of attention needed to non-responses tends to be greater when opinions are being sought. If a survey is asking questions about factual matters that do not tend to produce reactions (e.g. 'what is your height?') then whether people respond or not, is less likely to be associated with their responses.
It might be felt that parents’ opinions might vary considerably across the school levels in which their children are. It might be decided to conduct the survey by choosing random parents of students in different school levels, or grouped levels, for example, Years 7-8, 9-10, 11-12. Within each of these groupings, parents should be chosen at random as described above. This is called a stratified random sample; the groupings are the strata.
How many parents should be chosen? If a stratified approach is used, how many in total, and how many from each of the groupings or strata? The formal answers to questions of how many observations to choose can be complex and always depend on what is trying to be achieved. For sampling schemes other than simple random sampling from a very large population, these are questions for statisticians and possibly advanced university students studying statistics to consider. However, one principle that is often used in stratified sampling is to choose more from the strata that tends to have either more people in it or greater variation − in this case, of opinions. As you can imagine, these two (more people and greater variation of opinions) often go hand in hand!
Another type of sampling that is unlikely to be appropriate in Example B but could be appropriate in situations such as sampling households in a very large city, is cluster sampling. The totality of sampling subjects (e.g. households) is divided into many clusters (e.g. streets or blocks); clusters are chosen at random, and all units in the selected clusters are surveyed.
General statistical notes for teachers’ background information
How many parents should be chosen? The formal answers to questions of how many observations to choose are not straightforward and depend on what is trying to be achieved. Such questions are considered at university level, but school students can gain some idea of the effects of sample size through investigation and experimentation.
Decisions about numbers of observations to collect depend on the aims of the data investigation and criteria associated with these aims. For example, it might be desired to estimate a parameter such as a proportion or a mean of a continuous variable. In the case of estimation, the criteria would be expressed in terms of how close we would like to be to the true value, and how confident we would like to be in achieving this desired precision.
In the case of estimating a mean of a continuous variable, even deciding how close we want to be and how confident we want to be in this precision is not sufficient; we also need to have at least some idea of how much the continuous variable tends to vary.
In the case of categorical data and estimating a proportion, although some idea of the true value of the proportion is useful, a conservative approach that assumes nothing about the proportion can be used. The conservative approach can be shown mathematically to assume that the proportion is somewhere around 0.5. For example, to estimate a proportion with reasonably high confidence to within 0.05 of its true value can require up to 400 observations if the true value of the proportion is close to 0.5. Fewer are required if the true value of the proportion is closer to 0 or 1; for example, if the true value we are trying to estimate is 1/3, then we require approximately 350 observations to estimate it with high confidence to within 0.05 of its true value. To estimate a proportion with reasonably high confidence to within 0.01 of its true value can require up to 10,000 observations. To estimate it with reasonably high confidence to within 0.1 can require up to 100 observations.
Estimating to within 0.1 means that if we obtain 55% of our subjects who, for example, have their left thumb on top when they clasp their hands, then all we can say is that we are reasonably confident that the true value lies somewhere between 45% and 65%.
Although students do not need to know anything of the above details until senior or university studies, it is valuable for teachers to know so that they can help in developing and guiding students’ notions of variation across datasets and uncertainty in thinking beyond the data 'in hand' to a more general situation of which we may consider the data to be representing.
Note that the true value of the proportion referred to above is for the general situation or population for which our data are representative.
Example C: length of songs
Obtaining data for the top 25 of the JJJ charts for a number of years is taking a census of the top 25 in that chart for the selected years. It is not a random sample of songs produced or played. Could it be considered to be representative of top 25 (JJJ) songs beyond the years of collection? Could it be considered representative of popular songs with respect to any question? For example, could such a dataset be considered representative of the lengths of popular songs − if only for those years? There is no way of knowing, is there? In any reporting it must be very clear that the songs considered are the top 25 JJJ songs in each of the years selected, and generalisations should be avoided.
Example D: which thumb is on top?
Almost everyone finds that when they clasp their hands, the same thumb tends to be on top and it is very difficult to clasp such that the other thumb is on top. This observation, plus scientific articles such as the one at http://humangenetics.suite101.com/article.cfm/dominant_human_genetic_traits, do tend to indicate that it is a characteristic an individual is born with − a genetic trait. To estimate the proportion of people who have their left thumb on top when they clasp their hands, can we just select any group? If there is no information about how such a genetic trait might be linked with other traits, how can we choose a representative dataset, and of what do we want to be representative? In a situation like this in a real data investigation, we might collect data on other variables to investigate the possibility of links between thumb on top and other variables such as gender, handedness etc.
Although we have to choose people to observe, and hence, as in Example B, we are choosing who to 'survey', this type of investigation is not usually thought of as a 'survey' because we are observing characteristics of people, and it is not clear whether following types of procedures used for surveying people is going to be any more representative with respect to the question of which thumb is on top, than an arbitrary sample!
Example E: estimating a length of time
How well do people estimate a length of time such as 10 seconds or a minute? And how should they be asked to estimate it? One way is to use a stopwatch and start the stopwatch and the subject on 'go' with the subject calling 'stop' when they think the time period is finished. Their estimate is the time recorded by the stopwatch. The variable is the guessed or estimated time and the observations are recorded per person.
Example F: Sun Protection Survey
How aware are adults and teenagers of the need for sun protection, and do they act on any such awareness? Does the Slip, Slop, Slap message have any effect? The National Sun Protection Survey of 2006-2007 was the second such survey; the first was conducted in 2003-2004. The study is funded by the Cancer Council Australia and the Australian Government through Cancer Australia. Trying to obtain accurate and consistent information about people’s sun protection habits is very challenging because people themselves can be quite inconsistent in behaviour of this type, and it may depend on a number of factors as well as on interpretation of questions. The 2006-2007 survey reached respondents through phone interviews conducted on Monday and Tuesday evenings during summer. The interviews focussed on weekend behaviour in summer, and also recorded whether the person was an adolescent or an adult, and in which state they lived. These questions give data for three categorical variables for each person: sun protection behaviour on the weekend; age group; and location (state where live).
Notice the methods used to try to obtain as representative a group as possible, and to try to obtain consistency in conditions of the questions. Random phone dialling is used; phone calls are made in weeknight evenings so that those at home are representative of the whole population. Making the calls on Mondays and Tuesdays serves two purposes: people are less likely to be out on those weeknights, and the closer to the weekend, the better it is for achieving accurate memory. Asking about weekend behaviour helps in obtaining consistency of conditions as working conditions are highly variable. Also weekend activities are more likely to involve the outdoors across a wide range of people.
Example G: Environmental awareness and knowledge
Notice that there are two aspects in this topic as people’s awareness is not the same as people’s knowledge. Hence the survey questions will need to cover both aspects, will need careful thought and the survey will take at least a few minutes to complete. Should a survey like this be conducted in person or not? Conducting surveys 'remotely', whether by paper or online is less expensive and can reach more people but the questions must have no possibility at all of any ambiguity and there is the problem of the non-responses, particularly from the representative point of view. This is why some survey designs use a follow-up tactic on non-respondents.
Survey questions must be absolutely clear to all respondents. Unless it is known exactly what each question means to each respondent, survey data are useless.
If a survey is conducted in person, it is still best to have the questions on paper so that exactly the same questions are asked in exactly the same order. Just as much care is required in preparation and trialling of the questions beforehand. The advantages of 'in-person' surveying are that it tends to be easier for people to respond and hence the response rate tends to be better; reasons for non-response can sometimes be noted; any unforeseen ambiguities can be corrected; extra comments can be noted; and the overall effort for respondents tends to be less, leading to more and better quality data.
A question such as 'are you concerned about environmental issues?' can be a leading question. Many people would be reluctant to say no, or even don’t know. A better way of asking about concern could be to ask someone to rate their degree of concern for environmental issues from 1 to 5 of increasing concern with 3 neutral. (1 being very unconcerned, 2 unconcerned, 3 neutral, 4 concerned and 5 very concerned).
There are many considerations in designing a survey like this; some are discussed in general below.
General statistical notes on survey questions
In a survey as in Example G, knowledge (e.g. of environmental issues) can be surveyed by factual statement questions and asking for a true, false or don’t know response. A mixture of true and false statements is advisable, and it is sometimes recommended to commence with a statement that is easy to answer to help people get started.
As mentioned in Example G, statements or questions that are difficult to disagree with, can place pressure on respondents as well as potentially distort information. For example, in the context of Example G, a question such as 'do you agree that the media could do more to create awareness of important environmental issues?' and 'Do you recycle as often as you can?' are unlikely to provide accurate or useful information.
Exercise: Suggest ways questions on these issues could be phrased in order to obtain accurate information.
In a survey, an open question is one in which respondents are allowed to answer in their own words; a closed question is one in which respondents are given a list of alternatives from which to choose their answer. Usually, the latter form offers a choice of 'other' in which the respondent is allowed to fill in the blank. Both types of questions have strengths and weaknesses.
To show the limitation of closed questions, consider Example G and how to ask what people think are the most important environmental problems (or challenges). This could be asked by an open or closed question, with the latter consisting of a list for respondents to choose the most important or to rank importance.
If closed questions are preferred, they first could be presented as open questions to a test sample before the real survey, and the most common responses could then be included in the list of choices for the closed question. This kind of 'pilot survey,' in which various aspects of a study design can be tried before it’s too late to change them, should always be conducted.
The biggest problem with open questions is that the results can be difficult to summarise. If a survey includes thousands of respondents, it can be a major chore to categorise their responses. Another problem is that the wording of the question might unintentionally exclude answers that would have been appealing had they been included in a list of choices (such as in a closed question).
There are advantages and disadvantages to both approaches. One compromise is to ask a small test sample to list the first several answers that come to mind, then use the most common of those. These could be supplemented with additional answers that may not readily come to mind.
General statistical notes on survey confidentiality/anonymity
People will often answer questions differently based on the degree to which they believe they are anonymous. Because researchers often need to perform follow-up surveys, it is easier to try to ensure confidentiality than anonymity. In ensuring confidentiality, the researcher promises not to release identifying information about respondents. In an anonymous survey, the researcher does not know the identity of the respondents.
Such considerations are also very important in a nation’s census data. In Australia, the Census Information Legislation Amendment Bill 2005 amended the Census and Statistics Act 1905 and the Archives Act 1983 to 'ensure that name-identified information collected at the 2006 Census and all subsequent censuses, from those households that provide explicit consent, will be preserved for future genealogical and other research, and released after 99 years' http://www.aph.gov.au/library/Pubs/BD/2005-06/06bd071.htm . This Bill was essentially a compromise between the needs of history and the need to obtain accurate census data.
Example H: Lift or stairs?
Information about people’s behaviour can be important in designing public facilities. Bus and train stations need to be able to cope with many people in peak hours. Most big bus stations have stairs and lifts − not just for underground bus stations, but also linking pedestrian overpasses to platforms, just like train stations. As well as information about numbers of people using the stations at various times, estimates of the proportion of users who tend to use the stairs or lifts could be valuable input to the design process.
To collect relevant data, certain times would need to be chosen, and numbers of people using stairs or lifts to go up or down in those time periods recorded. Although this would probably be regarded as an observational study rather than a census or a survey or an experiment, notice that there are still choices to be made to obtain representative data − namely, the times for observation. If peak periods are of concern, then these would be chosen. Notice that the times would not be chosen at random; rather the observation periods are the conditions under which the observations are made.
Example I: How long should the green last?
Like Example H, this topic would be motivated by design issues. The length of green for a set of pedestrian lights is clearly dependent on the width of the crossing. The width of the crossing and information about walking speeds could be used, but what is important here? Is it the average walking speed? No, because some allowance needs to be made for slower people − that is, variation in walking speeds must be taken into account. Also walking speeds in crossing a road might be different to walking speeds in general. Hence data on how long people take to cross a road of in a certain type of locality (e.g. in the city, at a school crossing) could then be valuable information for crossings of that type, allowing for different widths of crossings.
How much should be allowed for variation in times to cross? That is, how much allowance for variation should there be?
As in Example H, this would be an observational study, but with control over the conditions for the observations. In studies such as these, providing full details of the how, when and where of the data collection, together with descriptions of the circumstances to explain any choices of conditions, is essential for sound interpretation of the data, and for the study to be extended or repeated in the future if this becomes desirable.
Variation within and across datasets
Statistics is the science of variation and uncertainty − the science of investigating, identifying, measuring, estimating, describing, modelling, attributing, interpreting, minimising and allowing for, variation and uncertainty.
In the data strand, we focus more on the variation aspects. We will consider some aspects of variation in the above examples.
Census data
A census aims to obtain information from a whole population. Questions of representativeness do not arise if we have the required information on the whole population. In reporting and using census data, identifying, describing, investigating and attributing variation are all important, but in principle we do not have to consider variation and uncertainty due to sampling − that is, due to having a subset of a whole population, or to having a set of observations that are representative in some way of a more general situation.
This is 'in principle' because in large and complex censuses, such as national censuses, mistakes, omissions, non-responses or even non-contacts must be investigated, modelled, estimated and allowed for. Such issues are very complex and challenging, requiring very advanced statistical expertise and information. Minimising the risk of these difficulties also requires significant government and statistical knowledge and expertise, with associated thorough and high quality planning.
Example A includes, on a small scale, some of these challenges of a census. All families need to be contacted; the question(s) must be clear to avoid unintentional mistakes; allowance must be made for mis-reporting (in the case of Example A, this is essentially changes of plans after returning the form); and non-returns of forms requires estimation of the unknown intentions of non-respondents. In Example A, the effects of these issues are probably not great − after all, there is still estimation required of the amount of catering required even if the attendance is known accurately! But the example does provide at least some idea of the enormous challenges (and expense) of a national census. But the need for, and value of, high quality national census data for every aspect of strategic planning for a country, cannot be sufficiently emphasized.
Classroom Activity: Explore the Australian Bureau of Statistics website on Census data http://www.abs.gov.au/websitedbs/d3310114.nsf/home/census+data Find the report for your location, and identify at least two planning issues for your location for which the Census data provides valuable information.
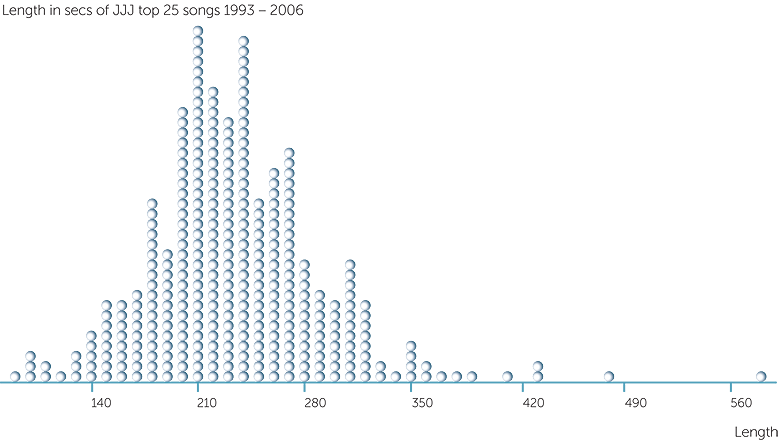
In Example C, the dataset can be regarded as a census of the top 25 songs on the JJJ charts for the years for which the data were collected. The only mistakes or omissions here would be collecting ones. The dotplot and stem-and-leaf plot below show the lengths (in seconds) of the JJJ top 25 songs for 1993-2006.
Stem-and-leaf of Length
Leaf Unit = 10
| 1 | 0 | 9 | ||
| 17 | 1 | 0000122234444444 | ||
| 82 | 1 | 55555555556666667777777777777778888888888888888899999999999999999+ | ||
| (150) | 2 | 00000000000000000000000000000000001111111111111111111111111111111+ | ||
| 118 | 2 | 55555555555555555555666666666666666666666667777777777777777777888+ | ||
| 41 | 3 | 0000000000011111111112222244 | ||
| 13 | 3 | 55556688 | ||
| 5 | 4 | 022 | ||
| 2 | 4 | 6 | ||
| 1 | 5 | |||
| 1 | 5 | 7 |
The lengths vary from 90 seconds up to an unusually long song (compared to the rest) of 570 seconds (to the nearest 10 seconds). The second longest song is 460 seconds. However almost all the songs are between 2 and 6 minutes long, and most are between
3 and 5 minutes.
Which do you think would be larger for these data? The average or the median? Answer: the average because of the few values that are much larger than the rest of the values; in fact, the average length is 234 secs and the median is 229 secs.
Sample data: categorical data
For categorical variables − and hence categorical data − we are interested in relative frequencies or proportions of the different categories. If we have census data, we can simply report percentages or proportions for a country. If we have sample data that are representative of some general situation, we are interested in using the sample data to estimate proportions for the more general situation.
Hence we need some idea of how much variation we could get across different samples of data and hence how much variation we could get in our estimate of the proportion in the more general situation. Involved in these questions are also the questions of:
- whether our sample(s) of data are representative of the general situation − or, from another viewpoint, of what can we consider our sample(s) of data to be representative?
- can any variation we observe be attributed to, or explained by, some other variables?
Example D: Which thumb is on top?
When individuals clasp their hands, either the left or right thumb tends to be on top and it is very difficult to clasp one’s hands with the other thumb on top. It is claimed that this is a genetically-linked characteristic, just as whether people can roll the sides of their tongues or not is a genetic characteristic.
So it should be reasonably simple to estimate the proportion of people in general who have their left thumb on top when they clasp their hands. Left thumb on top is claimed to be genetically dominant ( see, for example, http://humangenetics.suite101.com/article.cfm/dominant_human_genetic_traits). That is, we do not have to worry about the circumstances of collecting the data and any reasonably random sample − perhaps avoiding close relatives within the sample − should be reasonably representative.
But how many observations should we collect to estimate the proportion of people who place their left thumb on top and how much will our sample proportion vary over different samples?
In a group of 203 people, the following barchart shows how many had their left thumb
on top.
thumb on top
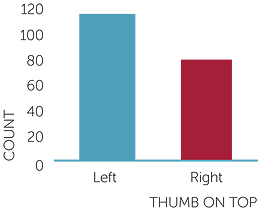
The percentage of these 203 people with the left thumb on top was approximately 57%.
Whatever the true % overall for everyone is − that is, whatever the % of people who have their left thumb on top when they clasp hands − we are not going to get this % when we take a sample of people no matter how representative our sample is. Indeed, it is because a sample is random that we will not get the same %. Variability across samples of data is called sampling variability. How great is it likely to be?
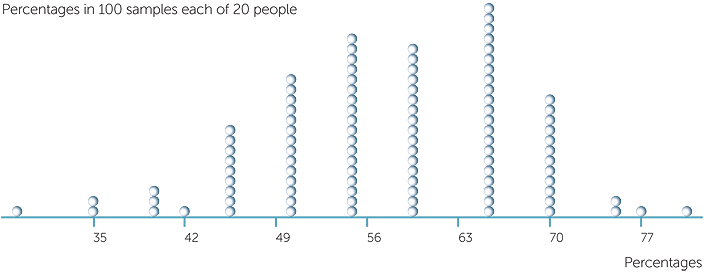
Assuming that 57% is the true % of people overall who have their left thumb on top when they clasp hands, below are a dotplot and a stem-and-leaf plot of the %’s in 100 different samples of people, with each sample consisting of 20 randomly chosen people. (See Appendix 1 for how to generate such data using Excel.)
Stem-and-leaf of Percentages
Leaf Unit = 1.0
| 1 | 3 | 0 | ||
| 3 | 3 | 55 | ||
| 6 | 4 | 000 | ||
| 15 | 4 | 555555555 | ||
| 29 | 5 | 00000000000000 | ||
| 47 | 5 | 555555555555555555 | ||
| (17) | 6 | 00000000000000000 | ||
| 36 | 6 | 555555555555555555555 | ||
| 15 | 7 | 000000000000 | ||
| 3 | 7 | 55 | ||
| 1 | 8 | 0 |
The percentages above vary from 30% to 80%!
The above samples of size 20 have been obtained by simulation. But data on how people clasp their hands are quite easy to collect quickly and from many people. Ask each student in the class to ask 20 people to clasp their hands and report how many had their left thumb on top. Use a dotplot or stem-and-leaf as above to show how much variation there is in the percentages collected by the students.
So if we are trying to estimate the proportion of all people who have their left thumb on top in clasping hands, we should pool all the data we can. Suppose we collect 200 observations. Below is a stem-and-leaf of 100 samples, each of 200 randomly chosen people, with the overall percentage of people who place their left thumb on top in clasping hands, being again 57%.
Stem-and-leaf of Percentages
Leaf Unit = 1.0
| 1 | 4 | 8 | ||
| 5 | 5 | 1111 | ||
| 19 | 5 | 22222233333333 | ||
| 34 | 5 | 444444455555555 | ||
| (23) | 5 | 66666666666677777777777 | ||
| 43 | 5 | 88888888899999999999 | ||
| 23 | 6 | 00000000001111 | ||
| 9 | 6 | 222223 | ||
| 3 | 6 | 55 | ||
| 1 | 6 | 6 |
In these 100 samples, each of 200 people, the percentages still vary from 48% to 66%! And if we took another 100 samples, each of 200 people, we would not get exactly the same variation in the %’s.
Let’s see what can happen if we ask 1000 people. Below is a stem-and-leaf plot of the percentages of 1000 people in 100 randomly chosen samples − each with 1000 people − assuming still that over all people in general, 57% have their left thumb on top when they clasp hands.
Stem-and-leaf of Percentages
Leaf Unit = 0.10
| 1 | 53 | 0 | ||
| 2 | 54 | 0 | ||
| 17 | 55 | 000000000000000 | ||
| 40 | 56 | 00000000000000000000000 | ||
| (20) | 57 | 00000000000000000000 | ||
| 40 | 58 | 00000000000000000000000000 | ||
| 14 | 59 | 000000 | ||
| 8 | 60 | 00000000 |
We see that in these 100 samples of 1000 people, the %’s with left thumb on top range from 53% to 60%; not as variable as in the samples of 200 people and certainly much less variable than in the samples of 20 people.
Clearly we have to be very careful in reporting %’s, and clearly we need a lot of data to be able to accurately estimate proportions. We need to always report how many observations were collected, and how they were collected, and can say only what the % was in our data.
Classroom Activity: Whether people can curl the sides of their tongues is a well-known genetic variable. Students could collect small amounts of data (for example, samples of size 20) to investigate the sample variability of the proportion of people who can curl the sides of their tongues.
Data for Example H below illustrates further the variability in proportions across samples of data of categorical variables
Example H: lift or stairs to go up?
At a certain bus station, data were collected on a normal day during both the morning and evening peak times with the aim being to try to estimate what proportion of people going up choose to use the lift rather than the stairs. The data are below, presented in the form of two-way tables for each of the peak periods − morning and evening.
Table of choice of lift or stairs
for going up or down: evening peak
| Down | Up | Total | |
| Lift | 76 | 300 | 376 |
| Stairs | 420 | 213 | 633 |
| Total | 496 | 513 | 1009 |
Table of choice of lift or stairs
for going up or down: morning peak
| Down | Up | Total | |
| Lift | 45 | 222 | 267 |
| Stairs | 204 | 210 | 414 |
| Total | 249 | 432 | 681 |
Overall, in these data, 522/945 = 0.5524 (or 55.24%) of the people going up chose to use the lift, while only 121/745 = 0.1624 (or 16.24%) of the people going down chose to use the lift. In the evening, these %’s were 58.5% and 15.3%; while in the morning peak, these %’s were 51.4% and 18.1%. Before you are tempted to say that more people tend to take the lift to go up in the evening, but more tend to take the lift down in the morning (more tired in the evening going up, but more in a hurry going down in the morning?), remember how much these %’s can vary even with such large numbers of observations.
Below are dotplots of the percentages choosing the lift to go up for 500 people in the evening and 430 people in the morning if the true %’s in general are 59% for the evening and 51% for the morning.
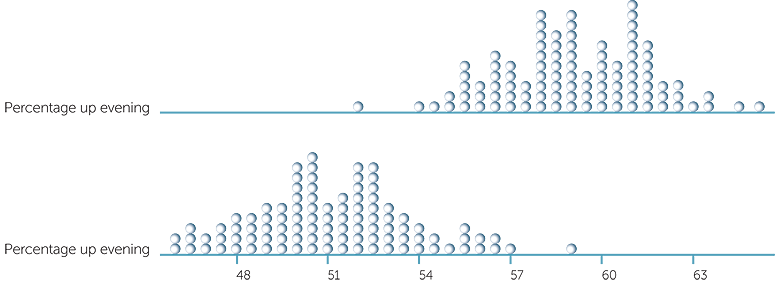
Notice that it is possible to get %’s that are very close together and even to get %’s in reverse with a slightly greater % of people in the morning than the evening choosing the lift to go up. So for the observed data in the tables, we can quote the %’s but say that there is some indication that the morning behaviour is different to the evening behaviour − but we’d be cautious.
What can happen if the true percentages are closer together? Below are dotplots of the percentages choosing the lift to go up for 500 people in the evening and 430 people in the morning if the true %’s are 58% for the evening and 52% for the morning.
So we see that there’s more chance of observing %’s that are close together or with the morning % greater than the evening %.
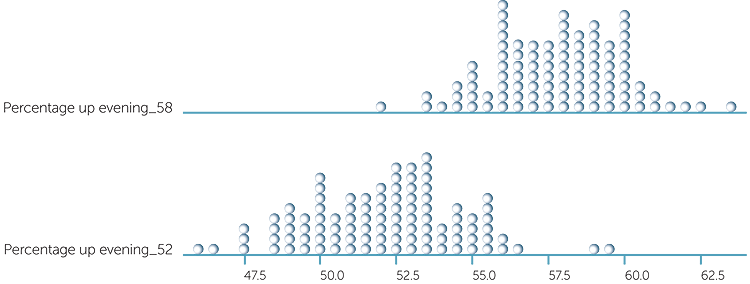
Does the same sampling behaviour tend to happen with the smaller %’s of 15% and 18%? These are the observed %’s for the people who choose to use the lift to go down in the evening and morning peak hours. These are much closer together than the %’s considered above. Let’s see what can happen if these are the true %’s in general. Below are dotplots of the %’s using the lift in 100 samples of 500 people going down in the evening and in 100 samples of 250 people going down in the morning, assuming that the true %’s in general are 15% and 18% respectively.
So there’s a lot of overlap as we would expect with the true %’s so close together. Notice how much more variable the %’s are for the morning groups because there’s only 250 in each group compared with 500 in each of the evening groups.
So based on the single observed dataset in the tables above, we could report the %’s who chose to use the lift to go down in the morning and evening peak periods but our comment should be that they are very close!
The examples above are of categorical data with just two categories so that looking at the variation across samples could focus on looking at the variation in the percentages of one of the categories. In Example D, there was one categorical variable; in Example H there were three categorical variables (peak period, direction, choice of lift or stairs) and the interest in Example H is not just in individual %’s but also %’s within different categories and in comparing these %’s over the two peak periods.
For categorical variables with more than two categories, the %’s in each category vary across samples in a similar way to the above examples. A dynamic illustration of this variation for different sample sizes can be found in the Categorical Variables section of http://www.censusatschool.org.nz/2009/informal-inference/WPRH/ . This dynamic illustration is of a barchart of the %’s using different types of transport to school in Auckland. The samples of different sizes are chosen at random (with replacement) from a large dataset obtained through the Census at School project in New Zealand.
Sample data: continuous data
For samples of continuous data we are interested in describing the variation of values within a sample (just as we are if we have continuous data in a census) and in considering how much variation there could be across samples collected in the same circumstances.
Example E: Estimating a length of time
Below is a dotplot of the guesses (in seconds) of 10 seconds for 120 people chosen at random. Each person was asked to guess 10 seconds from the time 'go' was said and their guess was recorded by a stopwatch. For each person there was no practice or repetition − this was their first and only guess at 10 seconds in this investigation.
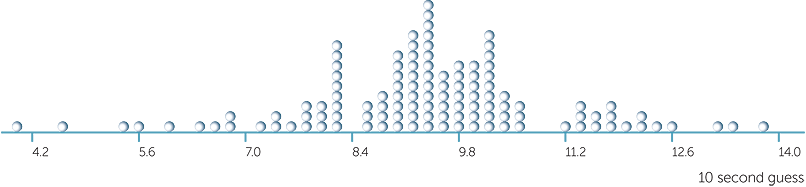
The guesses are highly variable, ranging from about 4 seconds up to just under 14 seconds. Most seem to be under 10 seconds.
How much variation could we see across such samples? There are a number of sources of variation in this example in a real study: variation from person to person; variation for each person, as an individual is not going to guess exactly the same length each time they try; and variation due to measuring the length of the guess. Another possible source of variation is variation due to the conditions of the experiment although these can be kept as constant as possible.
These types of variation − from person to person, for each person and due to measurement − can be modelled statistically, but let’s just focus on variation due to sampling by taking random samples from this set of values. That is, we are going to consider that each of these 120 values is equally likely to be chosen, and we are going to choose from these 120 values at random. So that the chance of getting each value stays the same, we are going to sample with replacement. That is, if a value is chosen, it is not removed from the set of values from which we can choose.
This simulation can be carried out by writing the observed values on 120 different pieces of paper, putting them in a container, and choosing a number of pieces of paper at random from the container, replacing each piece of paper before the next 'draw' after recording its value. See Appendix 1 for how to obtain simulated samples using Excel. This type of sampling is called re-sampling (with replacement).
Below are dotplots of the 120 values and 5 samples, each of 20 values, chosen at random (with replacement) from these 120 values.
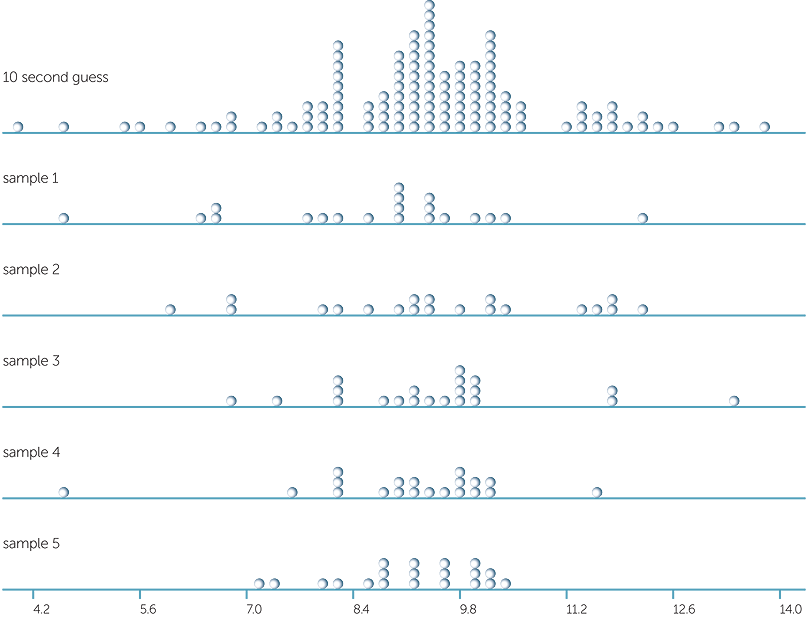
The variation across the 5 samples that we can see in the above is entirely due to random sampling, and we see that there can be quite a lot of variation due to sampling.
The ranges in the 5 samples vary, with two having their minima about 4.5 seconds, and the rest about 6 seconds. One has its maximum value about 13.5 seconds, and the others about 11.5 to 12 seconds.
The averages (to the nearest 0.1 sec) of these 5 samples are: 8.66 secs, 9.49 secs, 9.46 secs, 9.10 secs, 9.16 secs.
How much variation could there be in the averages of samples of size 20 from these 120 values? The average of the 120 values is 9.4 secs (to the nearest 0.1 sec). Below is a dotplot of the averages of 100 samples of size 20 chosen at random (with replacement) from the 120 values.
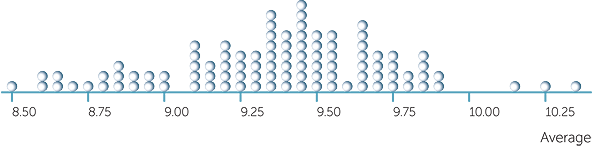
We see that there can be a lot of variation in the average.
What can happen if we take larger samples? Below is the above dotplot repeated together with a dotplot of the averages of 100 random samples each of size 80 (all samples taken from the original 120 values).
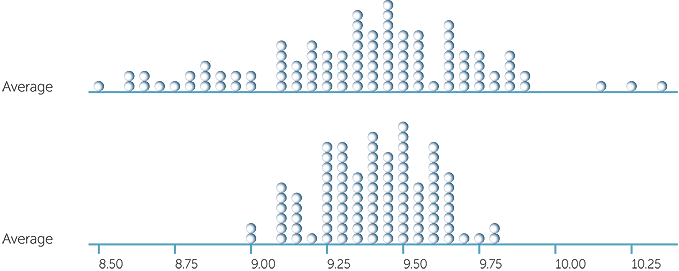
We see that there is much less variation in the averages of the samples of size 80 compared with the samples of size 20, just as there was much less variation in the sample proportions for categorical data as we took larger and larger samples.
This is why we take as many observations as we can to estimate quantities such as proportions and means.
Classroom Activity: The focus of the above example is on sampling variability. The original set of 120 observations illustrates considerable variation across different people in estimating 10 seconds. Students can investigate variability of individuals in estimating 10 seconds by collecting a number (for example, 10) of observations for each person. They can then compare the variability of individuals’ guesses across individuals. They could also calculate the average guesses and look at the variation in those, and their best (that is, closest to 10 seconds) guesses and look at the variation in the best guesses.
Example E: Estimating a length of time:
comparing males and females
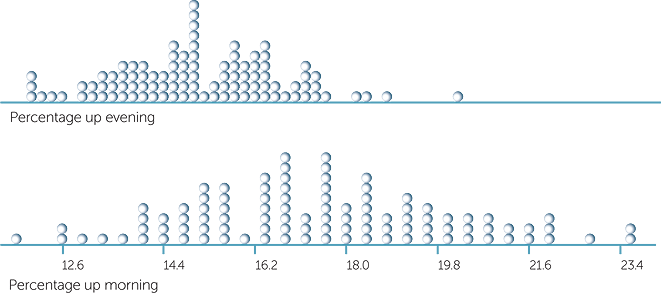
In the data for the guesses (in seconds) of 10 seconds for 120 people chosen at random, there were 60 females and 60 males. Note that this also means that a fixed number of males and females were chosen at random rather than the whole 120 people. Below is a dotplot of the guesses separated into males and females.
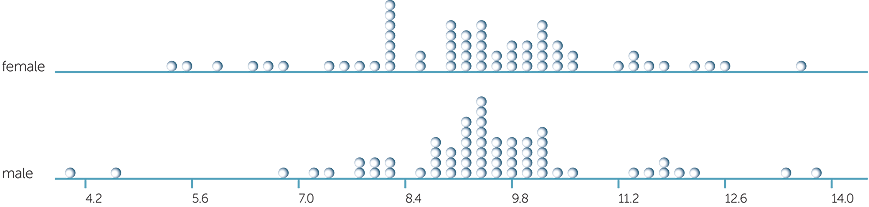
The averages are very close: they are 9.35 secs for females and 9.44 secs for males. Having seen how much averages can vary across samples just because of sampling variability, we are definitely not going to say that these data indicate that males and females differ on average in their guesses of 10 seconds! There is also not much difference in the variability in these two sets of 60 observations: there are 2 males who greatly underestimated 10 secs, with the guesses of most of the males in this group perhaps rather more bunched than those of most of the females. But these comments are about these particular two groups of observations. Now that we’ve seen how much variation there can be due to sampling, we know to be careful in generalising from these data.
General statistical notes on information from data
We obtain data in order to obtain information. A census aims to obtain the total information for a population, usually of a country. In obtaining sample data, whether of a population or under certain conditions, we aim to obtain representative data, because we need representative data to be able to obtain representative information. Obtaining representative data means our observations must be a random sample − by choosing randomly if we are dealing with a population, or by taking observations randomly under the same circumstances if we are dealing with an observational or experimental situation.
Because practicalities often govern what can and can’t be collected, we often have to assume that our data are representative of a more general situation. This is why it is of the greatest importance to describe exactly how data were obtained or collected. Also, data can be considered representative in considering some questions, but not for others.
General statistical notes on generalising from data samples: statistical inference
The above examples clearly show how much care is needed in using samples of data to generalise to a situation of which the data are representative. This is called inferring from data. Statistical inference provides principles and methods for inferring from data that take account of the variation due to sampling. Because these methods are developed from clearly stated assumptions and models of variation, the methods can be applied and interpreted universally. The models make use of theory and mathematical models of variation that are studied at university level. But examples that involve comparing different datasets collected under the same conditions, or obtained by simulation as above, help in understanding how much variation can happen across samples and how much quantities such as percentages and averages can vary. This helps in being cautious in generalising from data.
The above examples illustrate that what is needed is to be able to say how much the true proportion or true mean could vary from what we get in just one sample of data (that is, our sample proportion or sample mean). That is, what is needed is to be able to give an interval which we are fairly confident will include the overall proportion or mean of the general situation of which our data are representative. How to do this and how to use it is beyond this level, but if you now read in the media, a report such as 'the percentage of adults who agree with …… is estimated to be between 54% and 59%' then you know that the investigators are doing what they should do, namely, making a statistical inference that allows for sampling variability.
The quantities calculated from data that have been considered in the above examples are proportions (or percentages) for categorical data, and averages for continuous data. These are not necessarily the only quantities of interest, as the following example shows.
Example I: How long should the green last
for a pedestrian crossing?
In deciding how long to make the green for any particular pedestrian crossing, the traffic conditions and width of the crossing need to be considered, but what should be considered about the crossing speed of pedestrians? Should we consider the average crossing speed of pedestrians? Should we consider the range of types of pedestrians who use that crossing? These two questions immediately raise two sources of variation: variability in crossing speeds and variability in types of pedestrians. But whatever types of pedestrians we consider, we don’t want to set the length of green to average crossing speed. What is more likely to be useful is to estimate the crossing speed that most users can manage from a standing start. Hence good information about the variability of crossing speeds is needed. It might be decided to estimate the crossing speed that 95% of people can manage from a standing start, so that the flashing red signal caters for everyone from a standing start. Then the criteria for the decision about length of the flashing red also need to be chosen!
Classroom Activity: collect data from a number of pedestrian lights measuring the length of the green and the length of the flashing red to investigate the variation in these lengths across different pedestrian crossings and the relationships between the length of green and the length of flashing red.
Can we seek to explain variability?
In some of the examples above, there is interest in investigating comparisons of data on one variable with respect to one or more other variables. For example, do commuters tend to be more likely in the morning or evening peak to use a lift instead of stairs to go up at a bus station? Are males better at guessing lengths of time than females?
This is investigating if a variable is affected by others. Looking at this from another point of view, we are often interested in investigating whether a variable is affected by others, and if so, to what extent. That is, we are often interested in trying to explain at least some of the variability in data by investigating if other variables may be affecting the data. For example, if which thumb is placed on top in clasping hands is claimed to be genetically linked, then we might wonder if males tend to be different to females, or if left-handed tendencies might be associated with this tendency. That is, we might seek to explain some of the variability across individuals by investigating if there are differences between males and females, and left- and right-handers.
For aspects such as measuring reflexes or guessing time periods, we might wish to investigate whether any or all of age, gender or different conditions affect the result. For example, does listening to music affect people’s ability to guess periods of time or their reaction times? Experiments or observational studies or a mixture of observation and experiment could be designed to investigate these issues. There will always be sampling variability, and almost always at least some natural variability due to variability within and across people and/or natural conditions. But statistical methods are developed to ask if some of the observed variability in the data can be attributed to other variables.
Some general comments and
links from F-7 and towards year 9
From F-7, students have gradually developed understanding and familiarity with concepts and usage of the statistical data investigative process, types of data and variables, types of investigations and at least some types of graphical and summary presentations of data. In developing these, considerations have increasingly arisen of the need for representative data, and of describing and/or allowing for variability within and across datasets.
In order to understand how to interpret and report information from data, students need to develop at least some understanding of the effects of sampling variability. This also helps in developing understanding of the need for formal statistical inference, even if the methods, results and processes of statistical inference are not introduced until senior or tertiary levels. Statistical inference also requires that data be representative of a population or general situation with respect to the questions or issues of interest.
Hence this module has discussed the challenges of obtaining representative data, emphasizing the importance of clear reporting of how, when and where data are obtained or collected, and of identifying the issues or questions for which data are desired to be representative. The module has also used real data and simulations, including re-sampling from real data, to illustrate how sample data and data summaries such as sample proportions and averages can vary across samples.
As in Years 4-7, the examples of this module again illustrate the extent of statistical thinking involved in all aspects of a statistical data investigation, in particular in identifying the questions/issues, in planning and in commenting on information obtained from data.
Questions of planning to obtain representative data to investigate everyday questions and issues involving a number of variables are considered further in Year 9, along with developing further skills in exploring, understanding and interpreting data. These build on the greater emphasis in this module on recognising, exploring and interpreting variation within data and across datasets. As in Years F-8, concepts are introduced, developed and demonstrated in contexts that continue the development of experiential learning of the statistical data investigation process.
To use Excel to generate random data, requires the add-in of Data Analysis under Tools.
To use Data Analysis under Tools to generate a number of random samples of data on a categorical variable with a given probability for the category of interest, choose Random Number Generator. For Number of Variables, enter 1. For Number of Random Numbers, enter the number of different samples you want to generate − for example, 100 has been used in many of the examples of this module. For Distribution, choose Binomial. Under the Parameters that appear for Binomial, the p Value is the proportion you wish to assume as the true (or overall population) proportion, and the Number of trials is the size of the sample you wish to generate (for example, you might wish to consider samples of 20 people). The output range needs to be a single column of the same size as the Random Number you chose. The output will consist of a set of numbers out of the Number of trials, so divide by the Number of trials to obtain the simulated proportions.
To use Data Analysis under Tools to generate a number of random samples of data from a given set of values (that is to re-sample from a given set of data), the original data needs to be in a column, with a second column consisting of 1/(number of observations) in each cell. As this second column must sum to 1, you might need to slightly adjust values you enter to ensure this. Choose Random Number Generator. In Number of Variables, enter the number of samples you wish to generate. In Number of Random Numbers, enter the size of the samples. In Distribution, choose Discrete. In Value and Probability Input Range, give the column in which you placed the original data, and the column in which each value is equal (allowing for perhaps a slight adjustment) and sum to 1. In Output Range, give a range of number of columns being the chosen number of samples, and the size of each column being the chosen sample size.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

