The Improving Mathematics Education in Schools (TIMES) Project
- Substitution into an algebraic expression
- Solving linear equations
- Arithmetic with whole numbers, fractions and decimals.
A formula is a way of relating different quantities using algebra. The well-known formula
![]() A = πr2
A = πr2
relates the area A of a circle to its radius r. The formula expresses symbolically the fact that to find the area of a circle, we square the radius and multiply by the number π. This formula relates two variables A and r. We can use the formula to find the area A given the radius r, or we might wish to find the radius given the area.
Euler’s formula
![]() V − E + F = 2.
V − E + F = 2.
connects the number of edges E, the number of vertices V and the number of faces F in a convex polyhedron provided the polyhedron exists. For example, for a cube, E = 12, V = 8 and F = 6. This formula relates three variables. Given values of any two of these variables, we can use the formula to find the third.
Formulas are used in Science, Engineering, Medicine, Economics and many other fields. Scientists often aim to find relationships between physical quantities and express this relationship as a formula.
Famous examples include the remarkable E = mc2, which relates mass m and energy E via the speed of light c. In this equation, c is a fixed constant, while E and m can vary.
Newton discovered the formula for the gravitational force between two objects with masses m1 and m2 separated by a distance r to be
![]() F = G
F = G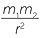
where G is a constant known as the universal gravitation constant.
As well as connecting quantities, formulas allow us:
- to find one quantity given the values of the other connected quantities,
- to see how one quantity changes as the other connected quantities change.
For example in the formula A = πr2, A increases as the square of r, while in the formula F = G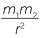
F decreases as r increases. This last formula is sometimes referred to as an ‘inverse square law’.
A list of some of the formulas you might come across in the F-10 Australian Curriculum and also some that are commonly used in the senior years of mathematics and other fields appears in the Appendix. They might be useful in the construction of questions on formulas.
Formulas, variables, numbers and constants
Formulas generally contain pronumerals that can take different values. These are called variables like E and m in the formula E = mc2, constants like G in the formula F = G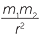 and numbers like π in the formula A = πr2.
and numbers like π in the formula A = πr2.
Many of the formulas that we are dealing with have a single variable on the left-hand side of the equal sign. This variable is called the subject. For instance, in the formula E = mc2, the variable E is the subject and in the formula A = πr2, A is the subject.
A formula like Euler’s formula does not have a subject but can be easily rearranged to make one of the three variables the subject.
If the values of all the variables except the subject of a formula are known, then we can find the value of the subject by substitution.
EXAMPLE
Find the value of the subject when the pronumerals in the formula have the values indicated.
![]() m =
m = 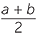 , where a = 12, b = 26
, where a = 12, b = 26
Solution
| m | = 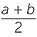 |
|
=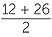 |
||
| = 19 |
EXAMPLE
The formula for the circumference C of a circle of radius r is C = 2πr. Find the value of C when r = 20
| a | in terms of π | b | correct to 2 decimal places. | ||||||
|
Solution |
|||||||||
| a | C = 2πr = 40π | b | C | = 40π | |||||
| = 125.663... | (using a calculator) | ||||||||
| ≈ 125.66 | (correct to 2 decimal places) | ||||||||
Substitution into a formula resulting in an equation
When the variable whose value is to be found is not the subject of the formula, we can first substitute into the equation and then solve the resulting equation.
The chosen units of measurement are always important. The units must be consistent.
EXAMPLE
For a car travelling in a straight line with initial velocity u m/s and acceleration a m/s2, the formula for the velocity v m/s at time t seconds is v = u + at.
a![]() Find the initial velocity if a = 2, v = 15 and t = 7.
Find the initial velocity if a = 2, v = 15 and t = 7.
b![]() Find the acceleration if v = 10, u = 6 and t = 3.
Find the acceleration if v = 10, u = 6 and t = 3.
c![]() Find the time if v = 20, u = 5 and a = 3.
Find the time if v = 20, u = 5 and a = 3.
Solution
| a | v | = u + at |
|
| When a = 2, v = 15 and t = 7, | |||
| 15 | = u + 2 × 7 | ||
| 15 | = u + 14 | ||
| u | = 1 | ||
| The initial velocity is 1 m/s. | |||
| b | v | = u + at | |
| When v = 10, u = 6 and t = 3. | |||
| 10 | = 6 + 3a | ||
| 4 | = 3a | ||
| a | =  |
||
The acceleration is  = m/s2. = m/s2. |
|||
| c | v | = u + at | |
| When v = 20, u = 5 and a = 3, | |||
| 20 | = 5 + 3t | ||
| 15 | = 3t | ||
| t | = 5 | ||
| The time is 5 seconds. | |||
In the above example the measurements are those from the International System of Units. The formula would not make sense if the velocity was entered in km/h and the time in seconds. Great care has to be taken with units. There are other sets of consistent units for this problem. For example, working with kilometres and hours and the corresponding derived units will give correct results.
In the example above substitution resulted in an equation to be solved.. Methods of solutions of linear equations were discussed in the module, Linear Equations.
In the following, different techniques are required to solve the resulting equation
EXAMPLE
The thin lens formula states that 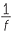 =
=  +
+  , where u cm is the distance from the object to the lens, v cm is the distance of the image from the lens and f cm is the focal length of the lens.
, where u cm is the distance from the object to the lens, v cm is the distance of the image from the lens and f cm is the focal length of the lens.
a![]() Find f if u = 2 and v = 5.
Find f if u = 2 and v = 5. ![]() b
b![]() Find u if f = 2 and v = 6.
Find u if f = 2 and v = 6.
Solution
| a | 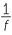 |
=  + +  |
|
| When u = 2 and v = 5, | |||
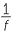 |
=  + + 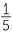 |
||
= 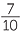 |
|||
Taking reciprocals of both sides of the equation gives f = 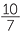 .
.
| b |  |
=  + +  |
|
| When f = 2 and v = 6, | |||
 |
=  + +  |
||
 |
=  − −  |
||
= 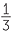 . . |
|||
Taking reciprocals of both sides of the equation gives u = 3.
EXAMPLE
The period T seconds of a simple pendulum is given by the formula
![]() T = 2π
T = 2π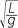
Where L metres is the length of the pendulum and g m/s2 is the acceleration due to gravity. Find L if T = 2.5. Take g = 9.8.
Solution
T = 2π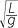
When T = 2.5 and g = 9.8,
2.5 = 2π
Square both sides of the equation.
| 6.25 | = 4π2 × 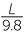 |
| L | = 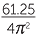 |
| ≈ 1.5514…… | |
| = 1.55 (correct to two decimal places) |
The length of the pendulum is 1.55 metres correct to the nearest centimetre.
Changing the subject of a formula
Sometimes the variable whose value is to be determined is not the subject of the formula. In this situation you have a choice. You can either:
- Rearrange the formula to make another variable whose value is to be determined the subject and then substitute (Method 1), or
- Substitute the values for the known variables and then solve the resulting equation for the unknown variable (Method 2).
In either case, an equation has to be solved. In Method 2, the equation involves numbers. In Method 1, the equation involves variables. We have used Method 2 in the previous section.
It is preferable to use Method 1, particularly, when you are asked to find several values of a variable that is not the subject of the formula. Changing the subject of a formula is an important skill.
EXAMPLE
The cost $C of hiring Scott’s car for one day is given by the formula C =  x + 40, where x is the number of kilometres driven. Find the number of kilometres driven by a customer who is charged $130 for hiring the car.
x + 40, where x is the number of kilometres driven. Find the number of kilometres driven by a customer who is charged $130 for hiring the car.
Solution
Method 1
Rearrange the formula to make x the subject and then substitute the given value of C,
as follows.
| C | =  x + 40 x + 40 |
|||
| C − 40 | =  x x |
(Subtract 40 from both sides.) | ||
| x | = 4C − 160 | (Multiply both sides by 4.) | ||
| When C = 130, x = 4 × 130 − 160 | ||||
| = 360 | ||||
Thus the customer drove 360km.
Method 2
Substitute the numbers and then solve the resulting equation, giving
| C | =  x + 40. When C = 130, x + 40. When C = 130, |
|||
| 130 | =  x + 40 x + 40 |
|||
| 90 | =  x x |
(Subtract 40 from both sides.) | ||
| x | = 360 | (Multiply both sides by 4.) | ||
Thus the customer drove 360km.
EXAMPLE
Given the formula v2 = u2 + 2as:
a![]() Rearrange the formula to make s the subject.
Rearrange the formula to make s the subject.
b![]() Find the value of x when u = 4, v = 10 and a = 2.
Find the value of x when u = 4, v = 10 and a = 2.
Solution
| a | v2 | = u2 + 2as | |||
| v2 − u2 | = 2as | (Subtract u2 from both sides of the formula.) | |||
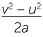 |
= s | (Divide both sides of the equation by 2a.) |
| b | When u = 4, v = 10 and a = 2 | ||
| x | = 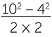 |
||
| = 21 | |||
Formulas are central to the study of mathematics and science. They are a part of virtually every topic in senior secondary mathematics.
The formulas for motion in a straight line with constant acceleration have been used in the Content section. They are an example of a very useful application of formulas.
The Ancient Egyptians undertook the development of mathematical recipes (formulas). In the Ahmose (Rhind) papyrus (c.1650 BC) there are several problems involving measurement. In the problems involving finding the area of circle it is assumed that the reader knows that the area of the circle is the area of the square whose side is obtained by removing 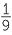 of the diameter. In modern algebraic notation this gives that the area A of the circle is given by
of the diameter. In modern algebraic notation this gives that the area A of the circle is given by
A = 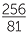 r2.
r2.
From the Moscow papyrus (c. 1850 BC) there are procedures for finding the volume of a cylindrical silo and for finding the volume of a frustum formed by truncating a square pyramid.
The Greek certainly had methods for estimating the area of a circle and this is discussed both in Euclid’s Elements and in the work of Archimedes.
Euclid in Book XII discusses the calculation of volumes and stated that ‘the pyramid has one third of the volume of the prism on the same base’ and gave several other results.
Archimedes described the relationship between the volumes of related solids, including the sphere and the inscribed cone. He understood the role of the number that we now call π and proved that 3.14084507042 < π < 3.14285714286.
Algebraic notation as we know it today did not appear until the middle of the 17th century. Many of the scientific discoveries of the 17th − 20th centuries resulted in formulas. Scientists such as Newton, Ampere, Maxwell, Ohm, Boyle and many others expressed their ideas through mathematical formulas.
Many mathematicians and scientists of the 17th to 19th century embraced the philosophy of determinism. Formulas were central to scientific and mathematical research. Their belief in the power and certainty provided by science and mathematics is illustrated by the following quote of the famous mathematician, Laplace.
‘We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at any given moment knew all of the forces that animate nature and the mutual positions of the beings that compose it, if this intellect were vast enough to submit the data to analysis, could condense into a single formula the movement of the greatest bodies of the universe and that of the lightest atom; for such an intellect nothing could be uncertain and the future just like the past would be present before its eyes.’
— Marquis Pierre Simon de Laplace (1749 −1827)
Modern Physics no longer believes this in the naive form that Laplace has stated it.
Formulas are used in many different areas. We have given several examples of formulas that are used in science.
Here are several examples from disparate sources:
- The formula (recipe) to estimate the weight of a horse - the units involved are kilograms and centimetres
Body weight = 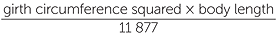
- Basal metabolic rate (BMR) is the amount of daily energy expended while at rest.
One set of formulas is given here.
Women: BMR = 655 + (9.6 × weight in kilos ) + (1.8 × height in cm ) − (4.7 × age in years)
Men: BMR = 66 + (13.7 x weight in kilos) + (5 x height in cm) − (6.8 x age in years )
Energy is given in kilocalories.
- An estimate of the percentage of games won in a baseball competition. The following formula gives good results
Estimate of percentage of games won = 
| A = πr2 | Area of a circle | |
| A = lw | Area of a rectangle | |
| A = bh | Area of a triangle | |
| A = bh | Area of a parallelogram | |
| A = (a + b) | Area of a trapezium | |
A = 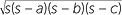 |
Heron’s formula for the area of a triangle where | |
s = 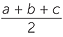 |
| A = 2πrh | Curved surface area of a cylinder | |
| A = 4πr2 | Surface area of a sphere | |
| A = 2πrl | Surface area of the curved surface of a cone |
| V = lwh | Volume of a rectangular prism | |
| V = x3 | Volume of a cube | |
| V = Ah | Volume of a prism | |
| V = πr2h | Volume of a cylinder | |
V =  πr3 πr3 |
Volume of a sphere | |
V = 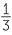 πr2h πr2h |
Volume of a cone |
Common formulas from Physics
Motion in a straight line with constant acceleration
| s= vt | Constant velocity | |
| v = u + at | Constant acceleration a, initial velocity u, velocity v at time t | |
| s = ut + at2 | Constant acceleration a, initial velocity u, position s at time t | |
| v2 = u2 + 2as | Constant acceleration a, initial velocity u, position s at time t, velocity v at time t |
|
s = 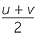 t t |
Constant acceleration a, initial velocity u, velocity v at time t |
= 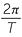 |
angular rate , T is the period for one rotation | |
| v = r | r is the radius of the circle, v the speed of the object | |
| a = 2r | inward acceleration a |
| F = ma | A body of mass m subjected to an acceleration F has an acceleration | |
EK =  mv2 mv2 |
Kinetic energy | |
| U = mgh | Potential Energy | |
F = G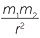 |
Gravitational force |
Electricity, Electrostatics and Magnetism
F = ke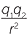 |
Electrostatic force | |
 = C = C |
Capacitance | |
 = =  + +  |
Capacitors in series | |
R = 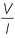 |
Ohm’s Law | |
 = =  + +  |
Resistors in parallel |
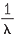 = RZ2 = RZ2 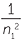 − − 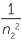  |
Rydberg formula for wave length | |
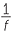 = =  + +  |
Lens formula |
F = 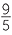 C + 32 C + 32 |
Centigrade to Fahrenheit conversion | |
| I = Prt | Simple interest | |
| A = P(1 + R)n | Compound interest | |
| A = P(1 − R)n | Compound depreciation |
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

