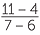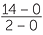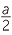The Improving Mathematics Education in Schools (TIMES) Project
Introduction to Coordinate Geometry
Number and Algebra : Module 29![]() Years : 9-10
Years : 9-10
June 2011
- Fluency with the arithmetic of the rational numbers
- Knowledge of ratios
- Congruent and similar triangles
- Basic algebraic notation
- Fluency with algebraic expressions and equations
- Basic plotting points in the Cartesian plane including plotting points from a table of values.
Coordinate geometry is one of the most important and exciting ideas of mathematics. In particular it is central to the mathematics students meet at school. It provides a connection between algebra and geometry through graphs of lines and curves. This enables geometric problems to be solved algebraically and provides geometric insights into algebra.
The invention of calculus was an extremely important development in mathematics that enabled mathematicians and physicists to model the real world in ways that was previously impossible. It brought together nearly all of algebra and geometry using the coordinate plane. The invention of calculus depended on the development of coordinate geometry.
It is expected that students have met plotting points on the plane and have plotted points from tables of values of both linear and non linear functions.
The number plane (Cartesian plane) is divided into four quadrants by two perpendicular axes called the x-axis (horizontal line) and the y-axis (vertical line). These axes intersect at a point called the origin. The position of any point in the plane can be represented by an ordered pair of numbers (x, y). These ordered pairs are called the coordinates of the point.
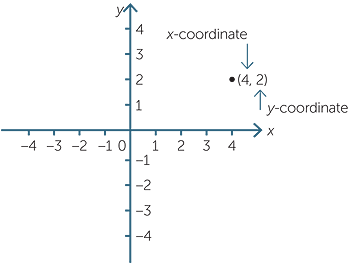 The point with coordinates (4, 2) has been plotted on the Cartesian plane shown. The coordinates of the origin are (0, 0).
The point with coordinates (4, 2) has been plotted on the Cartesian plane shown. The coordinates of the origin are (0, 0).
Once the coordinates of two points are known the distance between the two points and midpoint of the interval joining the points can be found.
Distances are always positive, or zero if the points coincide. The distance from A to B is the same as the distance from B to A. We first find the distance between two points that are either vertically or horizontally aligned.
EXAMPLE
Find the distance between the following pairs of points.
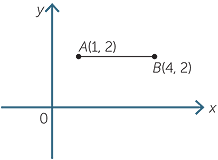
a![]() A(1, 2) and B(4, 2)
A(1, 2) and B(4, 2)![]() b
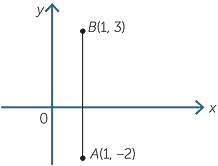
b![]() A(1, −2) and B(1, 3)
A(1, −2) and B(1, 3)
Solution
 a
a![]() The distance AB = 4 − 1 = 3
The distance AB = 4 − 1 = 3
Note: The distance AB is obtained from
the difference of the x-coordinates of
the two points.
 b
b![]() The distance AB = 3 − (−2) = 5
The distance AB = 3 − (−2) = 5
Note: The distance AB is obtained from
the difference of the y-coordinates of the
two points.
The example above considered the special cases when the line interval AB is either horizontal or vertical. Pythagoras’ theorem is used to calculate the distance between two points when the line interval between them is neither vertical nor horizontal.
The distance between the points A(1, 2) and B(4, 6) is calculated below.
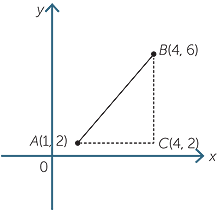
AC = 4 − 1 = 3 and BC = 6 − 2 = 4.
By Pythagoras’ theorem,
![]() AB2 = 32 + 42 = 25
AB2 = 32 + 42 = 25
And so ![]() AB = 5
AB = 5
The general case
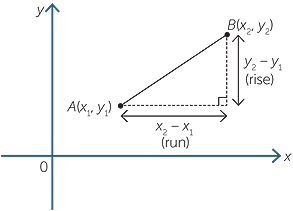
We can obtain a formula for the length of any interval. Suppose that P(x1, y1) and Q(x2, y2) are two points.
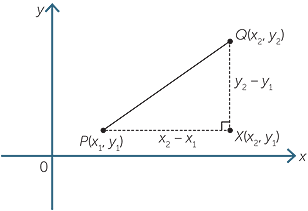
Form the right-angled triangle PQX, where X is the point (x2, y1),
![]() PX = x2 − x1 or x1 − x2 and
PX = x2 − x1 or x1 − x2 and![]() QX = y2 − y1 or y1 − y2
QX = y2 − y1 or y1 − y2
depending on the positions of P and Q.
By Pythagoras’ theorem:
![]() PQ2 = PX2 + QX2
PQ2 = PX2 + QX2
![]() = (x2 − x1)2 + (y2 − y1)2
= (x2 − x1)2 + (y2 − y1)2
Therefore ![]() PQ = QP =
PQ = QP = 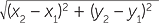
Note that (x2 − x1)2 is the same as (x1 − x1)2 and therefore it doesn’t matter whether we go from P to Q or from Q to P − the result is the same.
EXAMPLE
Find the distance between the points A(−4, −3) and B(5, 7).
Solution
In this case, x1 = −4, x2 = 5, y1 = −3 and y2 = 7.
AB2 = (x2 − x1)2 + (y2 − y1)2
![]() = (5 − (−4))2 + (7 − (−3))2
= (5 − (−4))2 + (7 − (−3))2
![]() = 92 + 102
= 92 + 102
![]() = 181
= 181
Thus, AB = 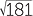
Note that we could have chosen x1 = 5, x2 = −4, y1 = 7 and y2 = −3 and still obtained the same result. As long as (x1, y1) refers to one point and (x2, y2) the other point, it does not matter which one is which.
EXERCISE 1
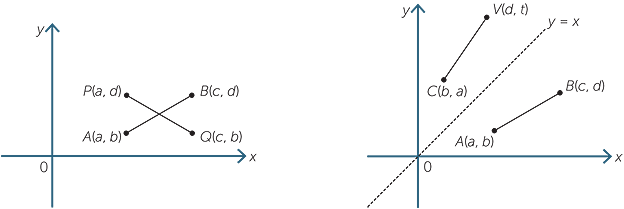
Show that the distance between the points A(a, b) and B(c, d) is the same as the
distance between
- the points P(a, d) and Q(c, b)
- the points U(b, a) and V(d, c)
Illustrate both of these.
EXERCISE 2
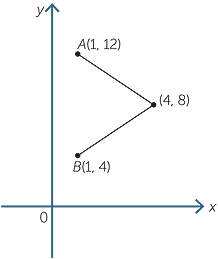
The distance between the points (1, a) and (4, 8) is 5. Find the possible values of a and use a diagram to illustrate.
The coordinates of the midpoint of a line interval can be found using averages as we will see.
We first deal with the situation where the points are horizontally or vertically aligned.
EXAMPLE
Find the coordinates of the midpoint of the line interval AB, given:
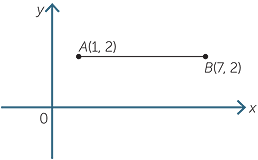
a![]() A(1, 2) and B(7, 2)
A(1, 2) and B(7, 2) ![]() b
b![]() A(1, −2) and B(1, 3)
A(1, −2) and B(1, 3)
Solution
 a
a![]() AB is a horizontal line interval, the
AB is a horizontal line interval, the
midpoint is at (4, 2), since 4 is halfway
between 1 and 7.
Note: 4 is the average of 1 and 7, that is, 4 = 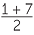 .
.
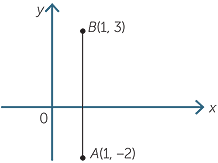
b![]() The midpoint of AB has coordinates 1,
The midpoint of AB has coordinates 1,  .
.
![]() Note that
Note that  is the average of 3 and −2.
is the average of 3 and −2.
When the interval is not parallel to one of the axes we take the average of the x-coordinate and the y-coordinate. This is proved below.
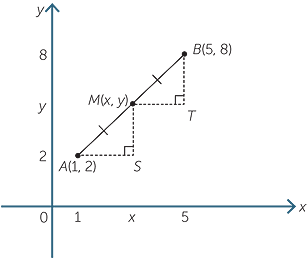
Let M be the midpoint of the line AB. Triangles AMS and MBT are congruent triangles (AAS), and so AS = MT and MS = BT.
Hence the x-coordinate of M is the average of 1 and 5.
![]() x =
x = 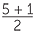 = 3
= 3
The y coordinate of M is the average of 2 and 8.
![]() x =
x = 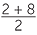 = 5
= 5
Thus the coordinates of the midpoint M are (3, 5).
The general case
We can find a formula for the midpoint of any interval. Suppose that P(x1, y1) and Q(x2, y2)are two points and let M(x, y) be the midpoint.
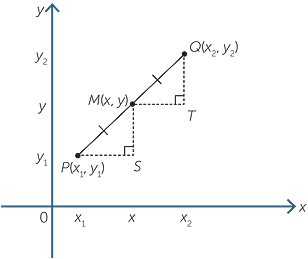
Triangles PMS and MQT are congruent triangles (AAS), and so PS = MT and MS = QT.
Hence the x-coordinate of M is the average of x1 and x2, and y-coordinate of M is the average of y1 and y2. Therefore
![]() x =
x = 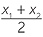 and y =
and y = 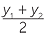
Midpoint of an interval
The midpoint of an interval with endpoints P(x1, y1) and Q(x2, y2) is 
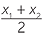 ,
,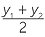
 .
.
Take the average of the x-coordinates and the average of the y-coordinates.
EXAMPLE
Find the coordinates of the midpoint of the line interval joining the points (6, 8) and (−3, 2).
Solution
The midpoint has coordinates, 
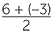 ,
, 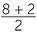
 =
= 
 , 5
, 5
EXAMPLE
If C(3, 6) is the midpoint of line interval AB and A has coordinates (−1, 1), find the coordinates of B.
Solution
Let the coordinates of B be (x1, y1).
![]()
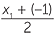 = 3 and
= 3 and 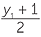 = 6
= 6
![]() x1 − 1 = 6
x1 − 1 = 6 ![]() y1 + 1 = 12
y1 + 1 = 12
so x1 = 7![]() so y1 = 11.
so y1 = 11.
Thus B has coordinates (7, 11).
EXERCISE 3
A square has vertices O(0, 0), A(a, 0), B(a, a) and C(0, a).
- a
- Find the midpoint of the diagonals OB and CA.
- b
- Find the length of a diagonal of the square and the radius of the circle in which OABC is inscribed.
- c
- Find the equation of the circle inscribing the square.
Gradient of an interval
The gradient is a measure of the steepness of line. There are several ways to measure steepness. In coordinate geometry the standard way to define the gradient of an interval AB is  where rise is the change in the y-values as you move from A to B and run is the change in the x-values as you move from A to B. We will usually the pronumeral m for gradient.
where rise is the change in the y-values as you move from A to B and run is the change in the x-values as you move from A to B. We will usually the pronumeral m for gradient.
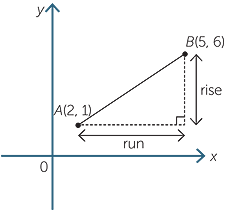
Given the points A(2, 1) and B(5, 6):
gradient of interval AB =  =
= 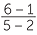 =
= 
Notice that as you move from A to B along the interval the y-value increases as the x-value increases. The gradient is positive.
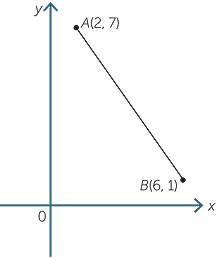 Given the points A(2, 7) and B(6, 1)
Given the points A(2, 7) and B(6, 1)
![]() gradient of interval AB =
gradient of interval AB =  =
= 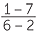 =
=  = −
= −
![]() or
or
![]() gradient of interval BA =
gradient of interval BA =  =
= 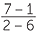 = −
= −
Notice that in this case as we move from A to B the y value decreases as the x value increases. The gradient is negative. Similarly the gradient of BA = − which is the same as the gradient of AB.
which is the same as the gradient of AB.
 In general:
In general:
![]() gradient of line interval AB =
gradient of line interval AB = 
![]() m =
m = 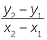
Note that since 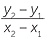 =
= 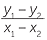 it does not
it does not
matter which point we take as the first and
which point we take as the second.
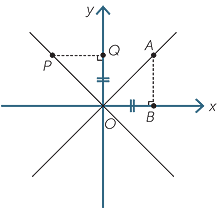
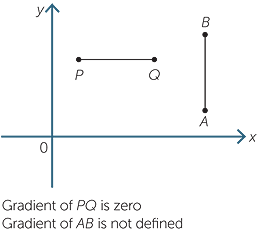 If the interval is vertical, the run is zero
If the interval is vertical, the run is zero
and the gradient of the interval is not
defined. This is shown by interval AB.
If the interval is horizontal, the rise is zero
as shown by interval PQ. The gradient of
the interval is zero.
Gradient of a line
The gradient of a line is defined to be the gradient of any interval within the line.
This definition depends on the fact that two intervals on a line have the same gradient.
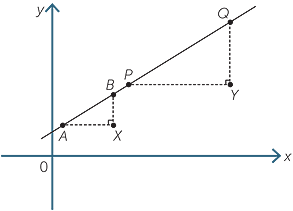
Suppose AB and PQ are two intervals on the same straight line. Draw right-angled triangles ABX and PQY with sides AX and PY parallel to the x-axis and sides BX and QY parallel to the y-axis.
Triangle ABX is similar to triangle PQY since the corresponding angles are equal. Therefore:
![]()
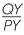 =
= 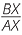
That is, the intervals have the same gradient.
EXAMPLE
A line passes through the points (1, 2) and (5, 10). Find its gradient.
Solution
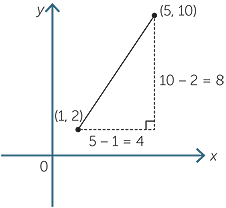
![]() gradient =
gradient = 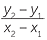
![]() =
= 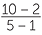
![]() = 2
= 2
EXAMPLE
A line passes through the point (5, 7) and has gradient 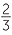 . Find the x-coordinate of a point on the line when y = 13.
. Find the x-coordinate of a point on the line when y = 13.
Solution
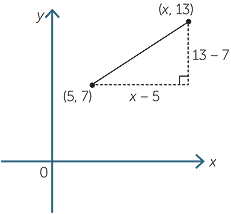 Gradient of the line =
Gradient of the line = 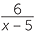 . Thus,
. Thus,
![]()
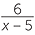 =
= 
![]() 18 = 2(x − 5)
18 = 2(x − 5)
![]() 9 = x − 5
9 = x − 5
![]() x = 14
x = 14
EXERCISE 4
Find the gradient of the line passing through (a, b) and (0, c)
Intercepts
The x-intercept of a line is the point at which it crosses the x-axis.
The y-intercept of a line is the point at which it crosses the y-axis.
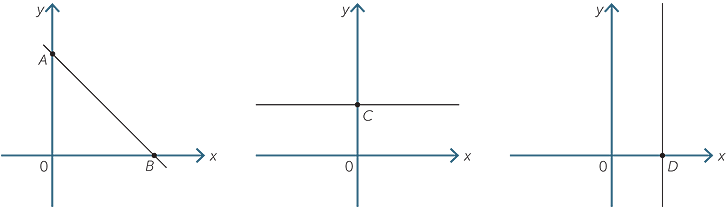
In the diagram to the left the y-intercept is at A and the x-intercept at B.
The second diagram shows a line parallel to the x-axis and it has a y-intercept at C.
The third diagram shows a line parallel to the y-axis and it has an x-intercept at D.
 When we plot points which satisfy the equation
When we plot points which satisfy the equation
y = 2x + 1 we find that they lie in a straight line.
Can we find the equation of the line given suitable geometric information about the line? The following shows that this can be done given the gradient of the line and the y-intercept.
Consider the line with gradient 3 and y-intercept 2. This passes through the point A(0, 2). Let B(x, y) be any point on this line.
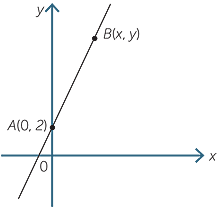
| Gradient of interval AB | =  |
|
= 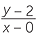 |
||
= 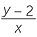 |
The gradient of the line is 3.
| So, | 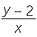 |
= 3 |
| Rearranging | y − 2 | = 3x |
| y | = 3x + 2 |
So the coordinates of B(x, y) satisfies y = 3x + 2. This is called the equation of the line.
Conversely suppose that B(x, y) satisfies the equation y = 3x + 2, then 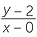 = 3 and it passes the point (0, 2) so the point lies on the line with gradient 3 and y-intercept 2.
= 3 and it passes the point (0, 2) so the point lies on the line with gradient 3 and y-intercept 2.
We summarise this by saying that the equation of the line is y = 3x + 2.
Consider the line with gradient m and y-intercept c. If passes through the point A(0, c).
Let B(x, y) be any point on this line.
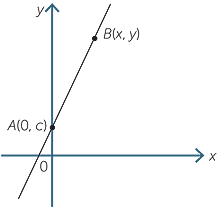
| Gradient of interval AB | =  |
|
= 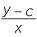 |
We know the gradient of the line is m.
| Therefore | 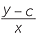 |
= m | |
| y − c | = mx | ||
| y | = mx + c |
That is, the line in the cartesian plane with gradient m and y-intercept c has equation
y = mx + c. Conversely, the points whose coordinates satisfy the equation y = mx + c always lie on the line with gradient m and y-intercept c.
Vertical and horizontal lines
Vertical lines
In a vertical line all points have the same x-coordinate, but the y-coordinate can take any value. The equation of the vertical line through the point (6, 0) is x = 6. The x-axis intercept is 6. All the points on this line have x-coordinate 6.
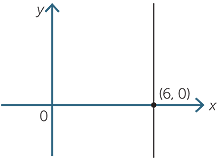
In general, the equation of the vertical line through P(a, b) is x = a.
Because this line does not have a gradient it cannot be written in the form
![]() y = mx + b.
y = mx + b.
Horizontal lines
A horizontal line has gradient 0. In a horizontal line all points have the same y-coordinate, but the x-coordinate can take any value. The equation of the horizontal line through the point (0, 5) is y = 5. The equation of the horizontal line through the point (9, 5) is y = 5.
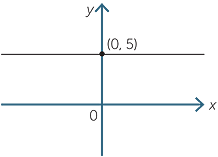
In general, the equation of the horizontal line through P(a, b) is y = b.
EXAMPLE
Write down the gradient and y-intercept of the line with equation y = 3x − 4.
Solution
The gradient of the line is 3 and the y-intercept is −4.
Sometimes an equation needs to be rearranged before the gradient and y-intercept can be determined. Consider the following example.
EXAMPLE
Rewrite the equation 2x + 3y = 6 in the form y = mx + c and hence find the value of the gradient and y-intercept.
Solution
| 2x + | 3y | = 6 | |
| so | 3y | = 6 − 2x | |
| that is, | y | = 2 −  |
|
| Thus | y | = − + 2 + 2 |
The gradient of the line is −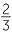 and the y-intercept is 2.
and the y-intercept is 2.
Equation of a line given its gradient and a point on the line
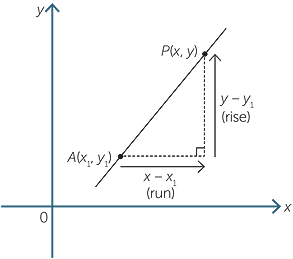 We want to find the equation of the line
We want to find the equation of the line
with gradient m and which passes through
the point P(x1, y1).
Let P(x, y) be any point with x ≠ x1 on the line
passing through the point A(x1, y1) and let m
be the gradient of this line.
| Using gradient, | m = 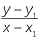 |
| and | y − y1 = m(x − x1) |
This is the equation of the straight line with gradient m passing through the point A(x1, y1).
EXAMPLE
Find the equation of the line that passes through the point (−2, 3) with gradient −4.
Solution
The equation for this line is:
| y − y1 | = m(x − x1) | |
| y − 3 | = −4(x − (−2)) |
| that is, | y − 3 | = −4x − 8 |
| y | = −4x − 5 |
Note that it is usual to give the answer in the form y = mx + c
Equation of a straight line given two points
Given two points A(x1, y1) and B(x2, y2) the equation of the line passing through the two points can be found.
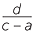
The gradient m of the line passing through A(x1, y1) and B(x2, y2) = 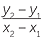 , x2 ≠ x1
, x2 ≠ x1
Substituting into y − y1 = m(x − x1) gives
y − y1 = 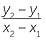 (x − x1) , x2 ≠ x1
(x − x1) , x2 ≠ x1
Using the equation to sketch the line
If you are given an equation of a straight line and asked to draw its graph all you need to do is find two points whose coordinates satisfy the equation and plot the points. There are two commonly used methods to find two points.
Using the y-intercept and one other point
Using the y-intercept and a second point the equation can be found .
EXAMPLE
Draw the graph of y = 2x + 3.
Solution
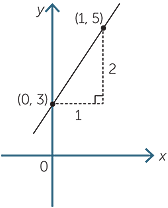 The y-intercept is 3 and the gradient 2.
The y-intercept is 3 and the gradient 2.
Substitute x = 1, so y = 5 giving the point (1, 5)
lies on the line.
Plot the two points and draw the line through them.
This method does not work if the line is parallel to the y-axis.
EXAMPLE
The gradient of a line is −6 and the y-intercept is 2. Find the equation of the line and sketch it.
Solution
Using the y = mx + c form for the equation of a straight line.
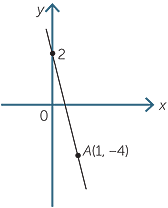 The equation of the line is y = −6x + 2.
The equation of the line is y = −6x + 2.
The point (0, 2) lies on the line.
| Substitute x = 1 in y | = −6x + 2 |
| = −6 × 1 + 2 | |
| = −4 |
The point (1, −4) lies on the line. The graph is shown.
x-intercept y-intercept method
In this method both intercepts are found.
- The x-intercept is found by substituting y = 0 and
- The y-intercept is found by substituting x = 0.
This method does not work if the line is parallel to an axis or passes through the origin.
EXAMPLE
Using the x-intercept y-intercept method sketch the graph of:
| a | y = 3x − 4 | b | 2x + 3y + 6 = 0 |
Solution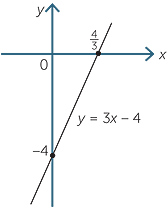
| a | When x = 0, | y = −4 | |
| When y = 0, | 3x − 4 | = 0 | |
| 3x | = 4 | ||
| x | =  |
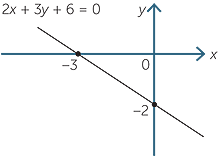
| b | When x = 0, | 3y + 6 | = | 0 |
| 3y | = | −6 | ||
| y | = | −2 | ||
| When y = 0, | 2x + 6 | = | 0 | |
| 2x | = | −6 | ||
| x | = | −3 |
The general form for the equation of a straight line
The equations y = 2x − 3, x = 6 and 2x − 3y = 6 can be written as −2x + y + 3, x − 6 = 0 and 2x − 3y − 6 = 0 respectively.
The general form for the equation of a line is ax + by + c = 0 where a, b and c are constants and a ≠ 0 or b ≠ 0. The equation of every line can be put in general form. The general form is not unique. The equation x + 2y +1 = 0 is the same straight line as
2x + 4y + 2 = 0.
EXERCISE 5
An equilateral triangle ABC has coordinates O(0, 0), B(a, 0) and C(c, d).
a Find c and d in terms of a by using the fact that OB = BC = CO.
b Find the equation of the lines OB, BC and CO.
Parallel and perpendicular lines
Parallel lines
If two lines l1 and l2 are parallel then corresponding angles are equal.
Conversely, if corresponding angles are equal then the lines are parallel.
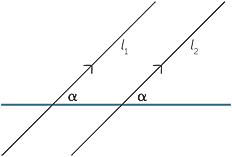
Theorem
Two lines are parallel if they have the same gradient and conversely,
two lines with the same gradient are parallel.
Proof
In the diagram, two lines are drawn and the right-angled triangles PQX and ABY are added with QX = BY.
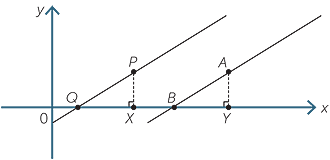
If the lines are parallel then ![]() PQX =
PQX = ![]() ABY (corresponding angles).
ABY (corresponding angles).
The two triangles are congruent by the AAS test.
Therefore PX = PY and 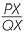 =
= 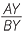 .
.
That is, the gradients are equal.
Conversely. If the gradients are equal 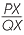 =
= 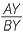 .
.
Now QX = BY and therefore PX = AY.
Hence the triangles QPX and ABY are congruent by the SAS test.
Hence the corresponding angles PQX and ABY are equal and the lines are parallel.
EXAMPLE
Show that the line passing through the points A(6, 4) and B(7, 11) is parallel to the line passing through P(0, 0) and Q(2, 14).
Solution
|
Gradient of AB = |
|
Gradient of PQ = |
The two lines have the same gradient and so are parallel.
EXAMPLE
Find the equation of the line that is parallel to the line y = −2x + 6 and passing through the point A(1, 10).
Solution
The gradient of the line y = −2x + 6 is −2.
Therefore the line through the point A(1, 10) parallel to y = −2x + 6 has equation:
| y − y1 = m(x − x1) | |
| y − 10 = −2(x − 1) | |
| y = −2x + 12 |
Perpendicular lines
When we draw y = 3x and draw a line perpendicular to it passing through the origin then it is clear that y = −ax where a is a small positive number. We will show that the equation is y = −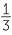 x.
x.
We are now going to show the surprising result that ‘if two lines are perpendicular then the product of their gradients is −1’ (or if one is vertical and the other horizontal). The converse is also true. That is, ‘ If the product of the gradients of two lines is −1 then they are perpendicular’.
We first consider the case when both lines pass through the origin.
Draw two lines passing through the origin with one of the lines having positive gradient and the other negative gradient.
Form right-angled triangles OPQ and OAB with OQ = OB.
| Gradient of the line OA | = | 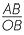 |
|
| Gradient of the line through OP | = | −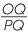 |
|
| The product | = | −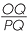 × × 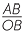 |
|
| = | −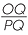 × × 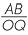 |
(since OQ = OB) | |
| = | −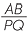 |
If the lines are perpendicular, ![]() POQ =
POQ = ![]() AOB.
AOB.
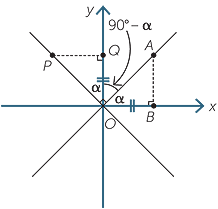
Therefore  OPQ
OPQ 
 OAB (AAS),
OAB (AAS),
so PQ = AB and the product, −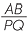 , of the gradients is −1.
, of the gradients is −1.
Conversely If the product is −1, then AB = PQ,
so  OAB
OAB 
 OPQ (SAS).
OPQ (SAS).
Therefore ![]() POQ =
POQ = ![]() AOB and so
AOB and so ![]() AOP = 90°.
AOP = 90°.
We have now proved the result for lines through the origin.
If we are given two lines anywhere in the plane, we can draw lines through the origin parallel to the given two lines. The gradient of each new line is the same as the gradient of the corresponding original line. So the result holds for lines that do not necessarily pass through the origin.
EXAMPLE
Show that the line through the points A(6, 0) and B(0, 12) is perpendicular to the line through P(8, 10) and Q(4, 8).
Solution
| Gradient of AB | = 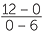 |
| = −2 | |
| Gradient of PQ | = 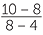 |
=  |
|
=  |
| (Gradient of AB) × (gradient of PQ) | = −2 ×  |
| = −1 |
Hence the lines are perpendicular.
Parallel and perpendicular lines
- If two non-vertical lines are parallel then they have the same gradient.
Conversely if two non-vertical lines have the same gradient then they are parallel. - If two non-vertical lines are perpendicular then the product of their gradients is −1. Conversely if the product of the gradients of two lines is −1 then they are perpendicular.
EXAMPLE
Find the equation of the line which passes through the point (1, 3) and is perpendicular to the line whose equation is y = 2x + 1.
Solution
Gradient of the line y = 2x + 1 is 2.
Gradient of a line perpendicular to this line is − .
.
| The required equation is y − 3 | = | − (x − 1) (x − 1) |
| 2(y − 3) | = | −(x − 1) |
| 2y + x | = | 7 |
Thus the equation of the required line is 2y + x = 7.
Proofs with coordinate geometry
Coordinate geometry can be used to prove results in Euclidean Geometry. An important aspect of doing this is placing objects on the Cartesian plane in a way that minimises calculations.
EXAMPLE
Prove that the midpoints of a parallelogram bisect each other using coordinate geometry.
Solution
Let the coordinates of the vertices be O(0, 0), A(a, 0), B(a + c, d) and C(c, d).
There is no loss in generality in placing the vertices of the parallelogram on the Cartesian plane in this way.
| The midpoint M of OB | = |  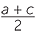 , , 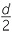  |
| The midpoint N of AC | = |  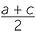 , , 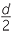  |
M = N and so the midpoints coincided which means that the diagonals bisect each other.
EXAMPLE
Prove that the diagonals of a rhombus bisect each other at right angles using coordinate geometry.
Solution
Let the coordinates of the vertices be O(0, 0), A(a, 0), B(a + c, d) and C(c, d).
Because it is a rhombus all the sides are of equal length.
| OA = AB = BC = CO | ||
| Gradient of OB | =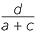 and, and, |
|
| Gradient of AC | =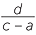 |
|
The product of the gradients of the diagonals = 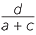 ×
× 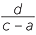 =
=  .
.
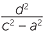
OA2 = a2 and by Pythagoras’ theorem, AB2 = c2 + d2
so a2 = c2 + d2.
Hence d2 = −(c2 − a2)
Thus the product of the gradients of the diagonals = −1.
EXERCISE 6
In any triangle ABC prove that AB2 + AC2 = 2(AD2 + DC2)
Where D is the midpoint of BC.
EXERCISE 7
Prove that set of points equidistant from two given points is a straight line.
EXERCISE 8
Prove that the lines joining the midpoints of opposite sides of a quadrilateral and the lines joining the midpoints of its diagonals meet in a point and bisect each other.
Coordinate geometry leads into many other topics in school mathematics. The techniques of coordinate geometry are used in calculus, functions, statistics and many other important areas.
There were three facets of the development of coordinate geometry.
- The invention of a system of coordinates
- The recognition of the correspondence between geometry and algebra
- The graphic representation of relations and functions
The Greek mathematician Menaechmus (380−320 BC) proved theorems by using a method that was very close to using coordinates and it has sometimes been maintained that he had introduced coordinate geometry.
Apollonius of Perga (262−190 BC) dealt with problems in a manner that may be called an coordinate geometry of one dimension; with the question of finding points on a line that were in a ratio to the others. The results and ideas of the ancient Greeks provided a motivation for the development of coordinate geometry.
Coordinate geometry has traditionally been attributed to René Descartes (1599−1650) and Pierre de Fermat (1601−1665) who independently provided the beginning of the subject as we know it today.
EXERCISE 1
AB2 = PQ2= UV2 = (d − b)2 + (c − a)2
EXERCISE 2
a = 4 or a = 12
EXERCISE 3
| a | 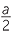 , , 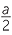 |
b | diagonal = 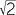 a, radius = a, radius = 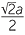 |
c |  x − x − 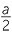  2 + 2 +  y − y − 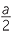  2 = 2 =  |
EXERCISE 4

EXERCISE 5
|
a |
c = |
b |
OA: y = 0, OC: y = |
EXERCISE 6
Place the triangle so D is at the origin. Then let the coordinates of B and C be (−a, 0) and (a, 0) respectively. Let the coordinates of A be (d, c).
| AB2 | = | c2 + (d + a)2 and AC2 = c2 + (d − a)2 | ||
| So | AB2 + AC2 | = | 2c2 + 2d2 + 2a2 | |
| AD2 | = | c2 + d2 and DC2 = a2 | ||
| Hence | AB2 + AC2 | = | 2(AD2 + DC2) |
EXERCISE 7
Let P(x, y) be a point equidistant from A(a, b) and C(c, d)
PA = PC
2(c − a)x + 2(d − b)y = d2 + c2 − a2 − b2
EXERCISE 8
Let the coordinates of the vertices be O(0, 0), A(a, c), B(m, n) and D(b, 0)
Show that the midpoint of all the required line segments has coordinates

 (m + b + a),
(m + b + a),  (n + c)
(n + c)
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()