The Improving Mathematics Education in Schools (TIMES) Project
- Fluency with addition, subtraction, multiplication and division of whole numbers
and fractions. - Familiarity with using a number line for whole numbers and fractions.
- Understanding place value for whole numbers.
- Students will have had some experience with decimals.
Decimals are used widely. Our money is based on a decimal system. Common measurements such as the height of students in a class, the price of petrol or the
amount of gas used for heating your home are usually expressed using decimals.
We can represent decimals as points on the number line by repeatedly subdividing intervals into tenths. A decimal number gives the ‘address’ of a point on the number line − the digits give successively more accurate information and together locate a point. This is an extension of the concept of place value met earlier. Whole numbers are written as strings of digits that correspond to the ‘places’ ones, ten, hundreds, etc. Positive numbers less than one can be written with the same notation with ‘additional places’ tenths, hundredths, thousandths, etc.
Despite their common use today, decimals were not used widely until the early seventeenth century. Now, decimals are used extensively and almost exclusively in commerce and science.
In mathematics, decimals can be used to represent both rational and irrational numbers. They are often used where measurements are taken and recorded to a given accuracy. Decimals lend themselves easily to approximations which can be given to any stated accuracy. Approximations will be discussed in the module,Introduction to Measurement.
Percentages are a way of writing numbers with denominator 100. For example
![]()
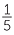 =
=  = 20%,
= 20%, 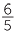 =
=  = 120% and
= 120% and 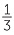 =
= 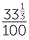 = 33
= 33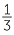 %.
%.
Percentages are used widely and in many different areas. For example bank interest rates, rates of inflation and many statistics in the media are often expressed as percentages. They are important for understanding the everyday aspects of the financial lives of people.
The word decimal comes from the Latin word decem, meaning ‘ten’. Decimal notation uses tenths, hundredths, thousandths, and so on, as well as units, tens, hundreds, thousands, and so on.
Decimals are a convenient and useful way of writing fractions with denominators
10, 100, 1000, etc:
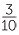 is written as 0.3,
is written as 0.3,  is written as 0.02,
is written as 0.02, 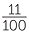 is written as 0.11 and
is written as 0.11 and  is written
is written
as 0.434
The number 25.24 is shorthand for
![]() 2 × 10 + 5 × 1 +
2 × 10 + 5 × 1 +  +
+  .
.
It should be observed that 25.24 can also be written as 25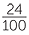 and read as
and read as
‘25 and 24 hundredths’.
The decimal point separates the units column from the tenths column. To the right of the decimal point, we read the names of the digits individually. For example, 125.2408 is read as ‘one hundred and twenty-five point two, four, zero, eight’.
Here is a chart illustrating place value in the decimal system.
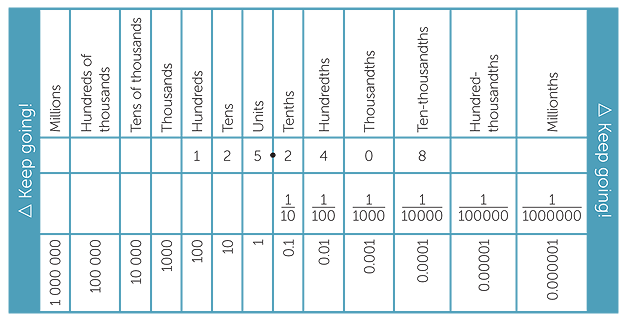
In decimals the number of places filled by the digits after (to the right of) the decimal point are called the decimal places. Thus, 345.607 has 3 decimal places and 0.2 has 1 decimal place.
Using the number line to compare decimals
On the number line 0.8 and 0.34 are both between 0 and 1. Because 0.8 is to the right of 0.34 we know that 0.8 > 0.34.
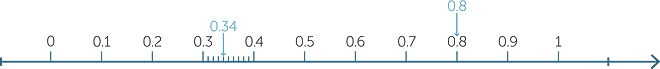
To make a decision about which of the numbers 4.2, 4.54 and 4.362 is largest we locate each number on the number line. We first focus on numbers between 4 and 4.6.
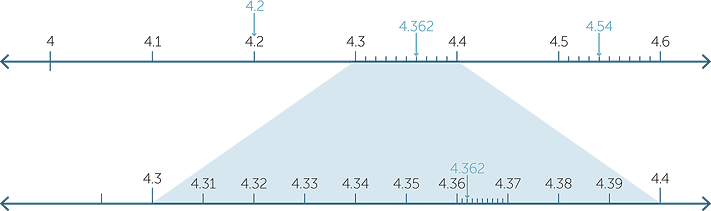
It is necessary to ‘zoom in’ on a section of the number line to show that 4.362 is between 4.36 and 4.37.
So we find that ![]() 4.2 < 4.362 < 4.54.
4.2 < 4.362 < 4.54.
Comparing numbers by working through the digits from left to right
One method for comparing decimals is to write the numbers one underneath the other, with the decimal points lined up.
For example, to compare 3.78 and 3.612, we first write the numbers one beneath the other, aligning the decimal points.
![]() 3.78
3.78
![]() 3.612
3.612
Next, we compare the whole-number parts. Both are the same, so we proceed to the next digit.
We compare the tenths: 7 tenths is larger than 6 tenths. So 3.78 is larger than 3.612.
Writing fractions in decimal notation and vice versa
Writing decimals as fractions and mixed numbers
To write 0.005 as a decimal, note that there are no tenths, no hundredths and five thousandths and thus we know 0.005 = 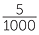 =
=  .
.
To write 2.36 as a mixed number, we write![]() 2.36 = 2
2.36 = 2 = 2
= 2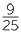
Writing fractions and mixed numbers as decimals
If we have a fraction where the denominator is a power of 10, it is easy to convert
it to a decimal. For example,
![]() 2
2 = 2.34.
= 2.34.
This can also be done as:
![]() 2
2 = 2 +
= 2 + 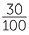 +
+  = 2.34.
= 2.34.
We first state that all positive numbers have a decimal representation.
Some fractions have a denominator which is a factor of a power of ten.
The following example shows how to write such a fraction as a decimal.
EXAMPLE
Convert 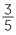 and
and  to decimals by finding an equivalent fraction with a denominator that is a power of 10.
to decimals by finding an equivalent fraction with a denominator that is a power of 10.
Solution
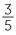 =
= 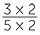 =
= 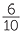 = 0.6
= 0.6![]()
![]()
 =
= 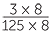 =
=  = 0.024
= 0.024
The division process
An alternative method is to divide the numerator of the fraction by its denominator as shown. The algorithm is an extension of the division algorithm.
EXAMPLE
Convert 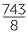 to a decimal using the division process.
to a decimal using the division process.
Solution
This can be done by several methods but the first step for each of these methods is to observe that
![]()
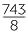 = 743 ÷ 8.
= 743 ÷ 8.
![]() The short division algorithm can be adapted.
The short division algorithm can be adapted.
![]() We set out 743 ÷ 8 as shown:
We set out 743 ÷ 8 as shown:
![]()
![]()
![]() We have had to add trailing zeros.
We have had to add trailing zeros.
The decimal 0.875 is a terminating decimal. The division process terminates.
By using a technique similar to that of the example above it can be shown that 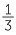 = 0.33333…. The digit 3 is obtained endlessly as new trailing zeros are added and
= 0.33333…. The digit 3 is obtained endlessly as new trailing zeros are added and
the division algorithm continued. The decimal 0.3333… is called a recurring decimal. These will be discussed later in this module.
There are many fractions whose decimal equivalent is not terminating.
The result of the following exercise determines which fractions are terminating decimals.
EXERCISE 1
A fraction (rational number) written in simplest form as 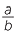 can be written as a terminating decimal if and only if the denominator b is a product of 2’s and 5’s only.
can be written as a terminating decimal if and only if the denominator b is a product of 2’s and 5’s only.
Determine which of the following fractions can be written as terminating decimals. Explain by giving the prime factorisation of the denominator.
| a |  |
b | 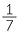 |
c | 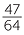 |
d | 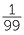 |
The algorithms for addition and subtraction of decimals are similar to those for
whole numbers.
Adding decimal numbers
We can always relate the addition of decimal numbers to addition of fractions.
Consider:
| 4.2 + 5.09 | = 4 + 5 + 5 |
=4 + 5 + 5 |
|
= 9 |
|
| = 9.29 |
However this is inefficient and the decimal notation gives us an easier way to calculate such sums.
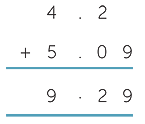
The decimal point in each number should be lined up one under the other.
The vertical addition algorithm is shorthand for adding hundreds to hundreds, tens to tens, ones to ones, tenths to tenths, and so on. It is important to line up the place value columns when lining up the decimal point.
Subtracting decimals
When subtracting one decimal from another, write the numbers one under the other as with whole number subtraction, making sure the decimal points are aligned.
Here are the two standard subtraction algorithms showing the methods used for subtracting 16.532 from 23.84.
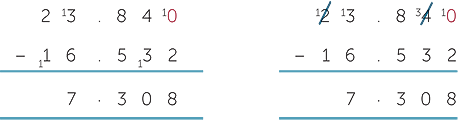
Sometimes, the number of decimal places is different in each of the numbers. It is helpful when doing subtractions that deal with these ‘ragged’ decimals to place additional zeroes at the end of the top number (in this case 23.84). This does not change the number; it simply says that there are ‘no thousandths’.
Multiplication and division by powers of 10
Multiplying
When any number is multiplied by a power of 10, each digit is multiplied by the same power of 10.
For example 24.06 × 10 = 20 × 10 + 4 × 10 + 0.06 × 10 = 200 + 40 + 0.6 = 240.6
- Multiplying by 10 corresponds to moving the decimal point one place to the right and inserting a zero where necessary.
- Similarly multiplying by 100 = 102 corresponds to moving the decimal point two places to the right and inserting zeros where necessary. For example: 8.7 × 100 = 870.
- Multiplying by 1000 = 103 corresponds to moving the decimal point three places to the right and inserting zeros where necessary. For example: 8.7 × 1000 = 8700.
Dividing
When any number is divided by a power of 10, each digit is divided by the same power of 10.
| 78.4 ÷ 100 | = 70 ÷ 100 + 8 ÷ 100 + 0.4 ÷ 100 | |
= 70 ×  + 8 × + 8 ×  + 0.4 × + 0.4 ×  |
||
| = 0.7 + 0. 08 + 0. 004 | ||
| = 0.784 |
- Dividing by 10 corresponds to moving the decimal point one place to the left and inserting a zero where necessary.
- Dividing by 100 = 102 corresponds to moving the decimal point two places to the left and inserting zeros if necessary.
- Dividing by 1000 = 103 corresponds to moving the decimal point three places to the left and inserting zeros if necessary.
A very common student error is to write
![]() 0.3 × 0.2 = 0.6.
0.3 × 0.2 = 0.6.
Clearly that is to be avoided and suggests that multiplying one decimal by another is best done by converting the decimals to fractions. The fractions can be multiplied in the usual way and converted back to decimals. For example,
| 0.6 × 0.4 | = | 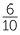 × ×  |
|
| = | 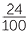 |
||
| = | 0.24 |
There is another commonly used method for multiplying decimals. Students seem to not carry out this method well. It was the pre-calculator method that was used widely.
The steps are as follows:
- Ignore the decimal points and multiply the factors as if they were whole numbers.
- Insert a decimal point in the product so that the total number of decimal places is the same on both sides of the equation.
For example,
![]() 2.5 × 0.06
2.5 × 0.06
Step 1: 25 × 6 = 150
Step 2: 2.5 × 0.06 = .150 = 0.15
This is discussed in the Appendix.
Division of decimals by whole numbers
If we had a piece of rope that was 4.8 metres long and wanted to cut it into 4 equal pieces we could cut it in two and then cut each piece in two again to get 4 pieces, each 1.2 metres in length. We can use the division algorithm to show this.
![]()
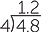
The procedure is the same as for whole numbers. The decimal point in the answer is aligned directly above the decimal point in the question.
We can relate this to division by fractions (invert and multiply)
| 4.8 ÷ 4 | =  ÷ ÷ 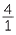 |
|
= 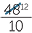 × ×  |
||
=  |
||
| = 1.2 |
If we were to divide a 4.8 metre piece of rope into 5 equal pieces, the procedure is a little more involved. We could divide 4.8 by 10 and double the result to get 0.96. This can be also be found using the division algorithm:
![]()
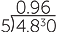
So, 4.8 cut into 5 equal lengths is 0.96. Each piece of the rope will be 0.96 metres
in length.
Now if we divide a 4.8 metre piece of rope into 7 equal pieces, the result cannot be expressed as a terminating decimal. This can be shown using division:
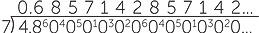
Thus the result of 4.8 ÷ 7 is 0.6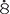 5714
5714 and is a recurring decimal where the block of digits which recurs is indicated by a dot over the first and last digits of the block. We will return to decimals of this form later in the module. It should be noted that in a practical situation you would probably want to know the length of each piece of rope to the nearest millimeter. Each piece of rope is to be 0.686 metres or 686 millimetres in length correct to the nearest millimetre.
and is a recurring decimal where the block of digits which recurs is indicated by a dot over the first and last digits of the block. We will return to decimals of this form later in the module. It should be noted that in a practical situation you would probably want to know the length of each piece of rope to the nearest millimeter. Each piece of rope is to be 0.686 metres or 686 millimetres in length correct to the nearest millimetre.
When the numbers are ‘nice’ it is possible to perform some divisions by decimal using common sense. For example
![]() 1.8 ÷ 0.3
1.8 ÷ 0.3
We can show what 1.8 ÷ 0.3 looks like on a number line using jumps of 0.3 until we get
to 1.8.

It takes 6 jumps of 0.3 to get to 0 from 1.8.
By multiplying each number by the same multiple of ten the division is easier to deal with.
![]() 1.8 ÷ 0.3 =
1.8 ÷ 0.3 = 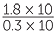 =
= 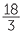 = 6
= 6
This suggests that we multiply both numbers by the same power of 10 to make the divisor a whole number and then use the division algorithm.
![]() 1.355 ÷ 0.05 = 135.5 ÷ 5
1.355 ÷ 0.05 = 135.5 ÷ 5
![]()
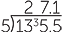
Alternatively we can relate division of decimals to division of fractions by writing each decimal as a fraction and completing the division.
| |
0.6 ÷ 0.4 | = | 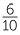 ÷ ÷  |
| = | 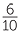 × × 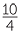 |
||
| = | 1.5 |
Earlier in this module we showed how to express fractions, whose denominator can be factorised as products of 2’s and 5’s, as a decimal. These decimals are terminating.
We now look at fractions whose denominator cannot be factored as a product of 2’s and 5’s. These produce recurring decimals; that is decimals with eventually repeating digits. We have met these previously in our discussion of division. (Obviously 3.0000… is not considered to be a recurring decimal.)
Numbers, such as 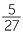 when written as a decimal, result in a block of digits that
when written as a decimal, result in a block of digits that
repeats indefinitely.
![]()
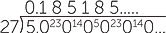
![]()
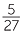 = 0.185185185… = 0.
= 0.185185185… = 0. 8
8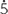
This is a recurring decimal and the dots above the 1 and the 5 digit indicate that 185 are the recurring digits. Some people prefer to write ![]() . where the bar indicates that 185 are the recurring digits.
. where the bar indicates that 185 are the recurring digits.
The fraction 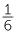 = 0.16666… = 0.1
= 0.16666… = 0.1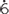 is an eventually recurring decimal but decimals with this property are still called recurring decimals.
is an eventually recurring decimal but decimals with this property are still called recurring decimals.
EXAMPLE
Convert 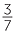 to a decimal.
to a decimal.
Solution
To convert 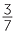 to a decimal divide 3 by 7. There is no multiple of 7 that is a power of 10.
to a decimal divide 3 by 7. There is no multiple of 7 that is a power of 10.
![]()
![]()
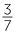 = 0.
= 0.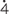 28 57
28 57
Theorem
We prove that every rational number, 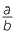 can be written as a terminating or recurring decimal. The above examples serve as illustrations of the proof.
can be written as a terminating or recurring decimal. The above examples serve as illustrations of the proof.
Proof
At each step of the division of a by b there is a remainder. If the remainder is 0 then the division algorithm stops and the decimal is a terminating decimal.
If the remainder is not 0, then it must be one of the numbers 1, 2, 3,…, b − 1. (In the above example, b = 7 and the remainders can only be 1, 2, 3, 4, 5 and 6.). Hence the remainder must repeat after at most b − 1 steps.
Note that calculators can only handle terminating decimals.
EXAMPLE
Find 4.543 ÷ 0.6
Solution
Multiply each number by 10 to get a divisor that is a whole number.
4.543 ÷ 0.6 becomes 45.43 ÷ 6
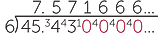
4.543 ÷ 0.6 = 7.571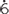
EXERCISE 2
Express each of the following as a recurring decimal.
| a | 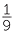 |
b |  |
c | 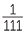 |
d | 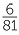 |
We meet and use percentage in many aspects of our lives. The word percent comes from the Latin per centum meaning ‘for each hundred’. Percentages will be central in several other modules. In this module their relationship with fraction and decimal notation is emphasised.
The symbol for percent is %. Percentage is another way to write fractions with a denominator of 100. For example,
8% =  |
25% =  |
99% =  |
150% = 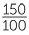 |
To understand percentages we need go no further than remembering that percent means ‘out of one hundred’.
A square that has been cut into 100 smaller squares can be used to model percentages.
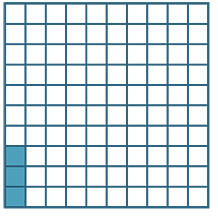 If we colour three of them, we say that ‘3 out of
If we colour three of them, we say that ‘3 out of
a hundred’ or ‘3 percent’ are coloured in.
We can write  = 3%.
= 3%.
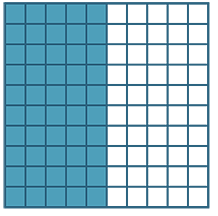 If we colour 50 of them we say that ‘50 out of
If we colour 50 of them we say that ‘50 out of
a hundred’ or ‘50 percent’ are coloured.
We can write = 50%. This is equivalent to 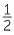 .
.
Writing percentages as fractions and decimals
Percentages are fractions with a denominator of 100. To convert a ‘whole number’ percentage to its fraction equivalent, write it as a fraction with a denominator of 100 and then simplify.
For example,
65% = 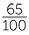 = =  |
150% = 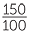 = 1 = 1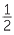 . . |
‘Whole number’ percentages can easily be written as decimals by writing them as fractions with a denominator of 100 and converting to a decimal. For example,
65% = 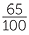 = 0.65 = 0.65 |
150% = 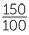 = 1 = 1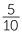 = 1.5. = 1.5. |
![]()
To write a percentage as a decimal we divide by 100. For example,
62.5% = 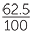 = 0.625. = 0.625. |
Writing fractions and decimals as percentages
Fractions with a denominator of 100 are written easily as percentages.
For example,
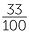 = 33% = 33% |
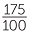 = 175%. = 175%. |
To write a fraction as a percentage, first see if it is possible to find an equivalent fraction with a denominator of 100.
For example,
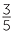 = = 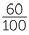 = 60% = 60% |
 = = 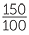 = 150%. = 150%. |
When a fraction does not have an equivalent fraction with a denominator of 100, multiply the fraction by 100%. This does not change the fraction as 100% =  = 1.
= 1.
For example,  =
=  × 100% =
× 100% = 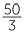 % = 16
% = 16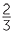 %.
%.
Similarly, to write a decimal as a percentage multiply by 100%.
![]() 0.6 = 0.6 × 100% = 60%
0.6 = 0.6 × 100% = 60%
![]() 3.2 = 3.2 × 100% = 320%
3.2 = 3.2 × 100% = 320%
We proved the following earlier:
Every rational number can be written as a terminating or recurring decimal, and vice versa.
- The decimal is terminating if and only if the fraction in simplest form has a denominator that is a product of 2’s and 5’s only.
- If the decimal doesn’t terminate, it eventually repeats with the length of the repeating block less than the denominator.
It is also true that every real number has a decimal expansion (representation). If the real number is not rational then the expansion is infinite and not recurring. The representation is not always unique. For example, the decimal 1.5 can also be expressed as 1.4999999…..
We can state this more precisely.
- Every real number x has a decimal expansion. The decimal expansion is unique (if we ignore ending zeros) unless x is a non-zero terminating decimal, in which case x has exactly two decimal expansions, one terminates and one ending in an infinite tail of nines.
- Conversely every decimal expansion specifies a real number.
EXAMPLE
Consider the infinite decimal that starts with 0.101 and continues with two 0’s and a 1, three 0’s and a 1 and so on.
0.101001000100001…
This decimal expansion is neither terminating nor recurring. This decimal does not represent a fraction.
In other modules we will discuss numbers that are not rational.
These are called irrational numbers.
Converting a repeating decimal to a fraction
A method for writing repeating decimals as fractions is shown in the following example.
EXAMPLE
Write 0.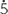
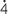 as a fraction.
as a fraction.
Solution
Let x = 0.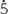
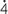 . So x = 0.545454… Multiply by 100
. So x = 0.545454… Multiply by 100
![]() 100x = 54.545454545….
100x = 54.545454545….
Subtracting x = 0.5454… from both sides
| 99x | = 54 | |
| x | = 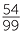 |
|
= 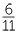 |
EXERCISE 3
Write 0.36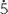
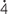 as a fraction.
as a fraction.
Any real number can be approximated to any desired accuracy by a rational number.
This can be seen as follows.
Every real number x has a decimal expansion. To approximate x within ±10−n, truncate that expansion at the nth decimal place. The result is a finite decimal, and so represents a fraction, and by subtraction the difference is less than 10−n.
The number π = 3.14159……..has neither a terminating or recurring decimal representation. We can give approximations to π using decimal notation. For example π ≈ 3.142, correct to three decimal places.
There are many interesting properties of decimals. Some of these will be considered in other modules.
For example, if p is prime, and not 2 or 5, the decimal expansion of the fraction 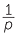 has a repeating block of length either equal to or a factor of p − 1. For example
has a repeating block of length either equal to or a factor of p − 1. For example  can be written as a repeating decimal with repeating block of length 6.
can be written as a repeating decimal with repeating block of length 6.
 Decimal fractions had been employed for the extraction of square roots by Islamic mathematicians such as Al-Kashi (1380 − 1429) and also by the Chinese at an even earlier time.
Decimal fractions had been employed for the extraction of square roots by Islamic mathematicians such as Al-Kashi (1380 − 1429) and also by the Chinese at an even earlier time.
The introduction of decimal fractions as a common computational practice can be dated back to the Flemish pamphlet De Thiende (36 pages), published at Leyden in 1585, together with a French translation, La Disme, by the Flemish mathematician Simon Stevin (1548-1620), then settled in the Northern Netherlands. No one realized their widespread potential for their daily use before Stevin. He felt that this innovation was so significant, that he declared the universal introduction of decimal coinage, measures and weights to be merely a question of time.
Stevin’s notation was, however, rather unwieldy. The point separating the integers from the decimal fractions seems to be the invention of Bartholomaeus Pitiscus who used it in his trigonometrical tables (1612). It was also used by John Napier in his logarithmic papers (1614 and 1619).
It should be noted that the Babylonians used a sexagesimal system. That is, instead of the ‘places’ of the decimal system they used ‘places’  ,
, 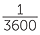 etc., This is recorded for instance on Plimpton 322 which was written in about 1800BC.
etc., This is recorded for instance on Plimpton 322 which was written in about 1800BC.
The equivalent to the decimal point did not occur in Babylonian writings until much later
(c 300 BC).
Long before decimals were used, the need to work with tenths, twentieths and hundredths was evident. Roman taxes were calculated on the basis of these types of fractions. For example, Augustus levied a tax of 1% on goods sold at auction and there was a tax of 4% on every slave sold. The Romans did not use this notation but certainly employed the concept that we use today.
The concept was used throughout the ages, however the use of the sign, % , is quite recent and its exact history uncertain.
Many different ways of multiplying have been used over the centuries. The grid (or lattice or Italian) method was used extensively. Hence we adapt it to multiply decimals.
Consider the product 24.3 × 8.96. Follow the procedure outlined below to fill in the grid. The first few numbers have been entered.
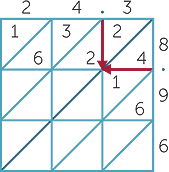 3 × 8 = 24. The 2 is placed in the top position.
3 × 8 = 24. The 2 is placed in the top position.
4 × 8 = 32. The 3 is placed in the top position.
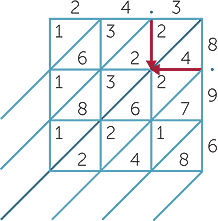 Notice the arrows in the grid extending inwards
Notice the arrows in the grid extending inwards
from the decimal points. The diagonal on which these arrows meet (shown as a bold line) separates numbers greater than or equal to 1 from numbers less than 1. Now fill in the grid and extend the diagonal as shown below.
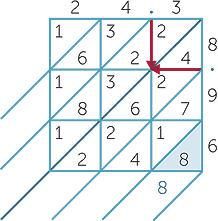 Next, add along the diagonals, starting at the bottom right.
The sum for the first diagonal is 8. This 8 represents
Next, add along the diagonals, starting at the bottom right.
The sum for the first diagonal is 8. This 8 represents  .
.
Check your answers using another method for long multiplication.
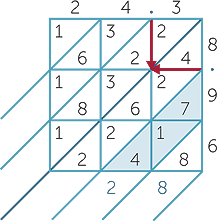 The sum for the second diagonal is 7 + 1 + 4 = 12.
The sum for the second diagonal is 7 + 1 + 4 = 12.
This 12 represents  =
= 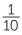 +
+  . The 1 is carried to
. The 1 is carried to
the next diagonal.
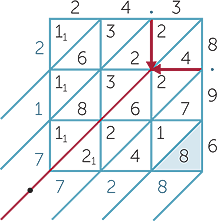 The grid is now complete. The answer is 217.728.
The grid is now complete. The answer is 217.728.
Note that the decimal point in the answer appears
at the end of the red diagonal.
EXERCISE 4
Try these problems using this method
| a | 0.234 × 0.896 | b | 4.567 × 8.32 | c | 6.892 × 5.789 |
Man and Number, Donald Smeltzer, Adam and Charles Black, London, (1965)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
The Babylonian tablet Plimpton 322, Bill Casselman, https://www.math.ubc.ca/~cass/courses/m446-03/pl322/pl322.html
Exercise 1
a![]()
 - terminating − 0.04
- terminating − 0.04
b![]()
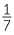 - recurring − 0.
- recurring − 0.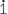 4285
4285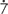
c![]()
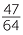 - terminating − 0.734375
- terminating − 0.734375
d![]()
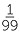 - recurring − 0.
- recurring − 0.
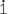
Exercise 2
a![]() 0.
0.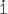
b![]() 0.
0. 2
2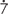
c![]() 0.
0. 0
0
d![]() 0.
0. 7
7
Exercise 3
a![]()

Exercise 4
a![]() 0.209664
0.209664
b![]() 37.99744
37.99744
c![]() 39.897788
39.897788
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


