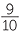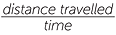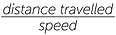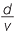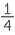The Improving Mathematics Education in Schools (TIMES) Project
- Fluency with addition, subtraction, multiplication and division of whole numbers
and fractions. - An understanding of equivalent fractions.
- Familiarity with the basic units of distance, time, mass and volume.
We encounter many different kinds of rates in everyday life. There are two types of rates which are considered in this module.
Constant rates
Examples of constant rates are:
- Mary earns $15 an hour working at the supermarket.
- Flour costs $4.50 a kilogram.
- A car travels at a constant speed of 60 km/h between two points on a road.
Average rates
Examples of average rates are:
- The Smith household uses 500 litres of water per day over a period of 3 months.
- A swimmer does an average 30 laps an hour in training sessions.
- Paul travels at an average speed of 60 km per hour over a period of 2 hours.
The rate of change of the ‘500 litres per day’ is probably determined by finding a quotient

The rate of ‘30 laps an hour’ is determined in a similar way.
The concept of instantaneous rate is introduced through calculus in Year 11. An example of instantaneous rate of change is the speed recorded by a speedometer in a car. If the speedometer is registering 60 km/h, we can say that we are travelling at 60 km per hour
at that particular instant.
Ratios are used to compare two or more like quantities. For example:
- Salad dressing may be made using the ratio 1 : 2 by volume of vinegar to oil (one part vinegar to two parts oil).
- An alloy consists of metals silver, lead and zinc in the ratio 1 : 2 : 5 by mass (one part
silver to two parts lead to five parts zinc).
When we work with fractions and percentages, the emphasis is on the relationship between a part and the whole. For ratios the emphasis is usually on the relationship between parts of the whole.
For example, in a group of 50 students, 20 are girls and 30 are boys. Two fifths of the students are girls and three fifths are boys is the natural use of fractions. The ratio of boys to girls is three to two or the ratio of girls to boys is two or three. Ratios are a different way of showing the relationship between the number of girls and the number of boys.
Another common example is the weight ratio of water to cement used in mortar, which is commonly stated as 1 : 4. This means that the weight of cement used is four times the weight of water used. Without further information, it does not say anything about the total amounts of cement and water used, nor the amount of mortar being made.
The ratios discussed in this module mostly involve fractions (rational numbers) or whole numbers.
Many practical problems can be solved by working with ratios in appropriate ways. Using a familiar and simple idea − the unitary method − many problems involving rates and ratios can be solved. This method is discussed in the module, The Unitary Method.
It is more convenient to deal with ratios first.
Ratios provide a way of dealing with relative sizes. They are closely related to fractions, but in many problems they are more convenient to use than fractions.
For example, suppose that I mix 200 ml of cordial and 700 ml of water in a jug. The mixture then contains two parts of cordial to every seven parts of water. This is written as:
| cordial : water = 2 : 7 | (Read this as ‘The ratio of cordial to water is 2 to 7.’) | |||
or as |
water : cordial = 7 : 2 |
(Read this as ‘The ratio of water to cordial is 7 to 2.’) |
In this example, ‘one part’ is 100 mL. Another mixture of identical strength could be made by taking ‘one part’ to be 1 L, and mixing 2 L of cordial with 7 L of water. This idea of parts is very useful in dealing with problems involving ratios.
Now consider an example involving ratios of lengths. The diagram below shows two ribbons, a blue one that is 30 cm long, and a white one 50 cm long.
![]()
Taking ‘one part’ to be 10 cm, we can write
![]() length of blue ribbon : length of white ribbon = 3 : 5.
length of blue ribbon : length of white ribbon = 3 : 5.
Now suppose that we join the two ribbons together to make a single ribbon of length
80 cm, as shown.
![]()
| Then | length of blue ribbon : total length = 3 : 8 | |
or as |
length of white ribbon : total length = 5 : 8 |
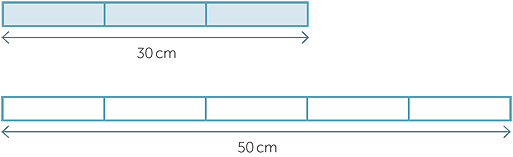
We can also write that the blue section is  of the total length, and the white section is
of the total length, and the white section is 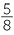 of the total length.
of the total length.
EXAMPLE
A bag of bread rolls contains 13 wholemeal rolls and 9 multigrain rolls. Write down:
a![]() the ratio of the number of wholemeal rolls to the number of multigrain rolls.
the ratio of the number of wholemeal rolls to the number of multigrain rolls.
b![]() the ratio of the number of multigrain rolls to the number of wholemeal rolls.
the ratio of the number of multigrain rolls to the number of wholemeal rolls.
c![]() the ratio of the number of wholemeal rolls to the total number of rolls.
the ratio of the number of wholemeal rolls to the total number of rolls.
Solution
a![]() number of wholemeal rolls : number of multigrain rolls = 13 : 9
number of wholemeal rolls : number of multigrain rolls = 13 : 9
b![]() number of multigrain rolls : number of wholemeal rolls = 9 : 13
number of multigrain rolls : number of wholemeal rolls = 9 : 13
c![]() number of wholemeal rolls : total number of rolls = 13 : 22
number of wholemeal rolls : total number of rolls = 13 : 22
EXAMPLE
A mixture contains 200 ml of milk and 500 ml of water. What is the ratio of milk to water?
Solution
We will solve this problem using the idea of parts. We will take 100 ml as one part.
200 ml of milk = 2 parts, each of 100 ml
500 ml of water = 5 parts, each of 100 ml
Hence the ratio of milk to water = 2 : 5.
In the following examples, we will explore the link between ratios and fractions.
EXAMPLE
An alloy of gold and silver contains 2 parts of gold to 5 parts of silver by mass.
a![]() What fraction of the alloy is gold?
What fraction of the alloy is gold?
b![]() What fraction of the alloy is silver?
What fraction of the alloy is silver?
c![]() How much of each metal does 700 g of the alloy contain?
How much of each metal does 700 g of the alloy contain?
Solution
a![]() There are 2 + 5 = 7 parts in the alloy, 2 of which are gold.
There are 2 + 5 = 7 parts in the alloy, 2 of which are gold.
![]() Hence fraction of gold =
Hence fraction of gold = 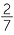 .
.
b![]() There are 5 parts of silver in the alloy.
There are 5 parts of silver in the alloy.
![]() Hence fraction of silver =
Hence fraction of silver = 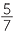 .
.
c![]() We will take 100 g as one part.
We will take 100 g as one part.
![]() There are 200 g of gold and 500 g of silver.
There are 200 g of gold and 500 g of silver.
EXAMPLE
One-tenth of the population has red hair. What is the ratio of the number of redheads to the rest of the population?
Solution
| Rest of the population | = 1 −  |
|
= |
Divide the population into 10 parts, each consisting of  of the population.
of the population.
So the ratio of redheads to the non-redheads in the population is 1 : 9.
EXERCISE 1
In a class of 32 students, 13 students study German and no other language, 9 study French and no other language, 3 students study both French and German and 7 do not study French or German.
a![]() Draw a Venn diagram showing this information
Draw a Venn diagram showing this information
b![]() What is the ratio of students who study French and German to those who study neither?
What is the ratio of students who study French and German to those who study neither?
c![]() What is the ratio of students who study French or German to those who study neither?
What is the ratio of students who study French or German to those who study neither?
Ratios with three or more terms
Many problems involve a mixture of more than two things. For example, when making a cake, we generally mix flour, sugar, butter and milk.
A streamer is made by joining three grey ribbons, four white ribbons and two blue ribbons, all of equal length.

There are three parts of grey, four parts of white and two parts of blue, so we say that the ratio of grey to white to blue is
![]() grey : white : blue = 3 : 4 : 2.
grey : white : blue = 3 : 4 : 2.
EXAMPLE
A batch of concrete is made from 10 kg of sand, 2 kg of cement, 5 kg of water and 2 kg of gravel. Express the parts as a ratio and express each ingredient as a fraction of the whole.
Solution
sand : cement : water : gravel = 10 : 2 : 5 : 2
The concrete contains 10 parts of sand to 2 parts of cement to 5 parts of water to 2 parts of gravel. There are 19 parts altogether, each part being 1 kg of material, so:
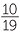 of the concrete is sand
of the concrete is sand of the concrete is cement
of the concrete is cement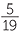 of the concrete is water
of the concrete is water of the concrete is gravel.
of the concrete is gravel.
Using ratios to find quantities
An alloy of gold and silver contains 2 parts of gold to 5 parts of silver by mass. That is, the ratio of gold to silver by mass is 2 : 5
How much of each metal does 700 g of the alloy contain?
There are 2 parts of gold to 5 parts of silver by mass. There are 2 + 5 = 7 parts in total.
Take each part to be 100 g.
2 parts = 200 g and 5 parts = 500 g.
There are 200 g of gold and 500 g of silver.
Note: If a quantity is divided in the ratio a : b it is natural to work with a + b parts.
EXAMPLE
A man divides his estate of $360 000 in the ratio 4 : 3 : 3 amongst his daughter and his two sons. How much does each receive?
Solution
There are 4 + 3 + 3 = 10 parts in total.
10 parts = $360 000
1 part = $36 000
3 parts = $108 000
4 parts = $144 000
Hence the daughter receives $144 000 and each son receives $108 000.
EXERCISE 2
Students in a school are told to choose one out of three sports options: tennis, basketball or swimming. Given that the pupils choose the options in the ratio 4 : 2 : 3 and that 120 choose tennis, find:
a ![]() the number of pupils in the school
the number of pupils in the school
b![]() the number of students who choose swimming
the number of students who choose swimming
Reducing a ratio to lowest terms
A ratio involving whole numbers can be reduced to lowest terms − just like a fraction − by dividing all the terms in the ratio by their highest common factor (HCF). Sometimes doing this can make it easier to understand the situation we are looking at, as in the next example.
Definition Two ratios are equivalent (equal ratios) if one is obtained from the other by multiplying or dividing all of the quantities by the same non-zero number.
Equivalent ratios behave like equivalent fractions. 1 : 3 = 2 : 6 = 3 : 9 = 4 : 12 and so on.
EXAMPLE
A mixture contains 6 parts of oil, 2 parts of insecticide and 10 parts of water by volume. Express the ratio of
![]() oil : insecticide : water
oil : insecticide : water
in lowest terms.
Solution
| oil : insecticide : water | = 6 : 2 : 10 | |
= 3 : 1 : 5 |
In other cases, we may need to find a common denominator for a set of fractions, so that we can easily compare them.
EXAMPLE
Eliminate fractions in the ratio 4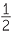 : 3, and then reduce it to lowest terms.
: 3, and then reduce it to lowest terms.
Solution
4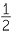 : 3 : 3 |
= 9 : 6 | (Multiply by 2) | ||
| = 3 : 2 | (Divide by 3) |
EXERCISE 3
a![]() Prove that a : b = c : d if and only if
Prove that a : b = c : d if and only if  =
=  .
.
b![]() Prove that if a : b = c : d, then (a + b): b = (c + d): d .
Prove that if a : b = c : d, then (a + b): b = (c + d): d .
c![]() Prove that if a : b = c : d, then (a − b): b = (c − d): d .
Prove that if a : b = c : d, then (a − b): b = (c − d): d .
Rates are a measure of how one quantity changes for every unit of another quantity.
For example:
- 50 km/h means that a car travels 50 km in one hour.
- 20 litres/minute means 20 litres of water flows in one minute.
- $5 per kilogram means that one kilogram costs $5.
- 30 km/litre means that a vehicle travels 30 km on one litre (of fuel).
In each of these examples we are assuming a constant rate of change.
We start with a simple example based on the rate ‘cost per unit’ and use the unitary method.
EXAMPLE
If 12 mangoes cost $27, how much do 7 mangoes cost?
Solution
The unit in this example is 1 mango.
| 12 | mangoes cost $27. | ||||
| 1 | mango costs $2.25. | (Divide by 12) | |||
| 7 | mangoes cost $15.75. | (Multiply by 7) |
Speed is one of the most familiar rates. Speed is a measure of how fast something is travelling. Many of the techniques introduced here can be applied in other rate situations.
Constant speed
If the speed of an object does not change over time, we say that it is travelling with constant speed.
There are three quantities associated with questions that involve constant speed. These are distance, time and, of course, constant speed. We consider three situations where information is given about two of these quantities and the third is to be determined.
- 1
- Finding the distance given a fixed speed: A car travels at a constant speed of 60 km/h.
- -
- The car travels 60 km in 1 hour.
- -
- The car travels 120 km in 2 hours
- -
- The car travels 60t kilometres in t hours.
- 2
- Finding the speed given a fixed distance : A car travels at a constant speed for 100 km.
- -
- If the car takes 1 hour to travel the 100 km, then the constant speed is 100 km/h.
- -
- If the car takes 2 hours to travel the 100 km, then the constant speed is
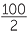 = 50 km/h.
= 50 km/h. - -
- If the car takes t hours (t > 0) to travel the 100 km, then the constant speed is
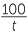 km/h.
km/h. - 3
- Finding the time given a fixed distance: A car travels 100 km.
- -
- A car travels a distance of 100 km at 100 km/h. It takes 1 hour.
- -
- A car travels a distance of 100 km at 50 km/h. It takes 2 hours.
- -
- A car travels a distance of 100 km at v km/h. It takes
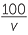 hours.
hours.
We also refer the reader to the module, Proportion, where these ideas are discussed further.
The (constant) speed (v) of a moving object is defined to be the distance (d) travelled divided by the time (t) the object takes to travel that distance:
|
speed = |
or |
v = |
||
From the above or by simple algebra: |
|
|
||
|
time taken = |
or |
t = |
||
|
distance travelled = speed × time taken |
or |
d = vt |
||
Problems about speed can be solved by either using the unitary method or using one of the three formulas above.
EXAMPLE
Mary travelled at a constant speed for 60 km and it took 4 hours to complete the journey. What was her speed?
Solution
speed =  =
= 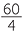 = 15 km/h.
= 15 km/h.
Average speed
When we drive a car or ride a bike, it is very rare for our speed to remain the same for a long period of time. Most of the time, especially in the city, we are slowing down or speeding up, so our speed is not constant. If we travel 20 km in 1 hour, then we say that our average speed is 20 km/h.
Average speed = 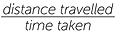
EXAMPLE
Anthony travelled at an average speed of 50 km/h for 4 hours 30 minutes. How far did
he travel?
Solution
Since distance travelled = average speed × time taken
|
The distance Anthony travelled |
= 50 × 4.5 |
|
= 225 km. |
EXAMPLE
A couple go for a walk of 12 km. They generally walk at an average speed of 3 km/h.
How long do they expect to take to complete the walk?
Solution
To solve this problem we assume constant speed.
In each hour, they walk 3 km.
The number of hours needed to walk 12 km = 4.
The couple take 4 hours to complete the walk.
EXAMPLE
A cyclist completes a circuit of 15 km. She cycles at an average speed of 12 km/h.
How long does it take her to complete the circuit?
Solution
In each hour, she cycles 12 km.
Time to cycle 15 km |
= 15 ÷ 12 |
= 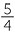 |
|
= 1 |
The cyclist takes 1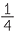 hours or 1 hour and 15 minutes to complete the circuit.
hours or 1 hour and 15 minutes to complete the circuit.
EXERCISE 4
a A boy cycles for 2 hours and 20 minutes at a constant speed of 18 km/h.
How far does he go?
b An aircraft travels 4238 km in 6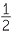 hours. What is its average speed?
hours. What is its average speed?
c A train travels for 48 km at 80 km/h. How long, in minutes, does it take?
Quantities such as 600 litres per hour, 35 km/h, $15 per m2, and $25 per litre are called rates. The unitary method sometimes makes constant rate questions quite straightforward.
EXAMPLE
Water is flowing into a dam at a constant rate of 600 litres per hour.
a How much water will flow into the dam in 2 hours?
b How much water will flow into the dam in 3.5 hours?
c How long in minutes will it take for 12 000 litres of water to flow into the dam?
d How long will it take for 10 000 litres of water to flow into the dam?
Solution
| a | 600 | litres will flow into the dam in 1 hour. | ||
| 1200 | litres will flow into the dam in 2 hours. | |||
| b | 600 | litres will flow into the dam in 1 hour. | ||
| 300 | litres will flow into the dam in half an hour. | |||
| 2100 | litres will flow into the dam in 3.5 hours. | |||
| c | 600 | litres will flow into the dam in 1 hour. | ||
| 12 000 | litres will flow into the dam in 20 hours. | |||
| d | 600 | litres will flow into the dam in 1 hour. | ||
| 100 | litres will flow into the dam in 10 minutes. | |||
| 10 000 | litres will flow into the dam in 1000 minutes. | |||
| Hence it will take 16 hours and 40 minutes for 10 000 L to flow into the dam. | ||||
Careful use of successive one-step conversions allows the units to be changed, as in the previous example. Here is another example involving two changes of units.
EXAMPLE
Van is earning $18 per hour making pancakes. How much is he earning in cents per second?
Solution
![]() Van earns $18 per hour.
Van earns $18 per hour.
![]() Van earns 1800 cents per hour.
Van earns 1800 cents per hour.
![]() Van earns 30 cents per minute.
Van earns 30 cents per minute.
![]() Van earns
Van earns 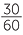 cents per second = half a cent per second.
cents per second = half a cent per second.
Constant rates are related to linear graphs that pass through the origin. A gradient is the ratio rise: run which is usually written  .
.
For example, the graph of distance travelled against time for a particle travelling at constant speed is a straight line passing through the origin. The gradient of the line has the same value as the constant speed.
If you plot the equivalent ratios 1:2 = 2:4 = ….. as ordered pairs (1, 2), (2, 4), they, of course, all lie on a straight line of gradient 2 passing through the origin. This will be discussed further in the module, Proportion.
Ratios lead to and interact with many topics. In years 7 − 10 this includes:
- The fixed ratio Circumference : diameter = π : 1
- The trigonometric ratios, for example sin x =
 .
. - Similar triangles. The ratio of matching side lengths is a constant.
Rates also occur in financial mathematics in such areas as exchange rates and interest rates.
Rates lead to the concept of instantaneous rates of change and hence to differential calculus.
The idea of ratio occurs naturally and ideas such as ‘twice as big’ and ‘half as long’, which are ideas of ratio would have been considered at a very early stage of human history.
Ratio is a word derived from the Latin verb ‘reri’ which means to think, estimate or calculate. It was used in the middle ages to mean computation. The medieval writers used the word ‘proportio’ to refer to what we have described in the Content section as ratio. This language is still being used today. For example ‘Divide this in the proportion 1 to 2’, which means the same as ‘Divide this in the ratio 1:2‘.
Book V of Euclid is devoted to the theory of proportion, applicable to commensurable (rational) as well as incommensurable (irrational) magnitudes. It was applicable to magnitudes of every kind (straight lines, areas, volumes, numbers, etc). This work is attributed to Eudoxus.
In Book VI of the Elements, Euclid discusses the geometric consequences and applications of ratio.
For example:
Proposition 1 (Book VI) states
‘The ratio of the areas of triangles with the same altitude is equal to the ratio of the bases of the triangles.’
Proposition 33 (Book VI) states
‘Angles subtended at the centre of a circle have the same ratio as the arcs that subtend them. Angles subtended at the circumference of a circle have the same ratio as the arcs that subtend them.’
The history of ratios and rates is resumed in the history section of the module Proportion.
Rates and ratios are applied in many areas in both commerce and science. Examples occurring in science include: velocity, acceleration, pressure, angular velocity, density, pressure and many more.
Examples occurring in commerce include: interest rates, currency exchange rates, taxation rates, unit prices, postal charges and many others.
Exercise
| 1 | a | 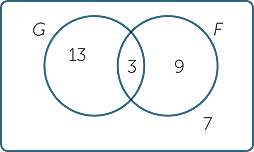 |
b | 3 : 7 | c | 25 : 7 |
| 2 | a | 270 | b | 90 |
| 3 | a | First assume that  = =  . This is equivalent to ad = bc. . This is equivalent to ad = bc. |
||
| Multiply both a and b by d in the ratio a : b to obtain ad : bd which implies | ||||
| a : b = ad : bd = bc : bd. Divide both sides of the ratio by b to obtain c : d. | ||||
| Hence a : b = c : d. | ||||
| Conversely assume a : b = c : d. There is a non-zero number k such that ak = c and bk = d. |
||||
Hence  = =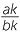 = =  . . |
||||
| b |

|
= 
|
c |

|
= 
|
|||
 + 1 + 1
|
=  + 1 + 1
|
 − 1 − 1
|
=  − 1 − 1
|
|||||
 + + 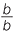
|
=  + + 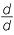
|
 − − 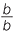
|
=  − − 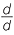
|
|||||
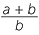
|
= 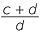
|

|
= 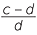
|
|||||
| (a + b) : b | = (c + d) : d | (a − b) : b | = (c − d) : d |
| 4 | a | 42 km | b | 652 km/h | c | 36 min |
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()