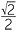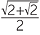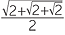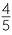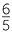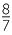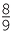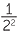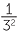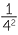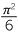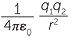The Improving Mathematics Education in Schools (TIMES) Project
- Informal experience of parts of a circle, including the radius, the diameter
and the centre. - Familiarity with the basic language of geometry including isosceles triangles
and parallelograms. - Knowledge of area and perimeter of squares, rectangles, triangles and composite figures.
- The arithmetic of fractions and decimals.
- Familiarity with simple algebraic expressions.
The circle is the most commonly seen figure whose boundary is not a straight line. Coins, plates and tables are often in the shape of a circle, and racetracks generally have semi-circular ends, while fans move in circular motion. The circular wheel is widely regarded as one of mankind’s most important inventions.
When we perform constructions, we use a ruler to draw a line and compasses to draw a circle. Lines and circles are thus fundamental in geometry.
When a wheel is rolled in the sand through one revolution, what length is traced out? This length is the distance around the circle and is called the circumference of the circle. Clearly, the larger the radius of the circle, the greater the circumference. Exactly how are the radius and circumference related?
Can we make sense of the area bounded by a circle in the same way that we define the area of a rectangle? Again it seems clear that the larger the radius of the circle, the larger the area. Exactly how are the radius of a circle and its area related?
Experimental evidence (using string) leads one to see that if the radius of a circle is doubled, then the circumference is doubled, and more generally that the circumference is proportional to the radius. This was first investigated by the Greeks who introduced the notion of a proportionality constant between the circumference and the diameter, to which we now give the symbol π (pi).
We use the term area of a circle to mean the area of the region contained within the circle. Strictly speaking, a circle together with its interior is called a ‘disc’, but we generally use the word ‘circle’ to refer both to the circle and the disc.
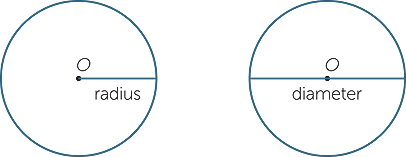
A circle is the path traced out by a point, moving in a plane, that is always a fixed distance (the radius) from a fixed point (the centre).
Any interval (or line segment) drawn from the centre of a given circle to any point
on the circle is called a radius, (plural radii).
Any interval joining two points on the circle and passing through the centre is called
the diameter of the circle.
Because every radius has the same length and every diameter has the same length, we often use the words ‘radius’ and ‘diameter’ to refer to either the interval in question or to the length of that interval. Thus the diameter of a circle is twice the radius of that circle.
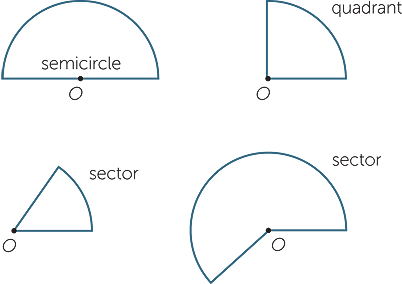
A diameter divides the circle into two congruent parts. Each part is called a semicircle. If we draw a radius perpendicular to the diameter in a semicircle, we obtain two congruent quadrants. Any two radii divide the circle into two pieces. Each piece is called a sector (from the Latin word secare − to cut).
The circumference of a circle is the distance around the circle. The ancients, probably by using string, discovered that doubling the diameter of a circle, doubled the circumference; trebling the diameter, trebled the circumference and so on. In general, the circumference of a circle is proportional to its diameter.
| That is, the ratio |
 |
is the same for all circles. We represent this constant ratio by the Greek letter π, (pronounced ‘pie’). Thus in every circle,
 |
= π |
Rearranging this formula we obtain
C = πd,
where C is the circumference and d is the diameter of the circle. Since the diameter is twice the radius, we can also write
C = 2πr,
where r is the radius of the circle.
The number π is not a whole number, nor is it a rational number. Its approximate value, correct to 7 decimal places, is 3.1415927, but the decimal expansion of π continues forever with no apparent pattern. This number is one of the most remarkable of all numbers in mathematics and reappears somewhat mysteriously in many places.
We usually round it off to two decimal places as 3.14. If greater accuracy is required,
we can take more decimal places.
Although π is not a rational number (this is not easy to prove), it is close to the rational number 3 =
= 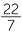 . Written as a decimal 3
. Written as a decimal 3 = 3.
= 3.![]() 4285
4285![]() , so 3
, so 3 differs from π only in its third decimal place. This approximation is often used in situations where we wish to avoid decimals.
differs from π only in its third decimal place. This approximation is often used in situations where we wish to avoid decimals.
When solving problems involving π, it is best to leave the number in terms of π until the end of the problem and then, if required, use an approximation.
EXAMPLE
Find the circumference of a circle:
a![]() whose diameter is 14 cm
whose diameter is 14 cm![]() b
b ![]() whose radius is 21 cm
whose radius is 21 cm
Give each answer:
i![]() in terms of π
in terms of π ![]()
![]()
![]() ii
ii![]() as an approximate value, using π ≈
as an approximate value, using π ≈ 
iii ![]() as an approximate value using π ≈ 3.14.
as an approximate value using π ≈ 3.14.
Solution
| a | i | C | = πd | b | i | C | = 2πr | |||||
| = 14π | = 2 × π × 21 | |||||||||||
| = 42π cm | ||||||||||||
| ii | C | = 14π | ii | C | = 42π | |||||||
≈ 14 × 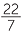 |
≈ 42 × 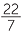 |
|||||||||||
| = 44 cm | = 132 cm | |||||||||||
| iii | C | = 14π | iii | C | = 42π | |||||||
| ≈ 14 × 3.14 | ≈ 42 × 3.14 | |||||||||||
| = 43.96 cm | = 131.88 cm | |||||||||||
Note that the answers in parts ii and iii are only approximate, since we have used an approximation for π.
EXERCISE 1
The figure is obtained by removing the two semicircles from the large semicircle.
What is the perimeter of the shaded region?
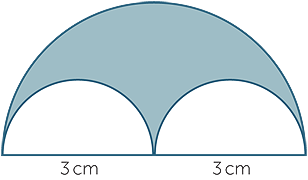
EXERCISE 2
A circle has circumference 50π cm. Find the radius of the circle.
In the module, Introduction to Measurement we defined the area of a rectangle, with sides of length l and w, by the formula A = lw. We then used this formula, together with dissection arguments, to find the area of other figures bounded by straight lines,
A circle has a curved boundary, so arguments based on rectangles and a finite number of dissections cannot be used. Without calculus, we cannot give a rigorous proof of the well-known formula for the area of a circle A =πr2, given that C = 2πr, but we can give a reasonably convincing argument using intuitive ideas about limits.
Indeed it is even unclear how the area of a circle should be defined — but we can give a reasonably convincing argument using intuitive ideas about limits.
The first step is to approximate the area of a circle using a regular polygon. We inscribe a regular polygon in the circle and split up the polygon into congruent isosceles triangles as shown below.

We can define the area of the circle as the limit of the sum of the areas of the triangles as the number of triangles increases. This idea can now be used to find the formula for the area of the circle with radius r.
Dissect the polygon into congruent isosceles triangles and arrange them alternately as shown in the diagram below. Since the triangles are isosceles and congruent, the opposite sides of this quadrilateral are equal and so it is a parallelogram.
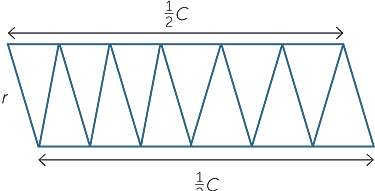
As the number of sides of the polygon increases, and with it the number of triangles, the height of the parallelogram gets as close as you like to the radius r of the circle. Moreover, the base of each triangle becomes very close to the curved arc of the circle, so the length of the parallelogram is very close to half the circumference, C. Hence the limit of the area of the parallelogram is
A = r × 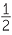 × C = r ×
× C = r × 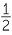 × 2πr = πr2
× 2πr = πr2
Thus we may take the area of the circle to be given by the well-known formula
A = πr2.
EXAMPLE
- a
- Find the area of a circle whose radius is 7 cm, giving your answer in terms of π.
- b
- Find the area of a circle whose diameter is 7 cm, using the approximate π ≈
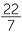 .
. - c
- Find the area of a circle whose whose radius is 30 cm , using the approximation
π ≈ 3.14.
Solution
| a | A | = πr2 | b | Since the diameter is 7 cm, the radius is  cm cm |
||||
| = 49π cm2. | A | = πr2 | ||||||
= 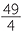 π π |
||||||||
≈ 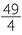 × × 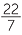 |
||||||||
= 38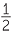 cm2. cm2. |
||||||||
| c | A | = πr2 | ||||||
| = 900π | ||||||||
| ≈ 900 × 3.14 | ||||||||
| = 2826 cm2. | ||||||||
EXERCISE 3
The Greeks avoided π by expressing the area in terms of the circumference.
- a
- Express the area of a circle radius r in terms of it's circumference C.
- b
- A circle has circumference 12 cm. Find its area.
EXERCISE 4
An alternate way to ‘discover’ the area of a circle is as follows.
Imagine that a circle of radius r is made up of a large number of concentric circular pieces of very thin string. The circles are then cut along a radius, and the pieces of string are straightened out and laid one on top of the other as shown in the diagram below to form a shape which is approximately a ‘triangle’.

- a
- Find the base and height of the triangle in terms of r.
- b
- Deduce the formula for the area of the circle.
We can use addition and subtraction of areas to find the area of more complicated figures.
EXAMPLE
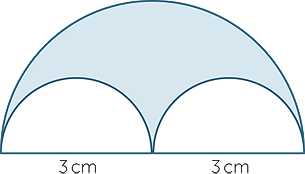 Find the area of the shaded region.
Find the area of the shaded region.
SOLUTION
| The area of the large semicircle | =  × π × 32 = × π × 32 = 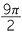 |
| The area of a small semicircle | = 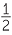 × π × × π ×  |
=  cm2 cm2 |
|
=  − 2 × − 2 ×  |
|
= 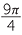 cm2 cm2 |
EXERCISE 5
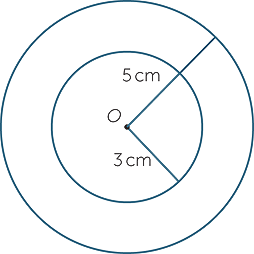 Find the white area enclosed between the circles in the diagram below. The smaller circle has radius 3 cm, while the larger has radius 5 cm.
Find the white area enclosed between the circles in the diagram below. The smaller circle has radius 3 cm, while the larger has radius 5 cm.
Such a region is called an annulus.
EXERCISE 6
A figure consisting of a rectangle of length 8 cm and width 7 cm and two quarter-circles of radius 7 cm is cut from a piece of cardboard.

- a
- Find the area of the figure in terms of π.
- b
- Find the approximate area of the figure, using π ≈ 3.14.
EXERCISE 7

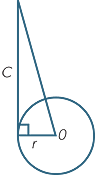
- a
- ABC is a right-angled triangle with right angle B. The circle shown is the incircle of the triangle. Find the radius, r, of the incircle.
- b
- Find the radius of the incircle of a right-angled
triangle with sides 5, 12 and 13. - c
- Find the radius of the incircle of a right-angled
triangle with sides a, b and c, where c is the length of the hypotenuse.
Students need to understand the natural generalisation of the circle to three dimensions, the sphere.
By 240 BC Archimedes proved that the volume of the sphere of radius r is 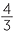 πr3 and that its surface area is 4πr2. This was a remarkable achievement at the time. Spheres are of great importance. The earth is approximately spherical and calculating distances on a sphere is an important problem in navigation, linked to a branch of mathematics known
πr3 and that its surface area is 4πr2. This was a remarkable achievement at the time. Spheres are of great importance. The earth is approximately spherical and calculating distances on a sphere is an important problem in navigation, linked to a branch of mathematics known
as spherical geometry.
We usually measure angles in degrees, for example, 90° in a right-angle, or 360° is a full revolution. This is mainly for historical reasons — the Babylonians used a base-60 number system and for example we still use 60 minutes in a degree. Radian measure is crucial in later work on calculus. The idea is to define an angle so its size is the same as the size of the arc subtends it at the centre in a circle of unit radius. An alternative system is to measure angles in radians.
Let O be the centre of a circle of radius 1.
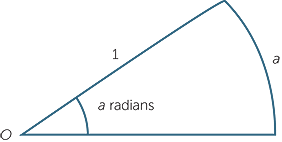
Since the angle in a straight line is 180° (in degrees) and is subtended by an arc of length π in the unit circle, 180° = π radians. From this, other angles can be represented as multiples of π. For example, an angle of 45° =  radians, and an angle of 30° =
radians, and an angle of 30° =  radians.
radians.
The search for the circumference and area of a circle goes back into antiquity. For example, we read in 1 Kings 7:23, And he made a molten sea ten cubits from the one brim to the other, round in compass... and a line of thirty cubits did compass it round about. Assuming the ‘sea’ is circular, this gives the value of π as 3. Even earlier, the Babylonians gave the (incorrect) formula A = 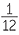 C2 for the area of a circle in terms of the circumference. This also gives π = 3.
C2 for the area of a circle in terms of the circumference. This also gives π = 3.
The Egyptians used the (incorrect) formula A = 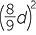 , where d is the diameter of the circle. This gives π =
, where d is the diameter of the circle. This gives π = 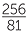 ≈ 3.164099 − not a bad approximation. Islamic mathematics in the Middle Ages used the approximation π ≈
≈ 3.164099 − not a bad approximation. Islamic mathematics in the Middle Ages used the approximation π ≈ ![]() because
because ![]() = 3.1622….
= 3.1622….
 The Greeks, notably Euclid, showed that ‘Circles are to one another as the squares on the diameters’, which tells us that the area of a circle is proportional to the square of the radius. Later, Archimedes (287-212 BC) proved the theorem: ‘The area of any circle is equal to the area of a right triangle in which one of the legs is equal to the radius and the other to the circumference’, which is similar to our informal derivation of the formula for the area of a circle in the Content section above.
The Greeks, notably Euclid, showed that ‘Circles are to one another as the squares on the diameters’, which tells us that the area of a circle is proportional to the square of the radius. Later, Archimedes (287-212 BC) proved the theorem: ‘The area of any circle is equal to the area of a right triangle in which one of the legs is equal to the radius and the other to the circumference’, which is similar to our informal derivation of the formula for the area of a circle in the Content section above.
In all of these expressions, the need for the symbol π was suppressed by expressing the area in terms of the radius and the circumference. The letter π was chosen in the early 18th century because it is the first letter of the Greek word for perimeter (perimetron).
Archimedes was also the first to make a serious attempt to estimate π. He inscribed circles in regular polygons. By using a 96-sided polygon, he proved that 3 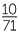 < π < 3
< π < 3 . (You can check to see how good or bad an approximation this is.)
. (You can check to see how good or bad an approximation this is.)
For centuries, the number π was linked exclusively to circles, spheres and cones.
In 1593, using polygons and some geometry, Francois Viète showed that
|
which gives an analytic ‘definition’ for π as the limit of a product, but is essentially independent of the circle.
In 1655 came the surprising Wallis’ product:
|
While we could define π using either of these formulas, neither is particularly good for actually approximating π correct to many decimal places.
Using the formula
|
Machin (1706) calculated π by hand correct to 100 decimal places. This has, needless to say, been greatly improved upon and modern methods give π correct to billions of decimal places.
The number π turns up in mathematics in many places where it might not, a priori, be expected to appear. One such instance is the remarkable infinite sum
|
that was discovered by Euler about 1730.
Coulomb’s law in Physics, states that the magnitude of the electrostatic force F on a charge q1 due to the presence of a second charge q2, is given by
F = |
|
where ε0 is a constant, and r is the distance between the two charges.
This is one of many formulas in science in which π appears.
The number π continues to fascinate and challenge mathematicians. We know that it is an irrational number and we suspect that its digits are statistically random − but no proof of this has yet been found.
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
EXERCISE 1
6π cm
EXERCISE 2
25 cm
EXERCISE 3
a![]()
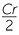
![]() b
b![]()
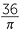 cm2
cm2
EXERCISE 4
Base = 2πr and height = r.
Area of triangle = πr2.
EXERCISE 5
16π cm2
EXERCISE 6
a![]() (56 +
(56 + 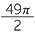 ) cm2
) cm2
b![]() 132.93 cm2
132.93 cm2
EXERCISE 7
a![]() r = 1
r = 1 ![]() b
b![]() r = 2
r = 2 ![]() c
c![]()
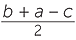
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()