The Improving Mathematics Education in Schools (TIMES) Project
Year : 7
It is assumed that in Years 1-6, students have had many learning experiences that consider simple and everyday events involving chance, and descriptions of them. They have considered which events are, or may be assumed, more or less likely, and, if events are not more or less likely than others, then they have considered that it is reasonable to assume the events to be equally-likely. They have looked at simple everyday events where one cannot happen if the other happens, and, in contrast, they have thought about simple situations where it is reasonable to assume that the chance of occurrence of an event is not changed by the occurrence of another. They recognise impossible and certain events, and that probabilities range from 0 to 1. They have listed outcomes of chance situations for which equally-likely outcomes may be assumed. They have represented probabilities using fractions, decimals and percentages. They have had hands-on, real and virtual learning experiences in how probabilities can affect observations in both small and larger amounts of data (real and virtual), and have compared observed frequencies with expected frequencies corresponding to given or assumed sets of probabilities.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
Statistics is the science of variation and uncertainty. Concepts of probability underpin all of statistics, from handling and exploring data to the most complex and sophisticated models of processes that involve randomness. Statistical methods for analysing data are used to evaluate information in situations involving variation and uncertainty, and probability plays a key role in that process. All statistical models of real data and real situations are based on probability models. Probability models are at the heart of statistical inference, in which we use data to draw conclusions about a general situation or population of which the data can be considered randomly representative.
Probability is a measure, like length or area or weight or height, but a measure of the likeliness or chance of possibilities in some situation. Probability is a relative measure; it is a measure of chance relative to the other possibilities of the situation. Therefore, it is very important to be clear about the situation being considered. Comparisons of probabilities − which are equal, which are not, how much bigger or smaller − are therefore also of interest in modelling chance.
Where do the values of probabilities come from? How can we “find” values? We can model them by considerations of the situation, using information, making assumptions and using probability rules. We can estimate them from data. Almost always we use a combination of assumptions, modelling, data and probability rules.
The concepts and tools of probability pervade analysis of data. Even the most basic exploration and informal analysis involves at least some modelling of the data, and models for data are based on probability. Any interpretation of data involves considerations of variation and therefore at least some concepts of probability.
Situations involving uncertainty or randomness include probability in their models, and analysis of models often leads to data investigations to estimate parts of the model, to check the suitability of the model, to adjust or change the model, and to use the model for predictions.
Thus chance and data are inextricably linked and integrated throughout statistics. However, even though considerations of probability pervade all of statistics, understanding the results of some areas of data analysis requires only basic concepts of probability. The objectives of the chance and probability strand of the F-10 curriculum are to provide a practical framework for experiential learning in foundational concepts of probability for life, for exploring and interpreting data, and for underpinning later developments in statistical thinking and methods, including models for probability and data.
In this module, in the context of understanding chance and its effects in everyday life, we build on the preliminary concepts of chance of Years 1-6 to focus more closely on how probabilities are assigned in simple and familiar situations.
Situations in which equally-likely outcomes can be assumed are re-visited to focus more closely on assigning and determining probabilities of events, along with new situations in which students can readily collect data to investigate assumptions of equally-likely outcomes of experiments.
The emphasis in this module is on consolidation of learning experiences in situations involving assumptions of equally-likely probabilities and their use in assigning probabilities to events, before moving on to describing more general events, and thence to assigning and estimating probabilities in more general situations.
Concepts, assumptions and effects of probability on observations are experienced through examples of situations familiar and accessible to Year 7 students and that build on concepts and experiences introduced in Years 1-6.
Assuming equally-likely outcomes
As always, we need to clearly identify the situation and describe the outcomes so that there is no confusion and anyone reading or hearing our description will be thinking of the events in the same way as us. Sometimes it is very easy to describe possible events and sometimes there is really only one way of describing them, but in many situations this is not so and careful description is therefore important.
Once we have described the situation and its outcomes, we can then think about the probabilities. This often requires us to think about which outcomes or events could be assumed to be equally-likely. For a (finite) number of equally-likely outcomes of a simple and everyday situation, we can assign the equal probabilities as 1/(total number of outcomes). Sometimes it is straightforward to be able to assume equally-likely and sometimes the assumptions may need more careful identification.
Understanding the effects of assumptions on probabilities and the effects of probabilities on real observations requires a sound sense of the size of the probabilities. This sense can often be heightened by different expressions for probabilities − as fractions, decimals or percentages. Some people have a preference amongst these, but for many people it is useful to be able to move between these. Hence in the examples below, the probabilities may be expressed in any of these three forms.
We will consider situations in which the description of the outcomes is straightforward and assignation of values for the probabilities is also straightforward, with the assumptions being readily accessible for Year 7.
Example A: Throwing one die
Many board games use throws of one or two dice to give how many places to move or what choice is to be made. The usual single die has 6 sides, with each side having a number of marks giving its face value of one of the values 1, 2, 3, 4, 5 or 6. So the outcomes of a throw or toss of a single die are very simple to describe and there is really no other way of describing the outcome except as the face value of the uppermost face when the die lands, and hence the list of possible outcomes is simply the set of numbers (1, 2, 3, 4, 5, 6).
If the die is fair and is well shaken in some container before throwing it, there is no reason not to assume equally-likely probabilities for the 6 face values. Hence each face value has a chance of 
of appearing on one throw of a die.
If one or more faces are more likely to come up than others, the die is called a “loaded” die.
Example B: Throwing two dice
Many board games use throws of two dice. Again it is simple to describe the basic outcomes of throws of a pair of dice tossed together. The basic outcomes are pairs of numbers, where each number is the face value of the uppermost face of one of the dice. We will consider two different coloured dice or two dice that are marked in some way so that we can tell them apart. The list of possible outcomes is the list of pairs of numbers from 1 to 6, where the first number in each pair is the uppermost face of die 1 (for example, this might be a red die) and the second number in each pair is the uppermost face of die 2 (for example, this might be a blue die) as follows:
(1, 1), (1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (1, 5), (5, 1), (1, 6), (6, 1), (2, 2), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2),
(2, 6), (6, 2), (3, 3), (3, 4), (4, 3), (3, 5), (5, 3), (3, 6), (6, 3), (4, 4), (4, 5), (5, 4), (4, 6), (6, 4), (5, 5), (5, 6), (6, 5), (6, 6).
If both dice are fair and they are well shaken in a container before throwing, there is no reason not to assume that each of the above 36 outcomes is equally-likely. So we would assume that each of the ordered pairs of numbers have a chance of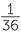 
of appearing when we throw two fair different coloured dice.
Example C: Which ticket will be selected?
Raffles are usually run by people buying numbered (and sometimes coloured) tickets with the tickets being in two parts. The buyers keep one part and the other parts (we’ll call them the ticket stubs) are put into a container with someone picking out a ticket at random from the container. The outcomes of the draw are all the tickets that have been sold.
If the ticket stubs are well-mixed and the person making the draw does not look, then we can assume the draw is random. This means that each ticket stub is equally-likely to be drawn. Hence if 100 tickets are sold, the chance of your ticket being picked out is 
.
This is a 0.01 chance or a 1% chance.
If 1000 tickets are sold, the chance of your ticket being picked out is 
. This is a very small chance although 10 times greater than if 10,000 tickets are sold!
Example D: How good are people at choosing numbers
at random?
A teacher asks each student in a class to choose a number at random from the numbers 1 to 50. If students are able to choose at random, then for each student, each number is equally-likely to be chosen. So each number has a chance of 
or a 2% chance of being chosen.
Example E: Which destination will the contestant win for a holiday?
In a TV contest, a contestant wins a holiday in Australia. Suppose each of 10 possible destinations is placed at random behind a numbered door on a board and the contestant chooses a door. If no hints are given to the contestant, he or she is equally-likely to win any of the 10 destinations, each of which therefore has a 10% or 0.01 chance of being chosen.
Example F: Spinners
Some games, including board and other games, use spinners to give players their next moves. When spun around its pivot, the arrow of the spinner comes to rest on a segment of a circle. Usually the different segments are in different colours, so the basic outcomes of a single spin are the colours used for the different segments. If the segments are of equal size, and the spinner is given sufficient spin, there is no reason not to assume that the segments are equally-likely outcomes.
Example G: What colour jelly bean is that?
Do different coloured jelly beans taste the same? If they do, then for someone who is blindfolded and told that the jelly bean they are tasting could be any of 5 different colours, any of the colours are equally-likely to be chosen. The taste tester has a chance of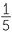 
or 20% of picking the correct colour.
Effects of assumptions of equally-likely probabilities
Already in earlier years, the assumption of equally-likely probabilities has been extended to simple cases where probabilities are assumed to be given by the relative number of outcomes or the relative sizes of outcomes.
For example, if a spinner has three segments equal and the fourth segment is twice the area of each of the other three, then the natural assumption is that the fourth segment is twice as likely as each of the other three. This is just the extension of assuming that equal areas are equally-likely because that assumption is essentially that the chance of the spinner landing on a segment is given by the relative size of the segment.
Similarly if we have a box of sweets with 8 red, 4 blue, 4 green and 4 yellow, then assuming that we are twice as likely to get a red sweet as blue is the natural extension of assuming we are equally-likely to get each of the 4 colours if there are equal numbers of sweets in the box. We are assuming that the probability of red is given by the number of red sweets/total number of sweets.
This is formalised and generalised in Year 8, but because in simple cases of number or size of outcomes, it is based on, and a natural extension of, assumptions of equally-likely probabilities, using it enables probabilities to be assigned to simple events based on the assumption of equally-likely outcomes.
Example A: Throwing one die
If a 6-sided die is fair and is well shaken in some container before throwing it, we can assume equally-likely probabilities for the 6 face values. Hence each face value has a chance of 
of appearing on one throw of a die.
What is the chance of an odd number? There are 3 possibilities, so the assumption of equally-likely face values extends to assuming that probabilities are given by the relative number of outcomes. There are 3 odd numbers in a total of 6 face values (1 to 6), so the probability of an odd number is 
= 
.
Example B: Throwing two dice
If both six-sided dice are fair and they are well shaken in a container before throwing, there is no reason not to assume that each of the above 36 outcomes is equally-likely. So we would assume that all of the ordered pairs of numbers are equally-likely when we throw two fair, differently coloured dice − or fair dice which can be distinguished in some way.
So the chance of getting each pair as listed above is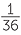 
. For example, the chance of getting two 6’s is 
.
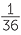Some board games use the sum of the faces of two dice to decide moves. What are the possible sums? Any of the numbers from 2 to 12 are possible. What is the chance of getting 12? It is the chance of getting two 6’s which is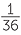 
. What is the chance of getting 11? There are two ways of getting 11; we could get a 5 on red & a 6 on blue or a 6 on red and a 5 on blue. So the chance of a sum of 11 is 
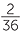. Similarly, the number of ways of getting a sum of 10 is 3: (4, 6), (5, 5), (6, 4). So the chance of getting a sum of 10 is 
.
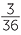Does anything change if the two dice look exactly the same? Even though they might look identical to us, they’re not exactly identical, and we still need to talk about what the first die gives and what the second die gives. There are still 36 equally-likely ordered pairs of numbers (provided the dice are fair and are shaken well before throwing), and the chances of getting the various sums are still the same.
Example C: What is the chance the winning ticket is one that you sold?
Raffles are usually run by people buying numbered (and sometimes coloured) tickets with the tickets being in two parts. The buyers keep one part and the other parts (we’ll call them the ticket stubs) are put into a container with someone picking out a ticket at random from the container. The outcomes of the draw are all the tickets that have been sold.
Often different coloured books of tickets are used, so that the winning ticket might be called out as “blue, number 16”. Suppose there are 5 ticket-sellers and each one has a book of 100 tickets and each book is a different colour. You are a seller and your book is green. All the tickets are sold. The stubs are put in a container and mixed well, and a guest pulls one out (without looking of course!). So there are 500 ticket stubs in the container and they are all equally-likely to be drawn. You sold 100 of these. So there’s a chance of 
= 0.2 that the winning ticket will be one that you sold.
Example D: How good are people at choosing numbers
at random?
A teacher asks each student in a class to choose a number at random from the numbers 1 to 50. If students are able to choose at random, then for each student, each number is equally-likely to be chosen. So each number has a chance of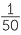 
or a 2% chance of being chosen.
How good is your class at choosing random numbers? Ask each student to write down 5 random numbers from 1 to 50 and then put them altogether. Use a dotplot to look at the results. You need a lot of people to be able to compare the relative frequencies of each of 50 numbers with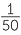 
, but you can compare the relative frequencies of groups of numbers with their chances if the numbers are random. For a random number from 1 to 50, what is the chance it’s in the group 1, 2, …10? 11, 12, …., 20? Each of these have 10 possible numbers, so the chance of falling into either of these groups if a number from 1 to 50 is chosen at random is 
= 
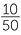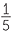= 0.2.
Example E: Which destination will the contestant win for a holiday?
In a TV contest, a contestant wins a holiday in Australia.
Now suppose that instead of 10 destinations behind doors, the contestant is blindfolded and places a pin on a board with Australian regions randomly placed on the map but with different areas of the board assigned to different regions. If the regions and their areas on the board are as follows, what is the chance the contestant will win a holiday in Queensland?
Queensland: 12cm2
NSW: 8cm2
Vic: 4cm2
SA: 8cm2
WA: 16cm2
Tas: 2cm2
NT: 9cm2
ACT: 1cm2
The total area of the board is 60cm2. If you put a pin in a board at random, what will be equally-likely? All the regions with an area of 1cm2 will be equally-likely. Hence the chance of putting the pin into the region of the board representing Queensland is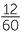 
= 
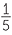= 0.2.
Example G: A taste testing experiment: what colour jelly bean is that?
Do different coloured jelly beans taste the same? If they do, then for someone who is blindfolded and told that the jelly bean they are tasting could be any of 5 different colours, any of the colours are equally-likely to be chosen. The taste tester has a chance of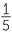 
or 20% of picking the correct colour.
To conduct a taste testing experiment with jelly beans, three different coloured jelly beans could be chosen, for example, red, green and white. The students know that these are the three colours. Each student is blindfolded in turn and given a jelly bean with its colour randomly-chosen from these three. To ensure the colour is randomly-chosen, a fair die could be tossed, with its six possible face values divided into three groups of two each, with each group corresponding to one of the three colours.
The interest in the data is comparisons between observed and expected frequencies (between relative frequencies and probabilities), remembering that even if probabilities are correct, there will be variation in observed frequencies (as experienced in Year 6 learning activities). There are a number of ways of investigating such data and also in setting up a taste testing experiment. For example, if 60 students take part in the taste testing experiment described above, the frequency of correct guesses can be compared with 20.
Another way of conducting a taste testing experiment is to give each participant two colours (say, red and green) in random order and ask them to say which one is red. The order can again be decided by tossing a fair die with three of its faces allocated to red and the others to green. If it’s not possible to distinguish between red and green by taste, the chance of being correct is 
or 50%.
There is a well-known story of a taste experiment conducted by the famous statistician
Sir Ronald Fisher, and often referred to as the lady tasting tea. The lady in question claimed to be able to tell whether the tea or the milk was added first to a cup. Fisher proposed to give her eight cups, four of each variety, in random order. One could then ask what the probability was for her getting the number she got correct, but just by chance.
In the design of experiments in statistics, this is a famous randomized experiment devised by Fisher and reported in his book Statistical methods for research workers. The lady in question was Muriel Bristol, and the test used was Fisher’s exact test. Sir Ronald’s experiment to test this claim at a tea party was so famous, that it was used as part of the title of a general book. The Lady Tasting Tea: How Statistics Revolutionized Science in the Twentieth Century (ISBN 0-8050-7134-2) is a book by David Salsburg about the history of modern statistics and the role statistics has played in the development of science and industry.
A quote from the publisher of this book is as follows:
At a summer tea party in Cambridge, England, a lady states that tea poured into milk tastes differently than that of milk poured into tea. Her notion is shouted down by the scientific minds of the group. But one guest, by the name Ronald Aylmer Fisher, proposes to scientifically test the lady’s hypothesis. There was no better person to conduct such a test, for Fisher had brought to the field of statistics an emphasis on controlling the methods for obtaining data and the importance of interpretation. He knew that how the data was gathered and applied was as important as the data themselves.
Some general comments and links from F-7 and towards year 8
From Years 1-6, students have gradually developed understanding and familiarity with simple and familiar events involving chance, including possible outcomes and whether they are “likely”, “unlikely” with some being “certain” or “impossible”. They have seen variation in results of simple chance experiments. In Year 4, they have considered more carefully how to describe possible outcomes of simple situations involving games of chance or familiar everyday outcomes, and how the probabilities of possible outcomes could compare with each other. They have also considered simple everyday events that cannot happen together and, in comparison, some that can. In Year 5, consideration of the possible outcomes and of the circumstances of simple situations has lead to careful description of the events and assumptions that permit assigning probabilities, understanding what the values of these probabilities must be and representing these values using fractions.
In Year 6, decimals and percentages have been used along with fractions to describe probabilities to help increase the sense of the size of probabilities and the extent − or lack of it − of the chance of outcomes. Understanding of probability has been extended to considering the implications for observing data in situations involving chance. The values of probabilities tell us the chance of observing outcomes each time we take an observation, but not exactly what we are going to get. What can we expect to see in a set of observations? In Year 6 students have collected data and carried out simple simulations of data to experience the effects of chance on observations.
In Year 7, students have revisited simple situations with a clear and easily listed number of possible outcomes that can, or may, be assumed to be equally-likely. In these special, limited situations, they have considered probabilities of events by applying the concept of equal chances for equal “sizes” of events. For example, some are obtained as the number of equally-likely outcomes/total number of equally-likely outcomes, and some are obtained as area of region/total area. To link with Year 6 experiences, they have also collected data to compare observed frequencies with expected frequencies under the assumption of equally-likely probabilities.
In Year 8, students see some of the properties of probabilities they have been using in simple situations, and learn how to interpret some of the common elements of the language of describing events.
Note for teachers’ background information.
Much is written in educational literature about coin tosses and much has been tried to be researched and analysed in students’ thinking about coin tossing. This situation is far more difficult than is usually assumed in such research which often tends to take the assumptions of fair coins and independent tosses as absolutely immutable and not to be questioned. In addition a common mistake is to state that it demonstrates either poor or, in contradiction, good thinking, to say that a particular sequence of coin tosses with a mixture of heads and tails is more likely than a sequence of the same outcome, when in practice it is not made clear whether the researcher or the student is thinking of a particular ordered sequence or merely a mixture of heads and tails. For example, if a coin is fair and tosses are independent, the chance of HTHHTT is EXACTLY the same as the chance of HHHHHH, but many people think of the first outcome in terms of getting 3 H’s and 3 T’s which is not the same as getting a particular sequence with 3 H’s and 3 T’s.
With regard to the assumption of a fair coin and independent tosses, the assumptions are the same as tossing dice. However, it is more difficult in practice to toss a coin completely randomly than to toss dice randomly, and also to assume that a particular person does not tend to toss a coin in a similar manner each toss. It is also extremely difficult in practice to identify whether unlikely sequences are due to an unfair coin or how it is tossed, and it would be of far greater benefit in research, but far more challenging, to devise experiments in which these two assumptions could be separately investigated.
Indeed, if, on observing an unlikely sequence, students do question either the fairness of a coin or no connection between consecutive coin tosses, then are they not demonstrating intuitive understanding of statistical hypothesis testing? Note that there is a difference between observing a simulation and observing a real situation because assumptions are easier to accept in a simulation.
For some excellent comments on this, see the letter by Harvey Goldstein to the Editor of Teaching Statistics (2010), Volume 32, number 3.
Because of the over-emphasis in educational research on coin tossing, and the problems caused by lack of clarity and understanding in much written on this topic, examples using coin tossing are avoided as much as possible in these modules.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
