The Improving Mathematics Education in Schools (TIMES) Project
- Facility with basic algebra, particularly expanding brackets and collecting like terms.
- LCM and HCF for arithmetic.
Proficiency with algebra is an essential tool in understanding and being confident with mathematics. For those students who intend to study senior mathematics beyond the general level, factoring is an important skill that is frequently required for solving more difficult problems and in understanding mathematical concepts.
In arithmetic, finding the HCF or LCM of two numbers, which was used so often in working with fractions, percentages and ratios, involved knowing the factors of the numbers involved. Thus the factoring of numbers was very useful in solving a whole host of problems.
Similarly in algebra, factoring is a remarkably powerful tool, which is used at every level. It provides a standard method for solving quadratic equations as well, of course, as for simplifying complicated expressions. It is also useful when graphing functions.
Factoring (or factorising) is the opposite of expanding. Thus, using the distributive law,
3(x − 2) is the factored form of 3x − 6, and (x − 1)(x + 6) is the factored from x2 + 5x − 6.
While expanding is relatively routine, factoring can be tricky, and the student will need lots of practice to master the different types of factorisation that arise, as well as gain insight into what methods to apply and proficiency in applying them.
The simplest type of factoring involves taking out a common factor from two or more terms.
For example, each term in the expression 6x2y − 4x is divisible by 2 and by x. Thus, 2x is a common factor. Since there is no other common factor, 2x is the highest common factor. We divide each term by and see what is left. Thus,
![]() 6x2y − 4x = 2x(3xy − 2).
6x2y − 4x = 2x(3xy − 2).
The terms in the expression in the brackets have no common factor (except 1) and so this expression cannot be factorised further.
Removing common factors can also be performed on more than two terms.
Example
Factor 6a2b − 8ab + 10ab2.
Solution
The highest common factor of the three terms is 2ab so
6a2b − 8ab + 10ab2 = 2ab(3ab − 4 + 5b)
In some instances, there may be no common factor of all the terms in a given expression. It may, however, be useful to factor in pairs.
For example, there is no common factor of the four terms in the expression
![]() 2a2 + 3ab + 4 + 6b,
2a2 + 3ab + 4 + 6b,
however, the first two terms have a common factor of a while the second two have a common factor of 2. Thus,
![]() 2a2 + 3ab + 4a + 6b = a(2a + 3b) + 2(2a + 3b).
2a2 + 3ab + 4a + 6b = a(2a + 3b) + 2(2a + 3b).
We can now see that the two resulting terms have a common factor of that can now be factored out to produce (2a + 3b)(a + 2).
| Hence | |
2a2 + 3ab + 4a + 6b | = a(2a + 3b) + 2(2a + 3b) |
| = (2a + 3b)(a + 2). |
Note that the order in which the brackets are written and the order of the terms within the brackets do not matter.
Students will need some practice with this method, especially with the second step.
EXAMPLE
Factor 3a2 − 5ac − 3ab + 5cb.
Solution
| 3a2 − 5ac − 3ab + 5cb | = a(3a − 5c) − b(3a − 5c) | ||
| = a(3a − 5c) − b(3a − 5c) | (Note that we factor out to obtain the next common factor.) |
||
| = (3a − 5c)(a − b) | (Take out the common factor). |
Note: Different pairing of terms may or may not lead to a useful factorisation. Thus, in the above example, pairing up 3a2 − 5ac − 3ab + 5cb leads to 3a(a − b) − 5b(a − b) as before. However pairing the terms as (3a2 + 5cb) − 5ac − 3ab does not lead to a factorisation.
Factoring can give us useful information regarding an expression as the following
exercise shows.
EXERCISE 1
Factorise the expression xy − 5x − 2y + 10 and state conditions on x, y such that when numerical values are substituted for x and y the given expression
a![]() is equal to 0,
is equal to 0, ![]() b
b![]() is positive,
is positive, ![]() c
c![]() is negative.
is negative.
There are three special expansions and corresponding factorisations that frequently occur in algebra.
The first of these is an identity known as the difference of squares. An identity is a statement in algebra that is true for all values of the pronumerals.
By expanding, it is easy to show that
![]() (x − y)(x + y) = x2 − y2.
(x − y)(x + y) = x2 − y2.
Hence the difference between the squares of two numbers equals their sum times their difference.
EXAMPLE
Factor ![]() a
a![]() c2 − 25
c2 − 25 ![]() b
b![]() 16a2 − 9y2.
16a2 − 9y2.
Solution
a![]() c2 − 25 = (c − 5)(c + 5)
c2 − 25 = (c − 5)(c + 5) ![]() b
b![]() 16a2 − 9y2 = (4a + 3y)(4a − 3y)
16a2 − 9y2 = (4a + 3y)(4a − 3y)
(As usual, the order in which the factors are written is unimportant.)
This identity can be used to simplify algebraic expressions.
EXAMPLE
Simplify 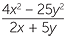 .
.
Solution
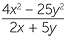 =
= 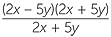 = 2x − 5y.
= 2x − 5y.
There are a number of useful applications of completing the square.
One such application is to mental arithmetic. For example, to multiply say 13 and 15,
we write the product as 13 × 15 = (14 − 1)(14 + 1) = 142 − 1 = 195.
With practice this can be done mentally, provided the squares of integers up to about
20 are known.
The difference of two squares can also be used to solve equations in which we only seek integer solutions.
EXAMPLE
Find all positive integer solutions to x2 − 9y2 = 13.
Solution
Factoring the left-hand side, we have (x − 3y)(x + 3y) = 13
Because x and y are positive, it follows that x + 3y and x − 3y hence are positive since their product is 13.
The only positive factors of 13 are 13 and 1, so we have the two cases:
|
(x − 3y) = 1 and (x + 3y) = 13 Adding gives so 2x = 14 so x = 7. Substituting back we obtain y = 2. |
(x − 3y) = 13 and (x + 3y) = 1 Adding gives so 2x = 14 so x = 7. Substituting back we obtain y = −2. |
Since we only want positive integer solutions, we conclude that the only positive integer solution to x2 − 9y2 = 13 is x = 7, y = 2.
The other two special expansions referred to above are the identities:
![]() a2 + 2ab + b2 = (a + b)2 and a2 − 2ab + b2 = (a − b)2.
a2 + 2ab + b2 = (a + b)2 and a2 − 2ab + b2 = (a − b)2.
These identities are harder to use than the difference of two squares and are probably
best dealt with as special cases of quadratic factoring, discussed below. Thus, for example, it is not easy for students to quickly spot that 4x2 − 12xy + 9y2 is a perfect square equal to (2x − 3y)2.
The following example shows how these ideas can be cleverly combined to factor an expression that at first glance does not appear to factor.
Recognising simple examples of perfect squares is a useful skill.
EXAMPLE
Factor x4 + 4.
Solution
At first glance this expression does not appear to factor, since there is no identity for the sum of squares.
However, by adding and subtracting the term , we arrive at a difference of squares.
| x4 + 4 | = (x4 + 4x2 + 4) − 4x2 | |
| = (x2 + 2)2 − (2x)2 |
||
| = ((x2 + 2) − 2x)((x2 + 2) − 2x) | ||
| = (x2 − 2x + 2)(x2 + 2x + 2) |
A monic quadratic is an expression of the form x2 + bx + c, where and are given numbers.
When we expand, for example, (x + 2)(x + 5), we obtain
| (x + 2)(x + 5) | = x(x + 5) + 2(x + 5) | |
| = x2 + 5x + 2x + 10 | ||
| = x2 + 7x + 10. |
This expansion produces a simple quadratic. We would like to find a procedure that reverses this process.
We notice that the coefficient x of is the sum of the two numbers 2 and 5 in the brackets and that the constant term 10, is the product of 2 and 5. This suggests a method of factoring.
In general, when we expand (x + α)(x + β), we obtain
![]() (x + α)(x + β) = x2 +αx + βx + αβ = x2 + (α + β)x + αβ.
(x + α)(x + β) = x2 +αx + βx + αβ = x2 + (α + β)x + αβ.
The coefficient of x is α + β and the constant term is αβ. Hence to reverse the process, we seek two numbers whose sum is the coefficient of and whose produce is the constant term.
EXAMPLE
Factor x2 + 7x + 12.
Solution
We seek to express this in the form (x + α)(x + β). To find the values of a and b, we solve, by inspection, α + β = 7 and αβ = 12. Clearly the solutions are 4 and 3 (in either order), and no other numbers satisfy these equations. Hence
![]() x2 + 7x + 12 = (x + 4)(x + 3).
x2 + 7x + 12 = (x + 4)(x + 3).
Note that the order in which we write the brackets is unimportant.
Students should try to mentally expand to check that their answers are correct.
EXAMPLE
Factor a![]() x2 − 7x + 12
x2 − 7x + 12![]() b
b![]() x2 + 2x − 15
x2 + 2x − 15![]() c
c![]() x2 + 6x + 9
x2 + 6x + 9
Solution
- a
- We solve, by inspection, α + β = −7 and αβ = 12.
The solutions are −4 and −3. Hence
x2 − 7x + 12 = (x − 4)(x − 3). - b
- We solve, by inspection, α + β = 2 and αβ = −15. The solutions are 5 and −3. Hence
x2 + 2x − 15 = (x + 5)(x − 3).
- c
- We solve, by inspection, α + β = 6 and αβ = 9. The solutions are 3 and 3. Hence
x2 + 6x + 9 = (x + 3)(x + 3) = (x + 3)2.
Note that in c the answer is a perfect square.
Also note that the difference of squares factorisation could also be done using this method. For example, to factor x2 − 16, we solve α + β = 0 and αβ = −16. The solutions are 4 and −4 work, so x2 − 16 = (x − 4)(x + 4).
This is, however, not a good method to use. It is better for students to be on the look out for the difference of squares identity and apply it directly.
Students will need a lot of practice with factoring quadratics. It is worth mentioning here that in further mathematics, both in the senior years and all the way through tertiary level mathematics, quadratic expressions routinely appear and so being able to quickly factor them is a basic skill.
Quadratics with common factors
We should always be on the look out for common factors before using other
factoring techniques.
For example, to factor 3x2 + 9x + 6, we begin by taking out the common factor 3. We can then proceed to factor further. Thus,
| 3x2 + 9x + 6 | = 3(x2 + 3x + 2) | |
| = 3(x + 2)(x + 1) |
EXERCISE 2
Factor 6x2 − 54.
We said above that a monic quadratic is an expression of the form x2 + bx + c,
where b and c are given numbers. A non-monic quadratic is an expression of the form ax2 + bx + c, where a, b and c are given numbers, and a ≠ 1 or 0.
Thus, for example, 2x2 + 5x + 3 is an example of a non-monic quadratic.
There are a number of different techniques for factoring this type of expression. The one presented here is felt to be the easiest both to perform and explain. It also links in with the techniques discussed above. There are three steps in the method, which will be illustrated on the example 2x2 + 5x + 3.
- Step 1
- Multiply the coefficient of by the constant term and write this above the constant term
| 6 | ||
| 2x2 + 5x+ | 3 |
- Step 2
- Find two numbers that add to give the coefficient of and multiply to give this new product. That is, two numbers that add to give 5 and multiply to give 6. The numbers 3 and 2 work.
- Step 3
- Use these numbers to split the middle term and factor in pairs.
| 2x2 + 5x + 3 | = 2x2 + 2x + 3x + 3 | |
| = 2x(x + 1) + 3(x + 1) | ||
| = (x + 1)(2x + 3). |
These steps are precisely the reverse process of expanding.
It does not matter in what order we write the middle terms, the method will still work, thus
| 2x2 + 5x + 3 | = 2x2 + 3x + 2x + 3 | |
| = x(2x + 3) + 1(2x + 3) | ||
| = (x + 1)(2x + 3). |
EXAMPLE
Factor 3x2 + 5x − 2.
Solution
| 3x2 + 5x − 2 | (3 × (−2 )= −6) | |||
| 3x2 + 5x − 2 | = 3x2 + 6x − x −2 | |||
| = 3x(x + 2) −(x + 2) | (6 − 1 = 5, 6 × (−1) = −6) | |||
| = 3x(x + 2) −1(x + 2) | ||||
| = (x + 2)(3x − 1) |
Given an expression with two terms:
- look for a common factor
- look for a difference of squares
Given an expression with three terms:
- look for a common factor
- factor using the method for monic quadratics
- factor using the method for non-monic quadratics
Given an expression with four terms:
- look for a common factor
- try grouping in pairs.
Simplifying algebraic expressions
We will now apply the various techniques of factoring to simplify various algebraic expressions. Students must take great care when cancelling. False cancellations such as 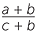 =
= 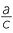 are common student errors when dealing with algebraic fractions. They must not confuse this with the cancellation
are common student errors when dealing with algebraic fractions. They must not confuse this with the cancellation 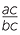 =
=  .
.
EXAMPLE
Simplify
a![]()
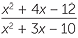
![]() b
b![]()
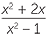 ×
× 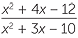
![]() c
c![]()
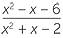 ÷
÷ 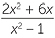
Solution
| a | 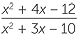 |
= 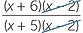 |
|
= 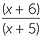 |
| b | 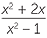 × × 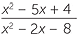 |
= 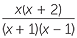 × × 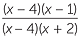 |
|
= 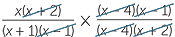 |
|||
= 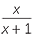 |
| c | Invert and multiply before factorising. | ||
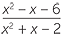 ÷ ÷ 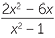 |
= 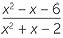 × × 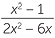 |
||
= 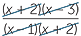 × × 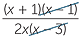 |
|||
= 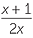 |
|||
Factorising also can assist us in finding the lowest common denominator when adding or subtracting algebraic fractions.
EXAMPLE
Simplify 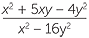 −
− 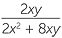 .
.
Solution
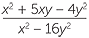 − − 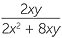 |
= 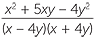 − − 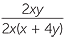 |
= 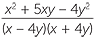 − − 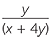 |
|
= 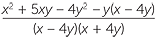 |
|
= 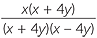 |
|
= 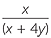 . . |
Factoring quadratics provides one of the key methods for solving quadratic equations. Equations such as these arise naturally and frequently in almost every area of mathematics.
The method of solution rests on the simple fact that if we obtain zero as the product of two numbers then at least one of the numbers must be zero.
That is, if ab = 0 then a = 0 or b = 0.
Hence to solve x2 − 7x + 12 = 0, we factor the quadratic as (x − 4)(x − 3) = 0 and conclude that either (x − 4) = 0 or (x − 3) = 0.
These equations can be easily solved to give x = 3 or x = 4.
The method of factoring non-monic quadratics can similarly be used to solve non-monic quadratic equations.
EXAMPLE
Solve 3x2 + 5x − 2 = 0.
Solution
3x2 + 5x − 2 = 0
(3x − 1)(x + 2) = 0
3x − 1 = 0 or x + 2 = 0
So, x = 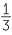 or x = −2.
or x = −2.
It will be noted that not all quadratic equations have rational solutions. These equations are not amenable to the factoring method.
Other techniques will be developed in the module Quadratic Equations to handle
such equations.
The difference of squares identity discussed above can be generalised to cubes.
By expanding the right-hand side, we can show that
a3 − b3 = (a − b)(a2 + ab + b2) ![]() and
and![]() a3 + b3 = (a + b)(a2 − ab + b2).
a3 + b3 = (a + b)(a2 − ab + b2).
These identities are called the difference of cubes and sum of cubes respectively. In both cases, the factor in the second bracket can be remembered as `square the first, square the second, multiply and change the sign’.
These identities are generally covered in senior mathematics and are useful in beginning calculus and for finding limits.
The difference of squares and the difference of cubes can be further generalised to obtain a factorization of an − bn.
By expanding the right-hand side, we can show that
![]() an − bn = (a − b)(an−1 + an−2b + an−3b2 + … + abn−2 + bn−1)
an − bn = (a − b)(an−1 + an−2b + an−3b2 + … + abn−2 + bn−1)
As a special case of this, we note that
![]() xn − 1 = (x − 1)(xn−1 + xn−2 + xn−3 + … + x + 1).
xn − 1 = (x − 1)(xn−1 + xn−2 + xn−3 + … + x + 1).
Exercise 3
- a
- By expanding, check each of these identities.
- b
- Verify that we obtain the difference and squares and cubes, when we replace
n with 2 and 3. - c
- Factor x4 − 1 both by using the above identity and also by using the difference of squares. Compare the two factorisations.
While there is no ‘sum of squares’, the sum of cubes does admit generalisation.
If we use odd indices, we find that
x5 + 1 = (x + 1)(x4 − x3 + x2 − x + 1) and
x7 + 1 = (x + 1)(x6 − x5 + x4 − x3 + x2 − x + 1), and so on.
EXERCISE 4
Write down and check by expansion, the factorisation of x2n+1 + 1.
Expressions such as x3 − 6x2 + 3x − 1 are called polynomials. Since the highest power of x in the expression is 3, we call this a polynomial of degree 3, or a cubic. Polynomials will be discussed further in the module Polynomials.
There are methods of factoring such expressions. Sometimes it is impossible to factor polynomial into linear factors using rational numbers, but it may be possible to factor an expression containing terms with degree 6 say into a product containing terms with x3. For example, x6 − x4 + 2x3 − 2x + 2 can, with some difficulty, be factored as (x3 + 2)(x3 − x + 1). The expressions in each bracket cannot be further factored using only rational numbers. We say that these factors are irreducible over the rational numbers.
There are expressions that are irreducible over the rational numbers, but which can be factored if we allow irrational numbers. For example, the polynomial x4 + 1 cannot be factored using rational numbers, but it can factored using a method similar to that given on page 5 as (x2 + ![]() x + 1)(x2 −
x + 1)(x2 − ![]() x + 1). This can be verified by expansion. We call this a factorisation over the real numbers.
x + 1). This can be verified by expansion. We call this a factorisation over the real numbers.
Students who go on to study complex numbers in senior mathematics will discover that:
- over the complex numbers every polynomial can be factored into a product of linear factors,
- over the real numbers every polynomial can be factored into a product of linear and/or quadratic factors.
Over the rational numbers, it is possible to find polynomials, with degree as large as we like, that are irreducible. For example, x6 + x5 + x4 + x3 + x2 + x + 1 can be shown to be irreducible over the rational numbers.
Factoring is a part of algebra and so its history belongs to the history of algebra covered in other modules.
Questions of factoring and developing methods of factoring, at a more advanced level, were part of the work of great mathematicians such as Gauss (1777-1855), Galois (1811-1832) and Abel (1802-1829). It was Gauss who first gave a proof that polynomials can be completely factored into linear factors over the complex numbers.
Polynomials that arise from factoring xn − 1 over the integers are called cyclotomic polynomials and were also studied by these and later mathematicians. For example, since x3 − 1 = (x − 1)(x2 + x + 1) the polynomial x2 + x + 1 is an example of a cyclotomic polynomial. These polynomials have interesting properties and there are a number of unsolved problems regarding them.
One of the many applications of factoring, that goes back to the Greeks, is the solution of equations in which we seek only integer (sometimes positive integer) solutions. Such equations are called Diophantine equations. These sometimes use clever factorisations.
EXAMPLE
Find all positive integer solutions to ab + 2a + 5b = 38.
Solution
The first two terms factor as a(b + 2). We add 10 to both sides, so that we can factor in pairs. Thus,
| ab + 2a + 5b | = 38 | |
| ab + 2a + 5b + 10 | = 48 | |
| a(b + 2) + 5(b + 2) | = 48 | |
| (a + 5)(b + 2) | = 48 |
Equating each bracket with a factor and cofactor 48 and solving, we find that the only positive integer solutions are a = 11, b = 1; a = 1, b = 6; a = 3, b = 4; a = 7, b = 2.
EXERCISE 5
Check all the steps in the above example and then also find all the integer solutions.
EXERCISE 1
a![]() x = 2 or y = 5
x = 2 or y = 5 ![]() b
b![]() x > 2 and y > 5 or x < 2 and y < 5
x > 2 and y > 5 or x < 2 and y < 5
c![]() x > 2 and y < 5 or x < 2 and y > 5
x > 2 and y < 5 or x < 2 and y > 5
EXERCISE 2
6(x − 3)(x + 3)
EXERCISE 4
x2n + 1 + 1 = (x + 1)(x2n − x2n−1 + x2n … + x2 − x + 1)
EXERCISE 5
a = −17, b = − 6; a = −9, b = − 14; a = −8, b = − 18; a = −21, b = − 5; a = −7, b = − 26;
a = −29, b = − 4; a = −11, b = − 10; a = −13, b = − 8; a = −6, b = − 50; a = −4, b = − 46;
a = 43, b = − 1; a = − 3, b = 22; a =19, b = 0; a = −1, b = 10; a = 7, b = 2; a = −2, b = 14.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

