Year 9

The word 'similar' is used frequently, meaning like something else. For example, some sisters are said to be similar in appearance, the weather today is similar to that of yesterday and the music of Beethoven is not similar to that of Mozart.

When objects or shapes are said to be similar in mathematics, something quite specific is implied. One object is similar to another if the proportions are the same, which means one object is a scaled version of the other just as in architects' drawings and maps.

Detailed description

Scale drawings are used when we increase or reduce the size of an object so that it fits nicely on a page or computer screen. For example, we want to reduce the size when drawing:

• the plan of the facade of a building
• a map of a suburb or a country
• a photograph of a distant galaxy

and we want to increase the size when drawing:

• a diagram of a printed circuit
• a magnified photograph of an insect
• a drawing of a human cell.

The proportional increase or decrease in lengths is called the scale of the drawing. It is usually expressed in terms of a ratio, so the topic of scale drawings is closely related to ratios and fractions.

The transformation that produces a scale drawing is an enlargement. An enlargement transformation preserves the shape of the figure but increases or decreases all distances by a constant ratio.

This is different from the three transformations that we have already introduced − translations, rotations and reflections all produce an image that is the same size and shape as the original figure.

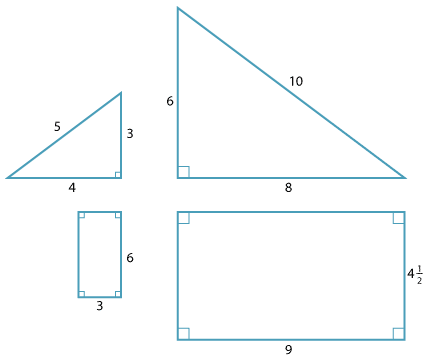
Congruent figures are figures that can be mapped one to the other by a sequence of translations, rotations and reflections. Figures that can be mapped one to the other by these transformations and enlargements are called similar. Thus, two figures are similar if an enlargement of one is congruent to the other figure, as in the following examples:

Detailed description

The theory of similarity develops in the same way as the theory of congruence. First, most situations involving similarity can be reduced to similar triangles. There are four standard similarity tests for triangles, corresponding to the four congruence tests for triangles.