The Improving Mathematics Education in Schools (TIMES) Project
- Introductory plane geometry involving points and lines, parallel lines and transversals, angle sums of triangles and quadrilaterals, and general angle-chasing.
- Introduction to logical arguments in geometry written as a sequence of steps, each justified by a reason.
- Informal experience with translations, reflections and rotations, and with the symmetries associated with them.
- Familiarity with ruler-and-compasses constructions and Pythagoras' theorem.
Two geometric figures may resemble each other in some ways, but differ in others. For example, all the angles of the square and the rectangle below are right angles, and they have the same area, but their side lengths are different.

On the other hand, the two figures below are exactly the same in all respects apart from their position and orientation − we can pick up one of them and place it so that it fits exactly on top of the other. Such figures are called congruent.
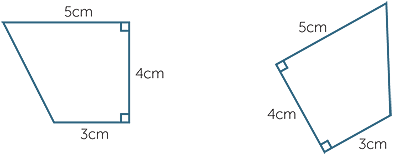
Knowing that two figures are congruent is important. For example, if we measure or calculate the unmarked side length of the diagram on the left above, then the matching length is the same in the diagram on the right above. (Pythagoras’ theorem gives us the answer 2![]() cm for this length.) This very simple idea of matching lengths, matching angles, and matching areas becomes the means by which we can prove many geometric results.
cm for this length.) This very simple idea of matching lengths, matching angles, and matching areas becomes the means by which we can prove many geometric results.
A polygon can always be divided up into triangles, so that arguments about the congruence of polygons can almost always be reduced to arguments about congruent triangles. Most of our discussion therefore concerns congruent triangles. We shall develop the four standard tests used to check that two triangles are congruent. It is also true that figures involving curves can be congruent, such as circles of the same radius.
A good way to think about congruence is to ask, ‘How much information do I need to give someone about a figure if they are going to draw it?’ For example, surveyors go to a lot of trouble taking careful measurements of a landscape. They must know that everything important about that landscape can be calculated from the measurements that they have taken. In an analogous way, a certain minimum amount of information is needed to draw a particular triangle. We will develop the congruence tests as a solution to this question.
A great deal of mathematics depends on finding and exploiting symmetries. This is particularly true in geometry, where the elementary figures that we study —like squares, rectangles, circles − exhibit obvious reflection and rotation symmetries. Argument based on direct appeals to symmetry, however, is notoriously difficult to construct and to evaluate, and the ancient Greek mathematicians, most famously Euclid, introduced argument based on congruence as a replacement. The resulting geometric proofs, using mostly only congruent triangles, are clear and straightforward in their logic.
Justifying the congruence tests is no easy matter − the logical problems inherent in them were only sorted out at the end of the nineteenth century, by David Hilbert in particular. We will take the first three tests as axioms of our geometry, and will be content to demonstrate their reasonableness using ruler-and compasses constructions.
If we take the five of spades from each of two identical decks of cards, they look exactly the same. We can move one card and place it on top of the other one so that the pictures on the two cards coincide exactly, as shown below.
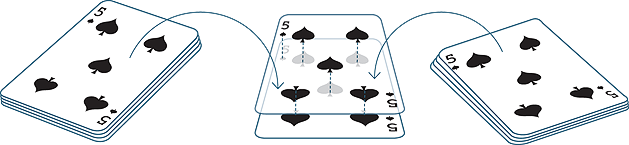
Two objects like this are called congruent. The word ‘congruent’ comes from Latin and means ‘in agreement’ or ‘in harmony’.
Definition: Two plane figures are called congruent if one figure can be moved so that it fits exactly on top of the other figure.
If two figures are congruent, such a movement can always be done by a sequence of translations, rotations and reflections − reflect the first figure in any axis if it has the opposite parity to the second, then translate any point of the first figure to the matching point of the second figure, then rotate the first figure until it fits exactly on top of the second. Thus congruent figures can be defined in an alternative way that specifies the allowed transformations:
 ‘Two plane figures are called congruent if
‘Two plane figures are called congruent if
one can be moved by a sequence of translations,
rotations and reflections so that it fits exactly
on top of the other figure.’
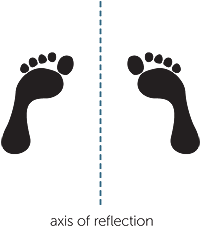
The example above with the cards involved translations
and rotations. In the diagram to the right, the two footprints
are congruent because one can be reflected onto the other.
Matching up the parts of congruent figures
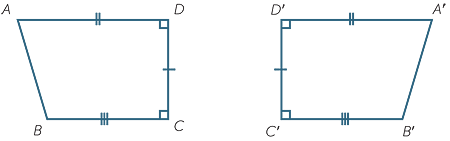
When two figures are congruent, we can match every part of one figure with the corresponding part of the other figure. For example, the two figures below are congruent.
Some of the matchings of points with points, intervals with intervals, and angles with angles are:
![]() A
A  A′
A′ ![]()
![]() AB
AB  A′B′
A′B′![]()
![]()
 BAD
BAD 
 B′A′D′
B′A′D′
Matching intervals have the same length, and matching angles have the same size.
ABCD and A′B′C′D′ have the same area.
Congruent figures
- Two plane figures are called congruent if one figure can be moved so that it fits
exactly on top of the other figure. - This movement can always be effected by a sequence of translations, rotations
and reflections. - Congruent figures have exactly the same shape and size, each part of one figure can be matched with a part of the other figure, and
- matching angles have the same size,
- matching intervals have the same length,
- matching regions have the same area.
When geometric figures are made up entirely of intervals, rather than curves, arguments about congruence can usually be reduced to arguments about congruent triangles. This is one reason why so much attention is given to congruent triangles.
Here are two congruent triangles. The triangle PQR on the right has been formed by a translation of the triangle ABC on the left.
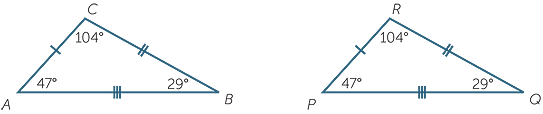
The vertices and sides of triangle ABC are matched by the congruence with the vertices and sides of triangle PQR as follows:
A P P |
B  Q Q |
C  R R |
||||
BC  QR QR |
CA  RP RP |
AB  PQ PQ |
All this can be expressed extremely concisely by using the symbol  for ‘is congruent to’, and by observing the convention that the two triangles are named with the vertices in matching order:
for ‘is congruent to’, and by observing the convention that the two triangles are named with the vertices in matching order:
![]()
 ABC
ABC 
 PQR
PQR
Congruence statements
When we write a congruence statement, we always write the vertices of the two congruent triangles so that matched vertices and sides can be read off in the natural way. For example, the statement  ABC
ABC 
 PQR means that:
PQR means that:
AB = PQ, BC = QR, CA = RP, and  A =
A =  P,
P,  B =
B =  Q,
Q,  C =
C = R.
R.
The four standard congruence tests
There are four standard congruence tests for two triangles to be congruent. These notes will introduce and discuss them one by one, but they, and their standard initials, are summarised here at the start to indicate the structure of the following discussion:
The four standard congruence tests for triangles
Two triangles are congruent if:
SSS: the three sides of one triangle are respectively equal to the three sides of the other triangle, or
SAS: two sides and the included angle of one triangle are respectively equal to two sides and the included angle of the other triangle, or
AAS: two angles and one side of one triangle are respectively equal to two angles and the matching side of the other triangle, or
RHS: the hypotenuse and one side of one right-angled triangle are respectively equal to the hypotenuse and one side of the other right-angled triangle.
Each congruence test will be justified by finding out what is a minimal amount of information − in terms of side lengths and angle sizes − needed to construct a triangle that is unique up to congruence, meaning that any two such triangles are congruent.
The SSS congruence test
Suppose first that we are asked to construct a triangle ABC in which
AB = 12cm and AC = 5cm
There are infinitely many ways to do this, because the two sides can remain joined at A, but flap around. Three such triangles are shown below, and they are clearly not congruent.
This shows that just knowing that two pairs of sides are equal is not enough information to establish congruence.

Constructing a triangle with three given sides
When all three sides of a triangle are given, however, there is no longer any freedom of movement, and only one such triangle can be constructed (up to congruence). To demonstrate this, suppose that we are asked to construct a triangle ABC with three given sides lengths:
AB = 12cm BC = 10cm CA = 5cm
In the module, Constructions we have seen that we can carry out this construction using ruler and compasses, as in the diagram below.
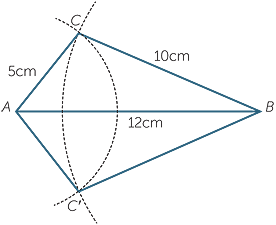
This construction has yielded two triangles with the given measurements. However, these two triangles, are congruent. This is because if we reflect the whole diagram in the line AB, then each circle falls exactly on itself, so the reflection of the intersection point C must be the other intersection point C′.
This establishes that it is reasonable to take the SSS congruence test as an axiom
of geometry.
SSS congruence test
- If the three sides of one triangle are respectively equal to the three sides of another, then the two triangles are congruent.
- If we are given the lengths of the three sides of a triangle, then only one such triangle can be constructed (up to congruence).
The initials SSS stand for ‘Side’, ‘Side’, ‘Side’.
Notice that this congruence test tells us that the three angles of a triangle are completely determined by its three sides. After trigonometry has been introduced, the cosine rule can be used to find the sizes of these angles.
EXERCISE 1
The second dotpoint in the box above does not imply that given any three lengths, a triangle can be constructed with those lengths as side lengths. What restriction must be placed on the three side lengths in order for a triangle with those side lengths to exist?
The example below shows that a quadrilateral with opposite sides equal is a parallelogram. Many results of this type will be discussed in the module, Parallelograms and Rectangles.
EXAMPLE
In the diagram to the right, the opposite sides of the quadrilateral
ABCD are equal, and the diagonal BD has been drawn.
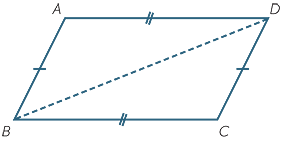 a Prove that
a Prove that  ABD
ABD 
 CDB.
CDB.
b Prove that AB || DC and AD || BC.
Solution
a In the triangles ABD and CDB:
1 AD = CB (given)
2 AB = CD (given)
3 BD = DB (common)
so  ABD
ABD 
 CDB (SSS).
CDB (SSS).
b Hence  ABD =
ABD =  CDB (matching angles of congruent triangles)
CDB (matching angles of congruent triangles)
so AB || DC (alternate angles are equal)
and  ADB =
ADB =  CBD (matching angles of congruent triangles)
CBD (matching angles of congruent triangles)
so AD || BC (alternate angles are equal).
Using congruence to prove the validity of constructions
We claimed in the module, Constructions that the validity of the ruler-and-compasses constructions described there could be established once congruence had been introduced. The following exercises proves that two of the constructions work.
EXERCISE 2
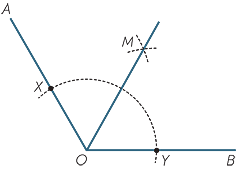 This exercise proves the validity of the standard construction to bisect a given angle.
This exercise proves the validity of the standard construction to bisect a given angle.
The diagram to the right shows an angle  AOB .
AOB .
A circle with centre O cuts the arms at X and Y, and circles with centres X and Y and the same radius meet at M .
Use the SSS congruence test to prove that OM bisects  AOB .
AOB .
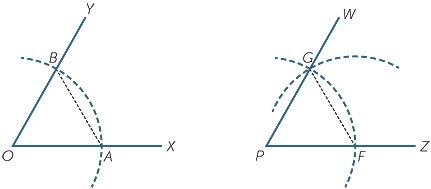
EXERCISE 3
This exercise proves the validity of the standard construction to copy a given angle.
The diagram below shows a given angle  XOY , and an interval PZ. A circle with centre O is drawn cutting the arms at A and B, and a second circle with the same radius is drawn with centre P cutting PZ at F . A circle with centre F and radius AB is drawn, cutting the second circle at G. Use congruence to prove that
XOY , and an interval PZ. A circle with centre O is drawn cutting the arms at A and B, and a second circle with the same radius is drawn with centre P cutting PZ at F . A circle with centre F and radius AB is drawn, cutting the second circle at G. Use congruence to prove that  ZPW has the same size as
ZPW has the same size as  XOY.
XOY.
The SAS congruence test
The three triangles on page 6 showed that when only two sides of a triangle are specified, there is nothing to stop those two sides ‘flapping about’. The other way to stop the two sides flapping is to specify the angle between them. This angle between the sides is called the included angle. The included angle can be any angle between 0° and 180°.
Constructing a triangle given two sides and the included angle
To illustrate this, let us construct a triangle ABC in which
AB = 4cm BC = 6cm  B = 30° (This is the included angle.)
B = 30° (This is the included angle.)
Draw lines BA and BA'
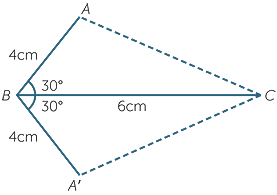
The two triangles ABC and A′BC are congruent, because triangle ABC falls exactly on triangle A'BC when it is reflected in the line BC.
This establishes that it is reasonable to take the SAS congruence test as an axiom
of geometry.
The SAS congruence test
- If two sides and an include angle of one triangle are respectively equal to two sides and the included angle of another triangle, then the triangles are congruent.
- If we are given the lengths of two sides of a triangle and the size of the included angle, then only one such triangle can be constructed (up to congruence).
The initials SAS stand for ‘Side’, ‘Angle’, ‘Side’.
The included angle can be any angle strictly between 0° and 180°. This congruence test tells us that the sides and angles of a triangle are completely determined by any two of its sides and the angle included between them. The cosine rule can be used to find the length of the third side and the sizes of the other two angles.
EXAMPLE
This example demonstrates a method of constructing a parallelogram from the diameters of two concentric circles.
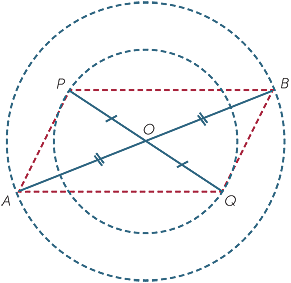
The intervals AOB and POQ are diameters of two concentric circles with centre O.
a Prove that  AOP
AOP 
 BOQ and hence prove AP || QB.
BOQ and hence prove AP || QB.
b Prove that  POB
POB 
 QOA and hence prove PB || AQ. Conclude that APBQ is a parallelogram.
QOA and hence prove PB || AQ. Conclude that APBQ is a parallelogram.
Solution
a In the triangles  AOP and
AOP and  BOQ:
BOQ:
AO = BO (radii)
PO = QO (radii)
 AOP =
AOP =  BOQ (vertically opposite angles)
BOQ (vertically opposite angles)
so  AOP
AOP 
 BOQ (SAS).
BOQ (SAS).
Hence  PAB =
PAB =  QBA (matching angles of congruent triangles)
QBA (matching angles of congruent triangles)
so AP || QB (alternate angles are equal).
b Similarly  QAB =
QAB =  PBA (matching angles of congruent triangles)
PBA (matching angles of congruent triangles)
so AQ || PB (alternate angles are equal).
Hence APBQ is a parallelogram.
Proving the validity of the construction of the perpendicular bisector of an interval
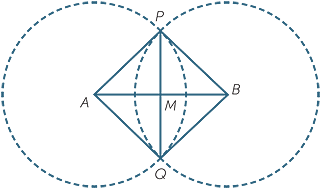
The following exercise uses the SSS and SAS congruence tests to prove the validity of the standard ruler-and-compasses construction of the perpendicular bisector of a given interval.
EXERCISE 4
The circles in the diagram below have centres A and B and the same radius.
a Prove that  APQ
APQ 
 BPQ.
BPQ.
b Hence prove that  APM
APM 
 BPM.
BPM.
c Hence prove that PQ is the perpendicular bisector of AB.
The circumcentre of a triangle
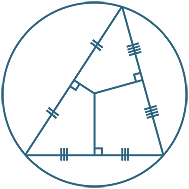 The following exercise proves that the three perpendicular
The following exercise proves that the three perpendicular
bisectors of the sides of a triangle are concurrent.
It also shows that this point is equidistant from all
three vertices, so it is the centre of the circle passing
through all three vertices of the triangle.
The circle is called the cirumcircle and its centre is called its circumcentre.
EXERCISE 5
In the diagram to the right, the points P, Q and R are the midpoints of the sides BC, CA and AB of a triangle ABC. The perpendicular bisectors of the two sides BC and CA of  ABC have been constructed, meeting at O , and RO has been joined.
ABC have been constructed, meeting at O , and RO has been joined.
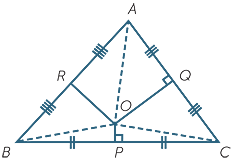 a Prove that
a Prove that  BOP
BOP 
 COP and
COP and  COQ
COQ 
 AOQ.
AOQ.
b Hence show that a circle with centre O passes through the vertices of the triangle.
c Show also that RO is the perpendicular bisector of AB.
Part b proves that O is the circumcentre of the triangle.
Part c proves that the perpendicular bisectors are concurrent.
Demonstrating that the angle in the SAS test must be the included angle
The SAS congruence test requires that the angle be included. The following exercises demonstrate that the test would fail if we allowed non-included angles.
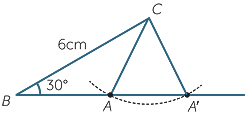
EXAMPLE
Use ruler and compasses to construct two non-congruent triangles ABC with
BC = 6 cm AC = 4 cm  B = 30° (This is a non-included angle)
B = 30° (This is a non-included angle)
Solution
EXERCISE 6
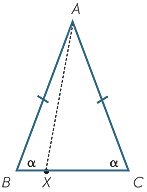 The triangle ABC to the right is isosceles, with
The triangle ABC to the right is isosceles, with
AB = AC and  B =
B =  C.
C.
The point X is any point on the side BC.
Assuming (wrongly) that the SAS test can be applied
when the angles are non-included, prove that
 AXB
AXB 
 AXC, which is clearly false.
AXC, which is clearly false.
The AAS congruence test
Now let us turn attention to the angles of a triangle. If two angles of a triangle are known, then the third angle is also known, because all three add to 180°. But knowing all three angles of a triangle does not determine the triangle up to congruence. To demonstrate this, suppose that we were asked to construct a triangle ABC in which
 C = 45° and
C = 45° and  B = 35°
B = 35°
It now follows that  A = 100°.
A = 100°.
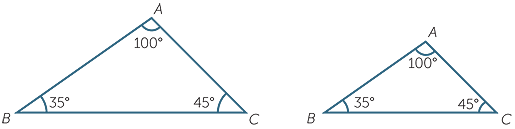
Clearly nothing controls the size of the resulting triangle ABC. Thus knowing that two triangles have the same angle sizes is not enough information to establish congruence.
In the module, Scales Drawings and Similarity we will see that the two triangles are similar.
Constructing a triangle with two angles and a given side
When the angles of a triangle and one side are known, however, there is no longer any freedom for the size to change, so that only one such triangle can be constructed (up to congruence). To demonstrate this, suppose that we are asked to construct a triangle  ABC with these angles and sides length:
ABC with these angles and sides length:
 B = 35°
B = 35°  C = 45° BC = 13cm (It follows that
C = 45° BC = 13cm (It follows that  A = 100°.)
A = 100°.)
The most straightforward way is to draw the interval BC and then construct the angles at the endpoints B and C.
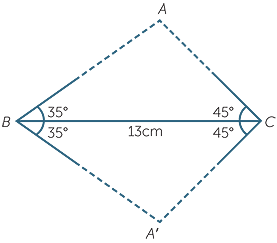
These two triangles ABC and A′BC are congruent, because when the diagram is reflected in the line BC, the interval BA falls on the interval BA′ and the interval CA falls on the interval CA′. A further two congruent triangles can be formed by reflecting in a line through C perpendicular to BC.
This establishes that it is reasonable to take the AAS congruence test as an axiom
of geometry.
The AAS congruence test
- If two angles and one side of a triangle are respectively equal to two angles and the matching side of another triangle, then the two triangles are congruent.
- If we are given the angles sizes of a triangle and the length of a specific side, then only one such triangle can be constructed (up to congruence).
The initials AAS stand for 'Angle', 'Angle', 'Side'.
Notice that this congruence test tells us that the other two sides of a triangle are completely determined by one side and two angles. The sine rule can be used to find the other two side lengths.
EXAMPLE
Show that O is the midpoint of both AQ and BP in the diagram below .
Solution
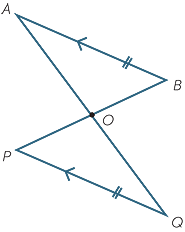 In the triangles AOB and QOP
In the triangles AOB and QOP
|
|
(alternate angles , AB ||PQ) |
|
|
|
(alternate angles , AB || PQ) |
|
|
AB = QP |
(given) |
so  AOB
AOB 
 QOP (AAS)
QOP (AAS)
Hence AO = QO and BO = PO (matching sides of congruent triangles)
That is, O is the midpoint of both AQ and BP.
This example shows that the diagonals of a parallelogram bisect each other.
EXERCISE 7
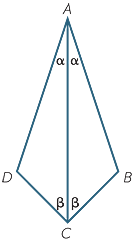 This exercise proves that if one diagonal of a quadrilateral bisects both vertex angles, then the quadrilateral is a kite.
This exercise proves that if one diagonal of a quadrilateral bisects both vertex angles, then the quadrilateral is a kite.
In the diagram to the right, prove that
AB = AD and CB = CD.
(This is the definition of a kite)
The RHS congruence test
We have seen that two sides and a non-included angle are, in general, not enough to determine a triangle up to congruence. When the non-included angle is a right angle, however, we do obtain a valid test. In this situation, one of the two specified sides lies opposite the right angle, and so is the hypotenuse.
The test is therefore given the initials RHS for ‘Right angle’, ‘Hypotenuse, ‘Side’.
RHS congruence test
The hypotenuse and one side of one right-angled triangle are respectively equal to the hypotenuse and one other side of another right-angled triangle then the two triangles are congruent. If we are given the length of the hypotenuse and one other side of a right-angled triangle, then only one such triangle can be constructed (up to congruence).
The initials RHS stand for ‘Right angle’, ‘Hypotenuse’, ‘Side’
This congruence test tells us that the other two angles and the third side of a right-angled triangle are completely determined by the hypotenuse and one other side.
Simple trigonometry will later determine the angles sizes, and the third side can be found by Pythagoras’ theorem. Indeed Pythagoras’ theorem allows us to prove this test is valid very quickly, using the SSS test holds.
Proving the RHS congruence test
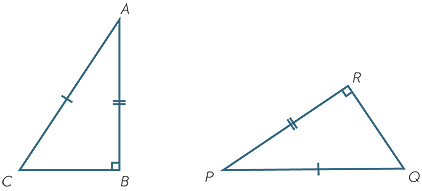
In the triangles above,  B =
B =  R = 90° and AC = PQ and AB = PR.
R = 90° and AC = PQ and AB = PR.
Using Pythagoras’ theorem,
BC2 = AC2 − AB2 = PQ2 − PR2 = QR2
so BC = QR. Hence the two triangles have three pairs of equal sides, and so are congruent by the SSS congruence test.
Constructing a right-angled triangle given the hypotenuse and one side
Suppose that we are asked to construct a right-angled triangle ABC with these specifications:
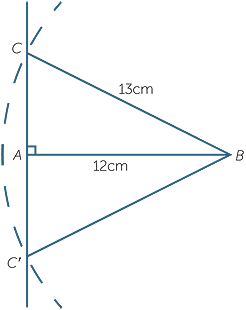
 A = 90° BC = 13cm AB =12cm
A = 90° BC = 13cm AB =12cm
1 Draw an interval AB of length 12 cm.
2 Draw a line through A perpendicular to AB.
3 Draw a circle with centre B and radius 13cm,
cutting the perpendicular line at C and C′ .
4 Join up the triangles  ABC and
ABC and  ABC′.
ABC′.
These two triangles ABC and A′BC are
congruent by the RHS test.
Reflection in the line AB takes the line CAC′ and
the circle onto themselves.
EXERCISE 8
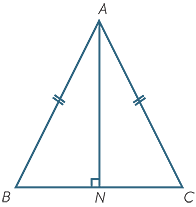 This exercise shows that the altitude to the base of an isosceles triangle bisects the apex angle.
This exercise shows that the altitude to the base of an isosceles triangle bisects the apex angle.
a Prove that  ABN
ABN 
 ACN.
ACN.
b Hence show that AN bisects  A.
A.
The incentre of a triangle
The following exercise proves that the three angle bisectors of a triangle are concurrent. It also shows that this point has the same perpendicular distance from each side of the triangle. By some later results concerning circles and their tangents, it is the centre of a circle tangent to all three sides of the triangle.
The circle is called the incircle and the point is called the incentre.
EXERCISE 9
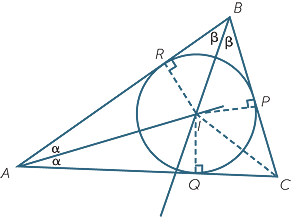 In the diagram to the right, the angle bisectors of
In the diagram to the right, the angle bisectors of  A and
A and  B meet at I , and the interval IC is joined.
B meet at I , and the interval IC is joined.
Perpendiculars are drawn from I to the three sides.
a Prove that  IAQ
IAQ 
 IAR and
IAR and  IBR
IBR 
 IBP .
IBP .
b Hence show that IP = IQ = IR.
c Hence show that the interval IC bisects  C .
C .
Part b shows that I is the centre of the circle which touches all three sides.
Part c shows that the three angle bisectors are concurrent.
A further test for congruence − Extension
We have seen that there is no ‘ASS test’, meaning ‘two pairs of equal sides and a pair of matching non-included angles’, but that when the non-included angle is a right angle, there is a valid test. The following exercise shows that there is also a valid test when the non-included angle is an obtuse angle − this test, however, is not part of standard geometry courses in school.
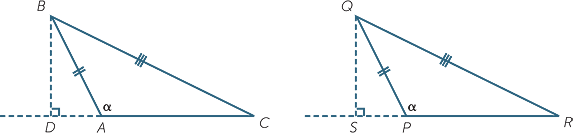
EXERCISE 10
The diagram above shows triangles ABC and PQR with
 A =
A =  P = α > 90° and AB = PQ and BC = QR
P = α > 90° and AB = PQ and BC = QR
Construct the perpendiculars BD from B to CA produced, and QS from Q to RP produced.
a Prove that  ABD
ABD 
 PQS.
PQS.
b Hence prove that  BDC
BDC 
 QSR.
QSR.
c Hence prove that  ABC
ABC 
 PQR.
PQR.
d Why is this proof not valid when  A and
A and  P are acute? (Draw diagrams)
P are acute? (Draw diagrams)
Isosceles and equilateral triangles
Congruence is needed in the theory of isosceles and equilateral triangles.
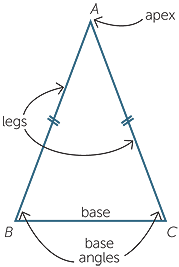
ISOSCELES AND EQUILATERAL TRIANGLES
- An isosceles triangle is a triangle with two (or more) sides equal.
- The equal sides are called the legs and the third side is called the base.
- The legs meet at the apex and the other two angles are the base angles.
- An equilateral triangle is a triangle with all three sides equal.
The word 'isosceles' comes from Greek and means 'equal legs'.
The word 'equilateral' comes from Latin and means 'equal sides'.
 |
 |
||
| An isosceles triangle | An equilateral triangle |
The base angles of an isosceles triangle are equal
Congruence allows us to give a formal proof of this result. We have set out the full proof below in a manner appropriate for Years 7−8 students learning how to proceed from a theorem stated in general terms to its proof using a particular diagram.
Theorem:
The base angles of an isosceles triangles are equal.
Proof:
Let  ABC be isosceles, with AB = AC.
ABC be isosceles, with AB = AC.
We prove that  B =
B =  C.
C.
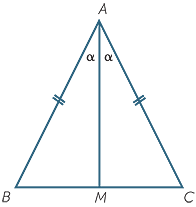 Let AM be the bisector of
Let AM be the bisector of  A
A
In the triangles ABM and ACM:
| AB = AC | (given) | ||
| AM = AM | (common) | ||
 BAM = BAM =  CAM CAM |
(construction) | ||
so  ABM = ABM =  ACM ACM |
(SAS). | ||
Hence |
(matching angles of congruent triangles). |
EXERCISE 11
Explain how else could the interval AM have been constructed in the previous proof?
How would this have changed the proof?
A test for a triangle to be isosceles
The converse of the previous result is also true, and gives a test for a triangle
to be isosceles.
EXERCISE 12
M is a point on BC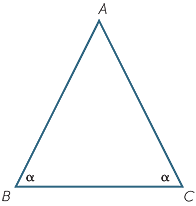
a Let AM be the angle bisector of  A.
A.
Prove that AB = AC.
b Assuming only that AM is an altitude, can you prove that AB = AC?
c Assuming only that M is the midpoint of BC, can you prove that AB = AC?
EXERCISE 13
The Greek mathematician Pappus (Alexandria, early 4th century AD) took an interesting approach to these results, by noting that the triangle is congruent to itself in a different orientation.
a If  ABC is isosceles with AB = AC, explain why
ABC is isosceles with AB = AC, explain why  ABC
ABC 
 ACB, and hence prove that
ACB, and hence prove that  B =
B =  C .
C .
b Conversely, if  ABC has
ABC has  B =
B =  C, explain why
C, explain why  ABC
ABC 
 ACB, and hence prove that AB = AC.
ACB, and hence prove that AB = AC.
Equilateral triangles
An equilateral triangle is a triangle with three equal sides.
An equilateral triangle is an isosceles triangle in all its six orientations, so by the theorem on the base angles of an isosceles triangle, all its angles are equal. Since the sum of its angles is 180°, each angle is 60°.
Conversely, if all the angles of a triangle are equal, then by the converse theorem, all its sides are equal, and it is therefore equilateral.
Isosceles triangles
- The base angles of an isosceles triangle are equal.
- Conversely, if two angles of a triangle are equal, then the sides opposite those angles are equal. (That is, the triangle is isosceles.)
Equilateral triangles
- The interior angles of an equilateral triangle are all 60°.
- Conversely if all the angles of a triangle are equal, then the triangle is equilateral.
EXERCISE 14
There are many correct answers to both of the following questions.
a It is clearly false to claim that any two equilateral triangles are congruent. Complete the sentence, ‘Two equilateral triangles are congruent if …’
b Complete the sentence, ‘Two isosceles triangles are congruent if …’
An alternative construction of a right angle at the endpoint of an interval.
To construct a right angle at the endpoint A of an interval AB:
- Draw a circle with centre A and any radius, cutting AB at X.
- With centre X and the same radius, draw an arc cutting
the line at Y. - Join XY and produce the line more than twice as far.
- With centre Y and the same radius, draw an arc cutting
the line at Z.
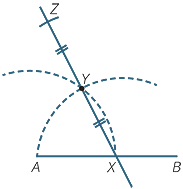
Then AZ ⊥ AB.
EXERCISE 15
Prove that this construction works.
The congruence tests allow the theory of special triangles and quadrilaterals to be developed. In particular, some of the proofs of the constructions can be understood as consequences of the properties of kites. The four similarity tests are developed as generalisations of the four congruence tests. Similarity and congruence are widely used in circle geometry.
As we have discussed, each congruence tests can also be regarded as a set of specifications for constructing a triangle up to congruence. Trigonometry is needed to calculate the missing lengths and angles in such a specification.
SAS test: The cosine rule allows the side to be calculated. If the sides b and c and the size of A and are known in  ABC , then the side a can be found using the formula
ABC , then the side a can be found using the formula
![]() a2 = b2 + c2 − 2bc cos A.
a2 = b2 + c2 − 2bc cos A.
SSS test: The cosine rule allows each angle to be calculated. If the three sides of
 ABC are known, then
ABC are known, then  A can be found by solving the formula above for cos A.
A can be found by solving the formula above for cos A.
AAS test: The sine rule allows the other two sides to be calculated. If the three angles and the side a of  ABC are known, then the sides b and c can be found using the formula
ABC are known, then the sides b and c can be found using the formula
![]()
 =
= 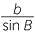 =
= 
RHS test: Simple trigonometry and Pythagoras’ theorem are sufficient for calculations in a right-angled triangle.
The sine rule in reverse may be ambiguous, because, for example, θ = 30° and θ = 150° are both solutions of sin θ =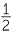 . This corresponds to the fact that there is no ‘ASS test’ − two sides and a non-included angle − unless the given angle is a right angle (or obtuse as shown in an extension exercise.)
. This corresponds to the fact that there is no ‘ASS test’ − two sides and a non-included angle − unless the given angle is a right angle (or obtuse as shown in an extension exercise.)
Congruence can also be applied to figures with curves, but in such figures congruent triangles may be insufficient and some direct appeal to transformations may be required. The following is a very simple example of such a situation.
EXAMPLE
Prove that two arcs of a circle are equal if and only if they subtend the same angle
at the centre.
Solution
 In the diagram to the right, suppose first that the arcs
In the diagram to the right, suppose first that the arcs
AB and PQ have equal length. Then rotating the circle
about its centre until OA lies on OP will transform
B to Q, so  AOB =
AOB =  POQ.
POQ.
Conversely, suppose that  AOB =
AOB =  POQ. Then again, rotating the circle about its centre until OA lies on OP will transform B to Q, so the arcs AB and PQ have equal length.
POQ. Then again, rotating the circle about its centre until OA lies on OP will transform B to Q, so the arcs AB and PQ have equal length.
Euclid wrote his mathematics book, called the Elements, in Alexandria around 300 BC. It starts and finishes with geometry, but along the way deals with such things as quadratic equations, ratio and proportions, and prime numbers, all treated with a distinctly geometric flavour. The book is distinguished by its impressive rigour, and by its systematic arrangement of its material into a logical sequence of definitions and theorems, based on carefully formulated axioms that are taken as its initial assumptions. This approach became the paradigm for the organisation and the logical rigour of modern mathematics, and also inspired similar attempts to organise the structure of other disciplines, particularly parts of philosophy and theology. Euclid’s book also became the most famous textbook in mathematics, and was still being used as the standard text for school geometry well into the 20th century.
Congruence is an essential part of the early logical foundation of Euclid’s geometry, and remains so in our present school courses. Euclid only states three congruence tests − our SSS, SAS and AAS tests − to which we now find it convenient to add the RHS test. The notes in this module proved the RHS test in terms of the other tests, but we took Euclid’s three tests as axioms of geometry. We merely demonstrated the reasonableness of these axioms by showing how to construct triangles specified by side lengths and angle sizes corresponding to the tests.
The concept of ‘moving one triangle to fit exactly on top of the other’ is not regarded nowadays by mathematicians as a satisfactory starting point for congruence, but it is perfectly satisfactory for school geometry. Euclid’s development of the congruence tests uses this idea very cleverly, and his actual text could well be used as extension in Years 9−10 − it was, after all, the standard school geometry textbook not so long ago. A very clear web presentation of Euclid’s Elements can be found at https://aleph0.clarku.edu/~djoyce/java/elements/toc.html where a complete translation of the text is accompanied by extremely clear diagrams, cross- referencing, and an excellent explanatory commentary. The congruence tests are proven in Propositions 4, 8 and 26 of Book 1.
Euclid’s work is interesting for second reason − it uses geometry as a means of dealing with arithmetic and algebra. Contrast this with Descartes’ idea of the coordinate plane, introduced in the early 17th century, which interpreted points as pairs of numbers and lines and curves as equations, and showed how Euclid’s geometrical results could be obtained using algebra and arithmetic. Geometry and arithmetic can both be used as bases for mathematics.
Vector geometry was developed in the 19th century from Cartesian and Euclidean geometry, and became the usual way to study phenomena like electro-magnetism that require a combination of calculus and geometry. Modern mathematics and modern physics routinely move between algebraic-arithmetic ideas and geometric ideas, using at any point whichever approach gives a significant intuition about the situation or provides the clearest proof. Modern mathematics and physics are as inconceivable without geometry as they are without algebra.
EXERCISE 1
Each side length must be lesser than the sum of the other two side lengths
EXERCISE 2
In the triangles OMX and OMY:
|
1. |
OX |
= OY |
(radii of the same circle) |
|
|
2. |
XM |
= YM |
(radii of circles of equal radii) |
|
|
3. |
OM |
= OM |
(common) |
|
|
so |
|
|
(SSS) |
|
|
Hence |
|
= |
(matching angles of congruent triangles). |
|
EXERCISE 3
By the SSS congruence test,  OAB and
OAB and  PFG are congruent isosceles triangles.
PFG are congruent isosceles triangles.
Hence  AOB =
AOB =  FPG (matching angles of congruent triangles).
FPG (matching angles of congruent triangles).
EXERCISE 4
a Use the SSS congruence test.
b Hence  APM =
APM =  BPM, so
BPM, so  APM
APM 
 BPM by the SAS congruence test.
BPM by the SAS congruence test.
c These now follow from part b.
EXERCISE 5
a Use the SAS congruence test.
b Using matching sides of congruent triangles, AO = BO = CO.
c By the SSS congruence test,  AOR
AOR 
 BOR.
BOR.
Hence  ARO =
ARO =  BRO (matching angles of congruent triangles):
BRO (matching angles of congruent triangles):
But  ARO +
ARO +  BRO = 180° (straight angle).
BRO = 180° (straight angle).
Hence  ARN =
ARN =  BRN = 90°.
BRN = 90°.
EXERCISE 6
In the triangles AXB and AXC:
1. AX = AX (common)
2. AB = AC (given)
3.  B =
B =  C (given)
C (given)
so  AXB
AXB 
 AXC (SAS)
AXC (SAS)
This argument is invalid because the angles are not included.
EXERCISE 7
Use the AAS congruence test.
EXERCISE 8
a Use the RHS congruence test.
b Use matching angles of congruent triangles.
EXERCISE 9
a Use the AAS congruence test.
b Use matching sides of congruent triangles.
c From part b,  ICP
ICP 
 ICQ by the RHS congruence test, from which the bisection follows.
ICQ by the RHS congruence test, from which the bisection follows.
EXERCISE 10
a Use the SAS congruence test.
b Hence BD = QS, so use the RHS congruence test.
c Hence  C =
C =  R, so use the AAS congruence test.
R, so use the AAS congruence test.
d When  A is acute, the constructed point D lies inside the interval AC if
A is acute, the constructed point D lies inside the interval AC if  C is acute, and outside if
C is acute, and outside if  C is obtuse, and similarly for the constructed point S. Thus there may be two possible non-congruent triangles.
C is obtuse, and similarly for the constructed point S. Thus there may be two possible non-congruent triangles.
EXERCISE 11
a We could have let M be the midpoint of BC and joined AM. This would require the SSS congruence test.
b We could have let AM be the altitude to BC from A. This would require the RHS congruence test.
EXERCISE 12
a Construct the angle bisector of  A, meeting BC at M, and use the AAS test.
A, meeting BC at M, and use the AAS test.
b Construct the altitude from A, meeting BC at M, and use the AAS test.
c The interval joining A to the midpoint of BC will not help, because it involves the non-
included angle situation.
EXERCISE 13
a Use the SSS or the SAS congruence test, then use matching sides.
b Use the AAS congruence test, then use matching angles.
EXERCISE 14
a The most obvious answers are ‘…if they have the same side lengths’, or ‘…if they have the same perpendicular height’, or ‘…if they have the same area’.
b Some obvious answers are ‘…if they have the same side lengths’, or ‘…if they have the same base and perpendicular height’, or ‘…if they have the same base and base angles’, or ‘…if they have the same base angles and leg length, or ‘…if they have the same area and base’.
EXERCISE 15
 AXY is equilateral', because its sides are radii of circles of equal radii,
AXY is equilateral', because its sides are radii of circles of equal radii,
so  AYZ = 120° (exterior angle of
AYZ = 120° (exterior angle of  AXY),
AXY),
so  ZAY =
ZAY =  AZY = 30° (angle sum of isosceles
AZY = 30° (angle sum of isosceles  AYZ).
AYZ).
Hence  ZAB = 90° (adjacent angles).
ZAB = 90° (adjacent angles).
[Alternatively,  ZAX is an angle in the semicircle with diameter XYZ, but this requires some circle geometry.]
ZAX is an angle in the semicircle with diameter XYZ, but this requires some circle geometry.]
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


