The Improving Mathematics Education in Schools (TIMES) Project
Scale drawings and similarity
Measurement and Geometry : Module 22![]() Years : 8-10
Years : 8-10
June 2011
- Translations, reflections and rotations.
- Elementary Euclidean geometry, including constructions and transversals
to parallel lines. - Ratio, fractions and the unitary method.
- Sections 3−6 on similarity assume that congruence has already been studied.
Scale drawings are used when we increase or reduce the size of an object so that it fits nicely on a page or computer screen. For example, we would want to reduce the size when drawing:
- the plan of the facade of a building
- a map of a suburb or a country
- a photograph of a distant galaxy,
and we would want to increase the size when drawing:
- a diagram of a printed circuit
- a magnified photograph of an insect
- a drawing of a human cell.
The proportional increase or decrease in lengths is called the scale of the drawing. It is usually expressed in terms of a ratio, so the topic of scale drawings is closely related to ratios and fractions.
The transformation that produces a scale drawing is an enlargement. An enlargement transformation preserves the shape of the figure, but increases or decreases all distances by a constant ratio.
This is different from the three transformations that we have already introduced − translations, rotations and reflections all produce an image that is the same size and shape as the original figure.
The module, Congruence studied congruent figures, which are figures that can be mapped one to the other by a sequence of translations, rotations and reflections. Figures that can be mapped one to the other by these transformations and enlargements are called similar. Thus two figures are similar if an enlargement of one is congruent to the other.
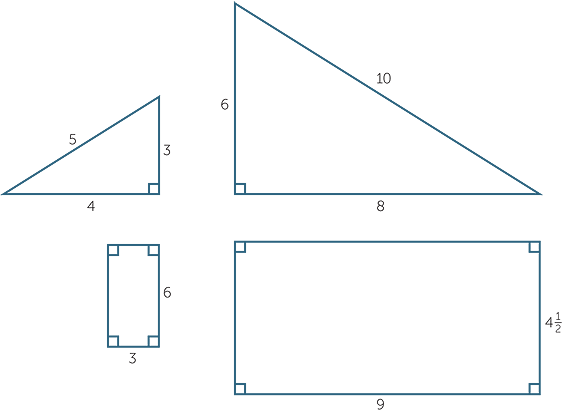
Any two figures that have the same shape are similar. Matching angles in similar figures are equal, but matching lengths in two similar figures are all in the same ratio. This constant ratio is the same ratio that appears in scale drawings and enlargements.
The theory of similarity develops in the same way as congruence. First, most situations involving similarity can be reduced to similar triangles, and we shall establish four similarity tests for triangles, corresponding to the four congruence tests for triangles. Secondly, just as congruence was used to prove many basic theorems about triangles and special quadrilaterals, so similarity will allow us to establish further important theorems in geometry.
The treatment of similarity and enlargements in this module has been guided by well-established classroom practice. Scale drawings and enlargements are usually discussed a year or so earlier than similarity, and these topics therefore receive a self-contained treatment in Sections 1−2.
Section 3 can then introduce similarity in terms of enlargement transformations. In Section 4−6, the discussion of similar triangles begins with the AAA similarity test, which is usually considered the most straightforward test to use.
A scale drawing has exactly the same shape as the original object, but usually has a different size.
This means that:
- Matching angles in the original and the drawing are equal, and
- All the lengths of the original object are reduced or magnified in the drawing in exactly the same ratio. This ratio is called the scale of the drawing.
![]() Scale = length on the drawing : length on the actual object
Scale = length on the drawing : length on the actual object
The scale of a drawing is thus given as the ratio of two numbers. For example, in the photograph below, showing the side of a train engine,
![]() Scale = 1 : 200.
Scale = 1 : 200.

This means that a length of 1 cm on the photograph above corresponds to a length of 200 cm , or 2 metres, on the actual engine. The scale can also be written as the ratio of two lengths,
![]() Scale = 1 cm : 2 m
Scale = 1 cm : 2 m
This second notation, using the ratio of two lengths with different units, is often more convenient for maps, where, for example, a scale of 1 cm : 100 km is easier to interpret than 1 : 10 000 000.
Example
- a
- Measure the overall length of the engine in the photograph above, including the couplings. Then use the scale to find the approximate length of the actual engine.
- b
- Find the approximate width and height of the doors, and the area of each door.
Solution
a![]() Engine length in photograph = 11 cm
Engine length in photograph = 11 cm
 |
Actual engine length | = 2200 cm | ||
| = 22 metres |
b![]() Width of door in photograph = 0.35 cm
Width of door in photograph = 0.35 cm
 |
Actual width of door | = 70 cm | ||
| = 0.7 metres |
Height of door in photograph = 1.1 cm
 |
Actual height of door | = 220 cm |
||
| = 2.2 metres | ||||
| Area of door | = 0.7 × 2.2 | ||||
| = 1.54 m2 | |||||
Example
| a | Convert each scale to a ratio of two numbers. | ||||||
| i | 6 m : 1 cm | ii | 6 cm : 10 km | ||||
| b | Convert each scale to a ratio of lengths in the units indicated. | ||||||
| i | 400 : 1 = 1 cm : … mm | ii | 1 : 150 000 = 1 cm : …km | ||||
Solution
| a | i 6 m : 1 cm | = 600 cm : 1 cm | ii | 6 cm : 10 km | = 6 cm : 1 000 000 cm | |||
| = 600 : 1. | = 3 : 500 000. |
When the scale is written as a ratio of two numbers, the ratio is normally cancelled down to simplest form.
| b | i 400 : 1 | = 400 cm : 1 cm | ii | 1 : 150 000 | = 1 cm : 150 000 cm | |||
| = 4 cm : 0.1 mm | = 1 cm : 1500 m | |||||||
| = 1 cm : 0.025 mm | = 1 cm : 1.5 km |
SCALE DRAWINGS:
- A scale drawing of an object has the same shape as the object, but a different size.
- The scale of the drawing is the ratio length on the drawing : length on the actual object.
- A scale can be written as the ratio of two lengths, or as the ratio of two numbers.
For example: scale = 1 cm : 5 m or scale = 1 : 500 - Matching angles are equal, and the ratio of matching lengths equals the scale.
EXERCISE 1
The photograph below shows the facade of the neo-Gothic St Petrus and Paulus Church in Ostend, Belgium. Assume that the person dressed in a black suit in the bottom right-hand corner of the photograph is 2 metres tall.
a![]() What is the approximate scale of the photograph?
What is the approximate scale of the photograph?
b![]() What is the approximate height of the top of each spire from the ground?
What is the approximate height of the top of each spire from the ground?

Scales involving very large and very small distances − Scientific notation
Science routinely uses scale drawings and photographs of astronomical and microscopic objects. When the scale of such drawings is expressed in terms of pure numbers, the numbers are so large, or so small, that scientific notation becomes appropriate.
EXAMPLE
- a
- A distant galaxy with diameter 100 000 light years appears on a photograph as an image with diameter 3 cm. Given that a light year is very roughly 1013 km, express this scale as the ratio of two numbers.
- b
- A molecule with diameter 10 Angstrom units across appears on an electron microscope photograph as an image with diameter 5 cm. Given that 1 Angstromunit
is 10-10 metres, express this scale as the ratio of two numbers.
Solution
- a
- 3 cm : 105 light years = 3 cm : 105 × 1013 × 105 cm = 3 : 1023.
- b
- 5 cm : 10 Angstrom units = 5 cm : 10 × 10-10 × 100 cm = 5 : 10-7 = 5 × 107 : 1.
The best form for the answer to this question is 1 : 2 × 10-8 or 5 × 107 : 1.
We have already dealt with three transformations of the plane − translations, rotations and reflections. These three transformations are examples of congruence transformations, because the image of a figure under one of these transformations is congruent to the original. Indeed, we defined two figures to be congruent if one could be mapped to the other by a sequence of these transformations.
This section introduces a fourth type of transformation of the plane called an enlargement, in which all lengths are increased or decreased in the same ratio.
To specify an enlargement, we need to specify two things:
- The centre O of the enlargement. The centre of enlargement stays fixed in the one place, while the enlargement expands or shrinks everything else around it.
- An enlargement factor k (or enlargement ratio 1 : k). The distances of all points from the enlargement centre increase or decrease by this factor.
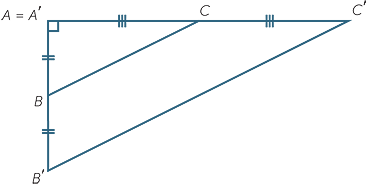
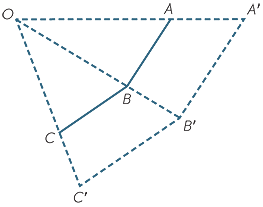
In this module, we will only deal with positive enlargement factors. For example, the diagram below shows a point O and a triangle ABC.
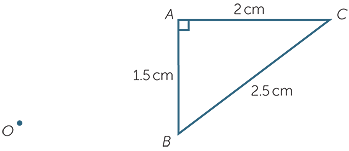
The next figure below shows how to construct the image  A′B′C′ of
A′B′C′ of  ABC under the enlargement with centre O and enlargement factor 2. Because the construction only involves doubling, it can be done with straight edge and compasses.
ABC under the enlargement with centre O and enlargement factor 2. Because the construction only involves doubling, it can be done with straight edge and compasses.
- Join OA, then extend OA to OA′ so that OA′ = 2 × OA.
- Join OB, then extend OB to OB′ so that OB′ = 2 × OB.
- Join OC, then extend OC to OC′ so that OC′ = 2 × OC.
- Join up the triangle A′B′C′, which is called the image of
 ABC.
ABC.
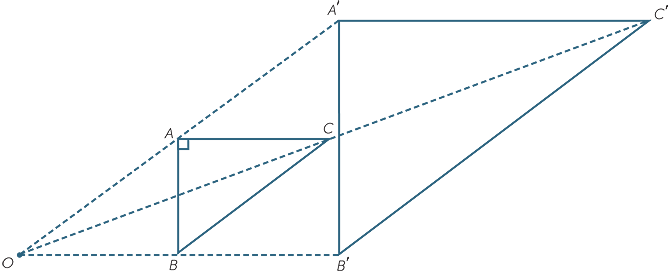
We can use this diagram to verify three important properties of enlargements.
First, it is easy to verify with compasses that each side of the image triangle A′B′C′ is twice the length of the matching sides of the original triangle ABC. That is,
![]()
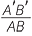 = 2,
= 2, 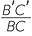 = 2 and
= 2 and 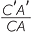 = 2.
= 2.
Secondly, we can verify that each angle of  A′B′C′ is equal to the matching angle of
A′B′C′ is equal to the matching angle of  ABC.
ABC.
![]()
 B′A′C′ =
B′A′C′ =  BAC,
BAC,  A′C′B′ =
A′C′B′ =  ACB and
ACB and  C′B′A′ =
C′B′A′ =  CBA.
CBA.
Thirdly, since the corresponding angles are equal, each side of the image triangle is parallel to the matching side of the original triangle:
![]() A′B′ || AB, B′C′ || BC and C′A′ || CA.
A′B′ || AB, B′C′ || BC and C′A′ || CA.
It follows from the first and second points above that the image  A′B′C′ is a scale drawing of the original figure
A′B′C′ is a scale drawing of the original figure  ABC, with ratio 1 : 2. If we had used a different centre of enlargement, but the same enlargement factor 2, then the image
ABC, with ratio 1 : 2. If we had used a different centre of enlargement, but the same enlargement factor 2, then the image  A′B′C′ would end up in a different place, but it would still be a scale drawing with ratio 1 : 2. For example, the diagram below uses the vertex A as the centre of enlargement.
A′B′C′ would end up in a different place, but it would still be a scale drawing with ratio 1 : 2. For example, the diagram below uses the vertex A as the centre of enlargement.
Enlargements are reversible. In our examples above,  ABC is the image of
ABC is the image of  A′B′C′ under an enlargement with the same centre O, but enlargement factor
A′B′C′ under an enlargement with the same centre O, but enlargement factor  , and
, and  ABC is a scale drawing of
ABC is a scale drawing of  A′B′C′ with ratio 2 : 1. To perform the construction given the point O and the triangle A′B′C′, we would obtain the points A, B and C by bisecting each interval OA′, OB′ and OC′.
A′B′C′ with ratio 2 : 1. To perform the construction given the point O and the triangle A′B′C′, we would obtain the points A, B and C by bisecting each interval OA′, OB′ and OC′.
An enlargement can have any positive real number as its enlargement factor. The definition and the properties of enlargements are summarised in the box below.
ENLARGEMENT TRANSFORMATIONS:
- An enlargement is specified by a centre of enlargement and an enlargement factor k > 0.
- The enlargement moves each point P to a point P′ on the ray OP.
- The distance OP′ is k times the distance OP. That is, OP′ = k × OP.

- If k > 1, then the image is larger than the original.
- If k < 1, then the image is smaller than the original.
- If k = 1, then no point moves, and the image is the same as the original.
PROPERTIES OF AN ENLARGEMENT:
- The image of an interval is k times the length of the original interval.
- The image of an angle has the same size as the original angle.
- The image of an interval is parallel to the original interval.
The following exercise is intended to present two further examples of enlargements, and to confirm that in these two cases, each distance is increased by the enlargement factor.
EXERCISE 2
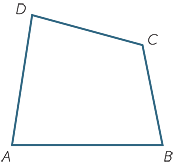
- a
- i
- Using A as the centre of enlargement and enlargement factor 3, construct the image AB′C′D′ of the quadrilateral ABCD.
- ii
- Confirm that:
- B′C′ = 3 × BC and D′C′ = 3 × DC, and
B′C′ = 3 × BC and D′C′ = 3 × DC, and
- the images
the images  B′,
B′,  C′ and
C′ and  D′ are each equal to the original angle.
D′ are each equal to the original angle.
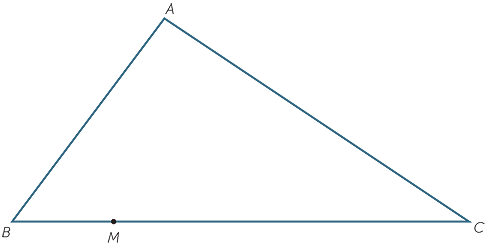
- b
- i

- Using M as the centre of enlargement and enlargement factor
 , construct the image
, construct the image  A′B′C′ of the isosceles triangle ABC.
A′B′C′ of the isosceles triangle ABC. - ii
- Confirm that:
- each interval of the image has half the length of the original interval, and
each interval of the image has half the length of the original interval, and
- each angle of the image is equal to the original angle.
each angle of the image is equal to the original angle.
Two plane figures are called similar if an enlargement of one figure is congruent to the other.
That is, if one can be mapped to the other by a sequence of translations, rotations, reflections and enlargements. Similar figures thus have the same shape, but not necessarily the same size.
Thus a scale drawing of a two-dimensional object, and an enlargement of a plane figure, bith produce figures similar to the original.
It follows from the properties of enlargements discussed in the previous section that when two figures are similar:
- matching angles are equal, and
- matching distances are in a constant ratio.
Conversely, if two figures can be matched up so that these two conditions apply, we can enlarge the first figure by the constant ratio. The enlarged figure is thus congruent to the second figure, so the first and second figures are similar.
The constant ratio is called the similarity ratio or similarity factor. If two figures are similar with similarity ratio 1 : 1, then the two figures are congruent, otherwise they will have different sizes.
![]()
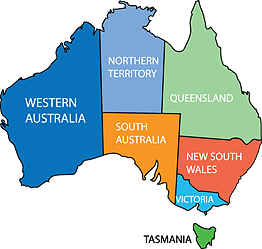
The two maps above are similar to each other. Each distance on the second map is twice the matching distance on the first map, so we say that the similarity ratio is 1 : 2, or that the similarity factor is 2.
In the language of the first section, each map is a scale drawing of Australia (ignoring the curvature of the Earth), and each map is a scale drawing of the other map. We can continue to solve problems in similarity using the unitary method approach adopted with scale drawings, but it is more usual to use algebra and fractions, as in the following example.
As with congruence, vertices must be kept in matching order.
Example
The two parallelograms below are known to be similar.
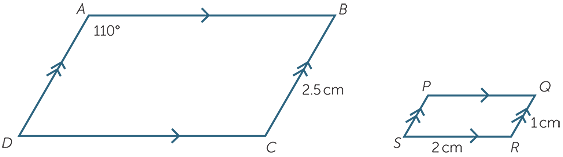
a![]() What is the size of
What is the size of  P?
P?
b![]() Find the base DC of the large parallelogram.
Find the base DC of the large parallelogram.
c![]() Find the similarity ratio of:
Find the similarity ratio of:
![]() i
i![]() PQRS to ABCD,
PQRS to ABCD, ![]() ii
ii![]() ABCD to PQRS.
ABCD to PQRS.
Solution
| a |  P = 110° P = 110° |
(matching angles of similar figures) | |||||
| b | 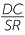 = = 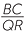 |
(matching sides of similar figures) | or | 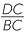 |
= 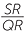 |
||
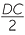 = =  |
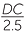 |
= 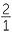 |
|||||
| DC = 5 cm | DC | = 5 cm | |||||
| c | i |
ii | 2.5 : 1 or 5 : 2 | ||||
Both methods of writing the algebra of part b are equally good.
- In the first method, one pair of matching intervals is on the left of the equation, the other pair is on the right.
- In the second method, two intervals of one figure are on the left of the equation, and two matching intervals of the other figure are on the right.
One should use whichever method seems more natural at the time − this will often depend on the particular problem. The subsequent algebra will be easier, however, if one always starts by placing the unknown length on the top of the left-hand side.
It is worthwhile writing down the algebra that proves that the two identities are equivalent:
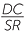 = = 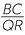 |
||
| DC × QR = BC × SR | (multiplying both sides by SR and by QR) | |
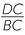 = = 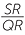 |
(dividing both sides by BC and by QR). |
The middle identity says that two products of lengths are equal. In later work, particularly with circle geometry, this middle identity will be a common way of expressing the consequences of similarity.
Some may prefer to find the length DC by continuing with the arithmetic approach used in scale drawings. Such an approach is not recommended, because it is unsuitable when similarity is applied to more general situations where the similarity ratio is not readily apparent.
Comparing the sides QR and BC, the similarity ratio is 1 : 2.5.
| Hence | DC | = 2.5 × SR |
| = 2.5 × 2 | ||
| = 5 cm |
Exercise 3
Is each statement true or false? If it is false, can you qualify the statement to make it true?
a ![]() Any two squares are similar.
Any two squares are similar.
b ![]() Any two rectangles are similar.
Any two rectangles are similar.
c ![]() Any two rhombuses are similar.
Any two rhombuses are similar.
d![]() Any two circles are similar.
Any two circles are similar.
e![]() Any two sectors of circles are similar.
Any two sectors of circles are similar.
f ![]() Any two equilateral triangles are similar.
Any two equilateral triangles are similar.
g ![]() Any two isosceles triangles are similar.
Any two isosceles triangles are similar.
Four similarity tests for triangles
Two figures are congruent when they are similar with similarity factor 1. Similarity is thus a generalisation of congruence, and we would expect the theory of similarity to proceed along similar lines to the theory of congruence that we have already developed. As with congruence, discussions involving the similarity of straight-sided figures can be reduced to discussions of similar triangles.
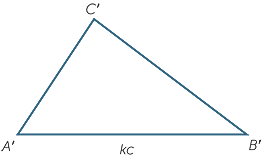
Triangles have three vertex angles and three side lengths. If the vertices of two triangles can be matched up so that matching angles are equal and matching sides are in a constant ratio, then the two triangles are similar.
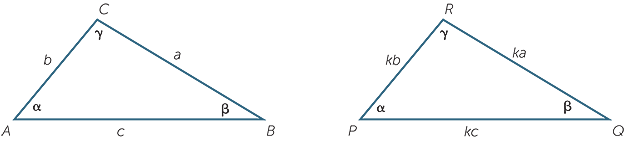
This can be demonstrated with the two triangles above, where matching angles are equal and matching sides are in the ratio 1 : k. We can enlarge  ABC on the left by an enlargement with centre A and enlargement factor k to produce the triangle AB′C′,
ABC on the left by an enlargement with centre A and enlargement factor k to produce the triangle AB′C′,
which is congruent to  PQR on the right. This shows that
PQR on the right. This shows that  ABC is similar to
ABC is similar to  PQR.
PQR.
As with congruent triangles, however, we do not need to check all six measurements to be sure that the two triangles are similar. There are four standard tests for two triangles to be similar, corresponding to the four standard congruence tests.
We can develop each similarity test from the corresponding congruence test. First, the AAS congruence test corresponds to the AAA similarity test, which states:
- The AAA similarity test: If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
If two triangles have two pairs of equal angles, then their third pair is also equal because the angle sum of a triangle is 180°. Thus two such triangles are called equi-angular, and the test is often referred to as the AAA similarity test.
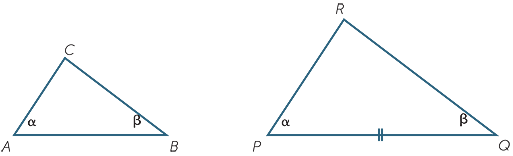
To prove this test, let  ABC and
ABC and  PQR be triangles with
PQR be triangles with
![]()
 A =
A =  P = α and
P = α and  B =
B =  Q = β.
Q = β.
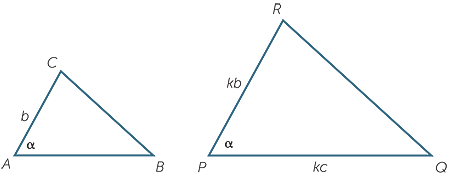
 Enlarge
Enlarge  ABC to
ABC to  A′B′C′ by a suitable
A′B′C′ by a suitable
enlargement factor so that A′B′ = PQ.
Then  A′ = α and
A′ = α and  B′ = β because angles are preserved by enlargements.
B′ = β because angles are preserved by enlargements.
Hence  A′B′C′ is congruent to
A′B′C′ is congruent to  PQR by the AAS congruence test, so
PQR by the AAS congruence test, so  ABC is similar to
ABC is similar to  PQR, because an enlargement of
PQR, because an enlargement of  ABC is congruent to
ABC is congruent to  PQR.
PQR.
This same argument can be applied to develop a similarity test from each of the other three congruence tests. From the SAS congruence test we obtain the SAS similarity test:
- The SAS similarity test: If the ratio of the lengths of two sides of one triangle is equal to the ratio of the lengths of two sides of another triangle, and the included angles are equal, then the two triangles are similar.
![]()
From the SSS congruence test we obtain the SSS similarity test:
- The SSS similarity test: If we can match up the sides of one triangle with the sides of another so that the ratios of matching sides are equal, then the two triangles are similar.
![]()
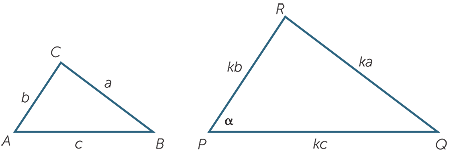
From the RHS congruence test we obtain the RHS similarity test:
- The RHS similarity test: If the ratio of the hypotenuse and one side of a right-angled triangle is equal to the ratio of the hypotenuse and one side of another right-angled triangle, then the two triangles are similar.
![]()
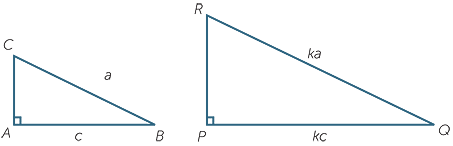
Exercise 4
Develop the SSS similarity test from the SSS congruence test. Use the same argument as was used above to develop the AAA similarity test from the AAS congruence test.
Refer to the triangles ABC and PQR that illustrate the statement of the SSS similarity test above.
Using the AAA similarity test
Similarity problems are set out in much the same way as congruence problems.
In particular, vertices must always be written in matching order in every statement.
The following example shows how to use the AAA similarity test to find lengths. There are two ways of writing the ratio condition on the sides, as discussed in the previous section, and the first example has been solved both ways.
Example
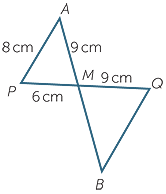 In the diagram to the right:
In the diagram to the right:
a![]() Show that
Show that  AMP is similar to
AMP is similar to  BMQ.
BMQ.
b![]() Hence find:
Hence find: ![]() i
i![]() BQ,
BQ, ![]() ii
ii![]() BM.
BM.
Solution
a![]() In the triangles AMP and BMQ:
In the triangles AMP and BMQ:
 AMP AMP |
=  BMQ BMQ |
(vertically opposite angles) | |
 A A |
=  B B |
(alternate angles, AP || QB) |
![]() so
so  AMP is similar to
AMP is similar to  BMQ (AAA similarity test).
BMQ (AAA similarity test).
b![]() i
i![]() Hence
Hence 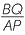 =
= 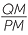
![]() (matching sides of similar triangles)
(matching sides of similar triangles) ![]() or
or![]()
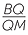 =
= 
 |
=  |
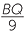 |
= 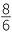 |
||
| BQ | = 8 ×  |
BQ | = 9 ×  |
||
| = 12 cm | = 12 cm |
![]() ii
ii![]()
![]() Also
Also 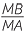 =
= 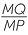
![]() (matching sides of similar triangles)
(matching sides of similar triangles)
 |
=  |
|
| MB | = 9 ×  |
|
= 13 cm cm |
EXAMPLE
a![]() In each diagram below, complete the similarity statement ‘ABC is similar to…’, stating the similarity test used.
In each diagram below, complete the similarity statement ‘ABC is similar to…’, stating the similarity test used.
b![]() Hence find the length of AC in each case.
Hence find the length of AC in each case.
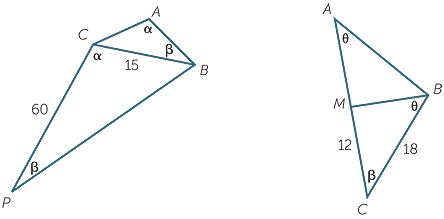
Solution
a![]()
 ABC is similar to
ABC is similar to  CPB (AAA similarity test)
CPB (AAA similarity test)
![]() nABC is similar to
nABC is similar to  BMC (AAA similarity test)
BMC (AAA similarity test)
b![]() We apply matching sides of similar triangles in both diagrams.
We apply matching sides of similar triangles in both diagrams.
| In the first diagram, | In the second diagram, | ||||
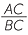 |
= 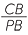 |
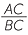 |
= 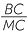 |
||
 |
= 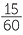 |
 |
= 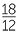 |
||
| AC | = 15 × 14 | AC | = 18 × 32 | ||
| = 334. | = 27. | ||||
Using the SAS similarity test
The first example below displays both ways of writing the ratio condition on the sides, first in the proof of similarity in part a, then in the subsequence calculation of a side length.
Part c shows how the equality of two angles can be used to prove that two lines are parallel.
Example
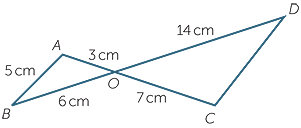 In the diagram to the right:
In the diagram to the right:
a![]() Prove that
Prove that  AOB is similar to
AOB is similar to  COD.
COD.
b![]() Find the length of CD.
Find the length of CD.
c![]() Prove that AB || DC.
Prove that AB || DC.
Solution
| a | In the triangles AOB and COD: | |||
 AOB = AOB =  COD COD |
(vertically opposite angles) | |||
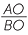 = =  (given) (given) |
or | 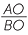 = =  |
||
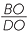 = =  (given) (given) |
 = =  |
|||
so  AOB is similar to AOB is similar to  COD (SAS similarity test). COD (SAS similarity test). |
||||
| b | 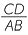 = = 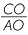 (matching sides of similar triangles) or (matching sides of similar triangles) or 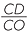 = = 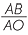 |
|||
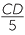 = =  |
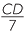 = =  |
|||
CD = 11 cm. cm. |
CD = 11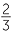 cm. cm. |
|||
| c |  A = A =  C (matching angles of similar triangles), so AB || DC (alternate angles are equal). C (matching angles of similar triangles), so AB || DC (alternate angles are equal). |
|||
The second method in parts a and b above compares lengths within each triangle.
Using the SSS similarity test
The following example shows how to use the SSS similarity test to prove that angles are equal.
Example
a![]() Prove that the two triangles in the diagram are similar.
Prove that the two triangles in the diagram are similar.
b![]() Which of the marked angles are equal?
Which of the marked angles are equal?
Solution
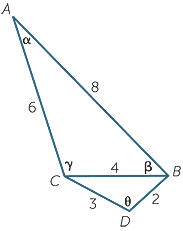 a
a![]() In the triangles ABC and CBD:
In the triangles ABC and CBD:
![]() AB = 2 × CB
AB = 2 × CB![]() (given)
(given)
![]() BC = 2 × BD (given)
BC = 2 × BD (given)
![]() CA = 2 × DC (given)
CA = 2 × DC (given)
so  ABC is similar to
ABC is similar to  CBD (SSS).
CBD (SSS).
b![]() Hence g = θ (matching angles of similar triangles).
Hence g = θ (matching angles of similar triangles).
Using the RHS similarity test
As with congruence, the SAS similarity test requires that the pair of equal angles be included between the pairs of sides that are in ratio. When the equal angles are right angles, however, we can use the RHS similarity test, in which the pair of equal angles are not included between the pairs of sides that are in ratio.
Example
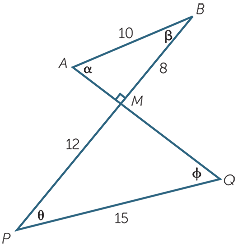 a
a![]() Prove that the two triangles in the diagram
Prove that the two triangles in the diagram ![]() to the right are similar.
to the right are similar.
b![]() Identify the equal angles in the two triangles.
Identify the equal angles in the two triangles.
c![]() Prove that AB || PQ.
Prove that AB || PQ.
Solution
a![]() In the triangles ABM and QPM:
In the triangles ABM and QPM:
![]()
 AMB =
AMB =  QMP = 90° (given)
QMP = 90° (given)
![]()
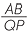 =
= 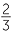 =
= 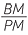 (given) or
(given) or 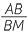 =
=  =
= 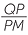
![]() so
so  ABM is similar to
ABM is similar to  QPM
QPM![]() (RHS similarity test).
(RHS similarity test).
b![]() Hence θ = β and f = α
Hence θ = β and f = α![]() (matching angles of similar triangles).
(matching angles of similar triangles).
c![]() Hence AB || PQ
Hence AB || PQ![]() (alternate angles are equal).
(alternate angles are equal).
We indicated above how the RHS similarity test can be developed from the RHS congruence test. It is also possible to use Pythagoras’ theorem to develop the RHS congruence test from the SSS congruence test. The following exercise gives the details.
Exercise 5
In the two right-angled triangles in the diagram,
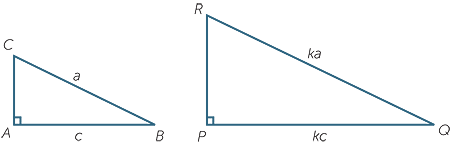
- the two hypotenuses are in the ratio 1 : k, and
- the sides AB and PQ are in the ratio 1 : k.
a![]() Show that PR = k
Show that PR = k![]() .
.
b![]() Hence show that
Hence show that  ABC is similar to
ABC is similar to  PQR.
PQR.
The similarity tests as generalisations of the congruence tests
Two figures are congruent when they are similar with similarity ratio 1 : 1. The four congruence tests can be regarded as special cases of the four similarity tests when the similarity ratio is 1 : 1.
For example, the SSS similarity test specifies that the matching sides of the two triangles are in a constant ratio, and the SSS congruence test specifies that the matching sides have equal length, that is, that the constant ratio is 1 : 1.
Similarly, the SAS and RHS similarity tests each specify that the ratios of the two pairs of matching sides are equal, and the SAS and RHS congruence tests each specify that the two pairs of matching sides have equal length, that is, that the constant ratio is 1 : 1.
The AAS congruence test requires that matching angles are equal, and that one pair of matching sides are equal. This is generalised by the AA congruence test, which only specifies that matching angles are equal − the ratio of any pair of matching sides is then the similarity ratio of the pair.
Similarity and intercept theorems
A point F on an interval AB divides the interval
into two subintervals AF and FB called intercepts. 
A point on a side of a triangle divides that side into two intercepts. Several important theorems about intercepts on the sides of triangles can be proven quickly using similarity.
The intercept theorem − A special case involving midpoints
We shall deal first with the special case involving the midpoints of two sides.
Theorem
The interval joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
Proof
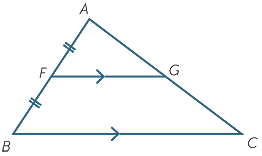
Let F and G be the midpoints of the sides AB and AC of  ABC.
ABC.
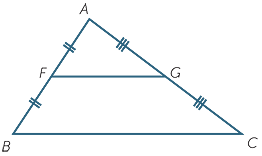 In the triangles AFG and ABC:
In the triangles AFG and ABC:
 FAG = FAG =  BAC BAC |
(common) | |
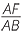 = = 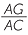 = =  |
(given) |
so  AFG is similar to
AFG is similar to  ABC (SAS similarity test).
ABC (SAS similarity test).
| Hence | BC | = 2 × FG | (matching sides of similar triangles). | |
| Also |  AFG AFG |
=  ABC ABC |
(matching angles of similar triangles), | |
| so | FG | || BC | (corresponding angles are equal). |
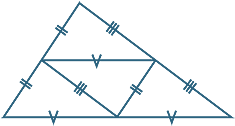 As a consequence of this theorem, if we join up the three midpoints of the sides of a triangle, as in the diagram on the right, we obtain four triangles that are congruent to each other by the SSS congruence test, each similar to the original triangle by the SAS similarity test.
As a consequence of this theorem, if we join up the three midpoints of the sides of a triangle, as in the diagram on the right, we obtain four triangles that are congruent to each other by the SSS congruence test, each similar to the original triangle by the SAS similarity test.
This dissection also demonstrates that each small triangle has one quarter the area of the large triangle.
The special case can also be proven using congruence alone, as in the following exercise, although the construction is a little more elaborate.
Exercise 6
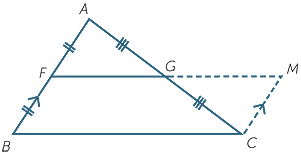 In the triangle ABC, F and G are the midpoints
In the triangle ABC, F and G are the midpoints
of AB and AC.
Construct the line through C parallel to BA,
and let it meet GF produced at M.
a![]() Prove that AFG × CMG.
Prove that AFG × CMG.
b![]() Prove that FG || BC.
Prove that FG || BC.
c![]() Prove that FG =
Prove that FG =  BC.
BC.
The midpoints of the sides of a quadrilateral
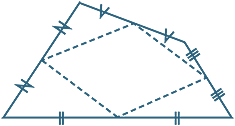 The intercept theorem for triangles has an interesting
The intercept theorem for triangles has an interesting
application to quadrilaterals. The midpoints of the sides
of any quadrilateral form a parallelogram, whose area
is half the area of the original quadrilateral.
This theorem is proven in the following exercise.
Exercise 7
In the diagram to the right, the points P, Q, R and S are the midpoints of the sides AB, BC, CD and DA respectively of a quadrilateral ABCD.
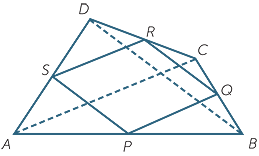 Join the diagonals AC and BD of the quadrilateral.
Join the diagonals AC and BD of the quadrilateral.
a![]() Show that PS || QR, and that PS = QR.
Show that PS || QR, and that PS = QR.
b![]() Show that PQ || SR, and that PQ = SR.
Show that PQ || SR, and that PQ = SR.
c![]() Show that area ASP =
Show that area ASP =  area ADB.
area ADB.
d![]() Show that area PQRS =
Show that area PQRS =  area ABCD.
area ABCD.
e![]() What conclusion can you draw about the diagonals of ABCD if:
What conclusion can you draw about the diagonals of ABCD if:
![]() i
i![]() PQRS is a rectangle?
PQRS is a rectangle? ![]() ii
ii![]() PQRS is a rhombus?
PQRS is a rhombus?
The intercept theorem − The general case
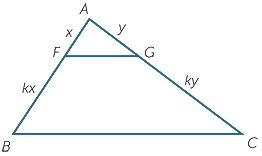 The intercept theorem as stated above is a special
The intercept theorem as stated above is a special
case − the points F and G can divide the sides AB
and AC in any given ratio.
Theorem
Let the points F and G divide the sides AB and AC of a triangle ABC in the same ratio 1 : k.
Then FG || BC and 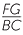 =
= 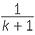 .
.
Proof
| Let AF = x and AG = y. | |||||
| Then FB = kx and GC = ky. | |||||
| In the triangles AFG and ABC. | |||||
 FAG = FAG =  BAC BAC |
(common) | ||||
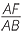 = = 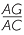 = = 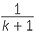 |
(given) | ||||
so  AFG is similar to AFG is similar to  ABC (SAS similarity test) with similarity ratio 1 : k + 1. ABC (SAS similarity test) with similarity ratio 1 : k + 1. |
|||||
| Hence | 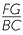 |
= 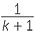 |
(matching sides of similar triangles). | ||
| Also |  AFG AFG |
=  ABC ABC |
(matching angles of similar triangles), | ||
| so | FG |
|| BC | (corresponding angles are equal). | ||
The converse of the intercept theorem for triangles −
A special case involving midpoints
The intercept theorem has an important converse. Again we shall deal first with the special case where F is the midpoint of the side AB.
Theorem
The interval from the midpoint of one side of a triangle parallel to a second side is half the length of the second side and bisects the third side.
Proof
 Let F be the midpoint of the side AB of ABC. Let the line through F parallel to BC meet AC at G.
Let F be the midpoint of the side AB of ABC. Let the line through F parallel to BC meet AC at G.
In the triangles AFG and ABC:
 FAG =
FAG =  BAC (common)
BAC (common)
 AFG =
AFG =  ABC (corresponding angles, FG || BC)
ABC (corresponding angles, FG || BC)
so AFG is similar to ABC (AAA similarity test).
Hence, using matching sides of similar triangles,
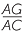 =
= 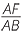 =
=  and
and 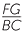 =
= 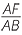 =
=  .
.
As before, this special case of the theorem does not actually require similarity.
It can be proven using congruence alone, as in the following exercise.
Exercise 8
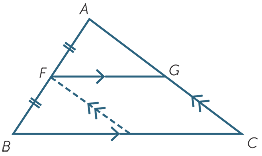 Construct E on BC so that FE || AC.
Construct E on BC so that FE || AC.
- a
- Prove that AFG
 FBE.
FBE. - b
- Prove that BE = FG = EC and that AG = FE = GC.
The converse of the intercept theorem − The general case
This special case can be generalised to apply to any line parallel to a side of a triangle.
Theorem
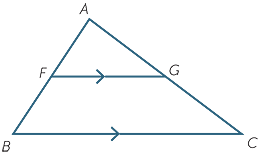 Let the point F divide the side AB of DABC in the ratio 1 : k.
Let the point F divide the side AB of DABC in the ratio 1 : k.
Let the line through F parallel to BC meet AC at G.
Then
![]()
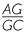 =
=  and
and 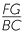 =
= 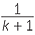 .
.
Proof
| In the triangles AFG and ABC: | ||||
 FAG = FAG =  BAC BAC |
||||
 AFG = AFG =  ABC ABC |
||||
so  AFG is similar to AFG is similar to  ABC (AAA similarity test). ABC (AAA similarity test). |
||||
| We know that | =  , , |
|||
| that is, | = 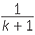 |
|||
| so | = 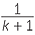 |
|||
| Also | = 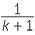 |
|||
| so | =  . . |
|||
The ratio of areas of similar triangles
We saw above that when two triangles are similar with similarity factor 2, then their areas are in the ratio 1 : 4. This is a special case of a more general result.
Theorem
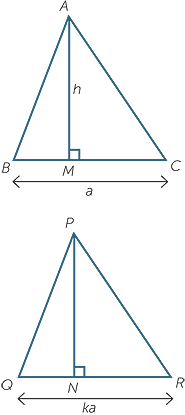 If two triangles are similar with similarity factor k,
If two triangles are similar with similarity factor k,
then their areas are in the ratio 1 : k2.
Proof
| Let ABC be similar to PQR, and let BC = a and QR = ka. | |||
| Let AM and PN be altitudes of the two triangles, and let AM = h. | |||
| Then PN = kh (matching lengths within similar triangles). | |||
| Hence area of PQR | =  × (ka) × (kh) × (ka) × (kh) |
||
= k2 ×  ah ah |
|||
= k2 × (area of  ABC). ABC). |
|||
Further applications of similarity
This section contains some further applications of similarity in geometry.
The altitude to the hypotenuse of a right-angled triangle
The altitude to the hypotenuse of a right-angled triangle divides the triangle into two triangles each similar to the original triangle. Several interesting results follow from this observation. The exercise below uses the construction to provide another proof of Pythagoras’ theorem, and then to prove these two further results:
Theorem
Let the altitude to the hypotenuse of a right-angled triangle divide the hypotenuse into two intercepts.
- a
- The square of the altitude equals the product of the intercepts.
- b
- The ratio of the squares of the other two sides equal the ratio of the intercepts.
Exercise 9
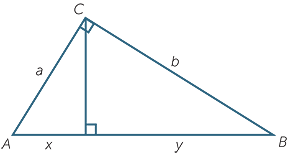 In the diagram to the right, CM is an altitude of the triangle ABC, which is right-angled at C.
In the diagram to the right, CM is an altitude of the triangle ABC, which is right-angled at C.
| a | Prove that all three triangles in the figure are similar, and write down the similarity statement. |
| b | Use the similarity of the left-hand triangle and the large triangle to prove that a2 = x2 + xy. |
c![]() Use a similar method to prove that b2 = y2 + xy.
Use a similar method to prove that b2 = y2 + xy.
d![]() Hence prove Pythagoras’ theorem by showing that a2 + b2 = (x + y)2.
Hence prove Pythagoras’ theorem by showing that a2 + b2 = (x + y)2.
e![]() Use the identities of parts b and c to prove that
Use the identities of parts b and c to prove that 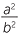 =
= 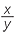
f![]() Use the similarity of the two smaller triangles to prove that h2 = xy.
Use the similarity of the two smaller triangles to prove that h2 = xy.
An enlargement construction
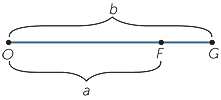 Suppose that we are given a centre of enlargement O
Suppose that we are given a centre of enlargement O
and asked to construct, using straight edge and compasses, an enlargement of some figure in the ratio
a : b, where a and b are the lengths of two given intervals OF and OG on a common ray OFG.
The following exercise shows how this can done.
Exercise 10
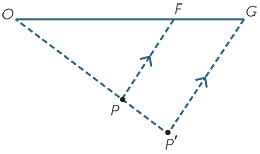 Let P be any point on the figure.
Let P be any point on the figure.
Join FP, then construct the line through G parallel to FP.
Let this line meet OP, produced if necessary, at P′.
Use similarity to prove that OP : OP′ = a : b.
The intercept theorem for three parallel lines
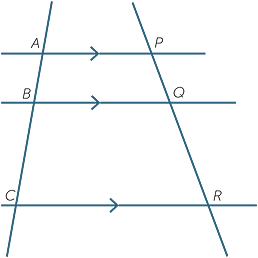 The intercept theorems have an interesting application to transversals of three parallel lines. The proof is presented in the following exercise.
The intercept theorems have an interesting application to transversals of three parallel lines. The proof is presented in the following exercise.
Theorem
When two transversals cross three parallel lines, the intercepts cut of one transversal are in the same ratio as the intercepts cut off the other transversal.
This means that in the diagram to the right,
AB : BC = PQ : QR.
Exercise 11
a![]() Prove the result when AC || PR.
Prove the result when AC || PR.
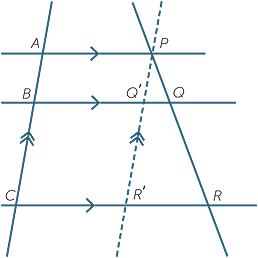 |
 |
||
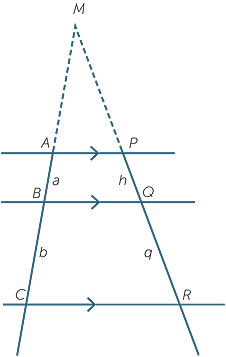
| b | Assume that AC is not parallel to PR, construct the line through P parallel to AC, and complete the proof. | c | Alternatively, assume again that AC is not parallel to PR, let AC meet PR at M, and complete the proof. |
Extension − The centroid of a triangle
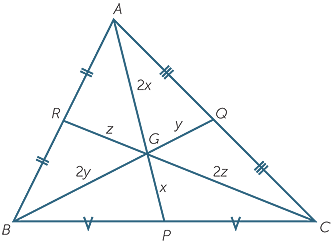 A median of a triangle is the interval joining the midpoint of a side to the opposite vertex. There are three medians in a triangle, and we can use the intercept theorem above to prove that they are concurrent in a point called the centroid
A median of a triangle is the interval joining the midpoint of a side to the opposite vertex. There are three medians in a triangle, and we can use the intercept theorem above to prove that they are concurrent in a point called the centroid
of the triangle. Moreover, the centroid trisects each median, or more precisely, divides it in the ratio 2 : 1.
Theorem
The medians AP, BQ and CR of a triangle ABC are concurrent at a point G called the centroid. The centroid trisects each median, in the sense that
![]() AG : GP = BG : GQ = CG : GR = 2 : 1.
AG : GP = BG : GQ = CG : GR = 2 : 1.
Exercise 12
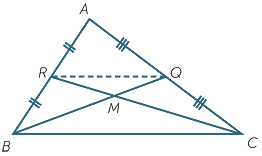
| a | Let the medians BQ and CR intersect at a point M. | |
| i | What does the intercept theorem for triangles tell us about the relationship between RQ and BC? | |
| ii | Prove that  BCM is similar to BCM is similar to  QRM. QRM. |
|
| iii | Hence prove that M divides BQ and CR in the ratio 2 : 1. | |
| b | Complete the proof of the theorem. | |
Extension − The golden mean and the diagonals of the regular pentagon
The five angles at the centre of a regular pentagon are each 360° ÷ 5 = 72°, so each interior angle of the pentagon is 54° + 54° = 108°.
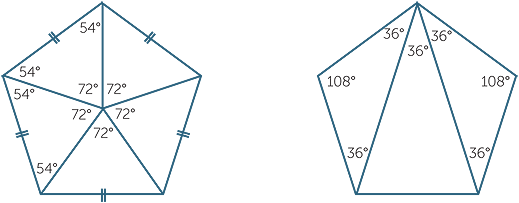
When we draw a diagonal, it forms an isosceles triangle with base angles 36° and 36°.
Thus at each vertex, the two diagonal trisect the vertex angle into three angles, each 36°.
Let ABCDE be a regular pentagon with side length 1, and join the diagonals AC, AD and BD.
Let AC meet BD at M, and let CM = x. Then by isosceles triangles, the lengths are as shown.

Exercise 13
- a
- Find the angles of
 ACD and
ACD and  DCM. Hence show that
DCM. Hence show that  ACD is similar to
ACD is similar to  DCM.
DCM. - b
- Hence show that
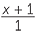 =
=  .
. - c
- By solving the quadratic equation, show that x =
 (
(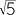 − 1).
− 1). - d
- Show that each diagonal has length
 (
(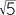 − 1).
− 1). - e
- The number f =
 (
(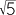 − 1) is called the golden mean. Use the identity in part b to prove that
− 1) is called the golden mean. Use the identity in part b to prove that
![]()
 = − 1.
= − 1.
Use the calculator to find an approximation for correct to three decimal places. Then verify this identity on your calculator.
Similarity is a useful tool in circle geometry, where equal angles turn up in what seem at first surprising positions. It is also more natural in circle geometry to express the theorems in terms of products of lengths than ratios of lengths. One example is worth giving in detail to illustrate the usefulness of similarity.
Theorem
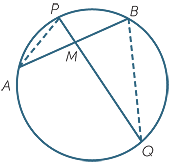 When two chords intersect within a circle,
When two chords intersect within a circle,
the products of the intercepts are equal.
Proof
Let AB and PQ be chords intersecting at M.
Join AP and BQ.
In the triangles APM and QBM:
1![]()
 PAM =
PAM =  BQM
BQM ![]() (angles on the same arc PB)
(angles on the same arc PB)
2![]()
 APM =
APM = QBM
QBM ![]() (angles on the same arc AQ)
(angles on the same arc AQ)
so  APM is similar to
APM is similar to  QBM (AAA similarity test).
QBM (AAA similarity test).
Hence![]()
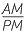 =
= 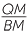
![]() (matching sides of similar triangles)
(matching sides of similar triangles)
so AM × BM = PM × QM.
Similarity is also useful in the study of the other conic sections − parabolas,
ellipses and hyperbolas.
The most important use of similarity in Years 9−10 mathematics, however, is in trigonometry, where similarity is required in the definitions of the trigonometric ratios. For example, we define
![]() sin 40° =
sin 40° = 
in a right-angled triangle with an angle of 40°. Such a definition requires the AAA similarity test to ensure that in any two such triangles, the ratio of the two sides is the same, no matter what the size of the triangle:

Because similarity is built into trigonometry, many geometric proofs using similarity also have an alternative trigonometric proof, where trigonometry can function as a sort of ‘automated similarity’, transferring ratios around the diagram. For example, here is an alternative proof of the intersecting chord theorem above. It uses trigonometry, in particular the sine rule, to transfer the ratio of the lengths.
Proof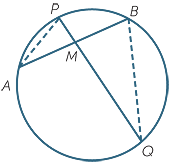
| In the triangles APM and QBM: | ||||||
 A A |
=  Q Q |
(angles on the same arc PB) | ||||
| and |  P P |
=  B B |
(angles on the same arc AQ), | |||
| so | 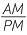 |
= 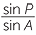 |
(sine rule in AMP) | |||
= 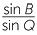 |
(proven above) | |||||
= 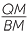 |
(sine rule in BMQ) | |||||
| so | AM × BM = PM × QM. | |||||
Similarity of other conic sections
We have already noted that any two circles are similar. The definition of the other conic sections in terms of focus and directrix and eccentricity means that
- any two parabolas are similar, and
- any two rectangular hyperbolas are similar.
To prove this, apply an enlargement to one conic so that the distance from focus to directrix is the same in its enlargement and in the other conic. The enlarged conic is then congruent to the other conic. More generally,
- any two ellipses with the same eccentricity are similar, and
- any two hyperbolas with the same eccentricity are similar.
Enlargements and other transformations
in coordinate geometry
Suppose that a figure in the coordinate plane is defined by an equation, and that an enlargement with centre the origin and similarity factor k is applied to the figure. The equation of the transformed figure can be found by replacing x by 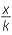 and y by
and y by 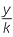 . For example, when the unit circle x2 + y2 = 1 is enlarged by a factor of 5, the equation of the enlarged figure is
. For example, when the unit circle x2 + y2 = 1 is enlarged by a factor of 5, the equation of the enlarged figure is
![]()
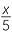 2 +
2 + 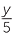 2 = 1
2 = 1
that is, ![]() x2 + y2 = 25.
x2 + y2 = 25.
There are many other important transformations in mathematics besides the four introduced so far. The study of functions uses dilations or stretchings, which enlarge a figure in one direction only, so that a circle becomes an ellipse. For example, when we stretch the unit circle x2 + y2 = 1 by a factor of 5 in the x-direction only, we replace x by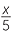 and obtain
and obtain
![]()
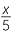 2 + y2 = 1
2 + y2 = 1
or equivalently, ![]() x2 + 25y2 = 25.
x2 + 25y2 = 25.
Another interesting transformation is a shear. For example, if we move every point
P(a, b) in the plane to the point P(a + kb, b) with the same height as P, but with x-coordinate increased by k times its y-coordinate, then a square with vertical and horizontal sides becomes a parallelogram.
In these last two situations, the resulting ellipse and parallelogram no longer have the same shape as the original figures. Nevertheless, they share important properties of the original − the diagonals of the parallelogram, for example, still bisect each other, and many theorems about tangents to circles have analogies in ellipses. A great deal of geometry investigates properties of figures that are preserved under various sets of transformations of them.
One can scarcely imagine a more useful piece of geometry than scale drawings.
Plans for buildings and other public works were prepared routinely in Roman times, and had already been used in slightly less systematic form at least by ancient Egyptian and Mesopotamian architects.
The notes in this module carefully talked about scale drawings of ‘the side of a train engine’ and ‘the facade of a cathedral’, so that all scale drawings were scale drawings of two-dimensional objects. The normal situation in architecture or engineering or biology, however, is scale drawings of three-dimensional objects. This can be done in various ways.
In architecture, the most obvious way to draw a plan for a building is to project the building onto a plane such as the ground, or onto a side wall. More complicated drawings project the build onto a slant plane, making it easier for the viewer to imagine a three-dimensional picture of the building.
Such projections are extremely useful for drawing up building plans, but they do not mimic the view of someone looking at the building. Whenever we see parallel lines with our eyes, they appear to meet at a point way off in the distance, and these considerations lead to the projective projections of buildings. Projective projections were made famous by painters in the Renaissance, but they are now used routinely in the computer programmes used by architects, who can invite viewers to take a virtual walk through a proposed building with the projection constantly changing as they go. Projective transformations also allow the various conic sections − circles, ellipses, parabolas and hyperbolas − to be transformed into each other.
Maps of anything larger than a small city need to take account of the curvature of the Earth when they represent the landscape on a two-dimensional map. A typical atlas will use various projections for different purposes, because each projection has its characteristic advantages and disadvantages.
Similarity
Similarity is an essential part of Greek geometry, and was used to great effect. An important theorem about cyclic quadrilaterals proven by the Egyptian mathematician Ptolemy (cAD90 − cAD 168) theorem shows how similarity can be used to prove surprising results about lengths and products of lengths. Its proof is given below in a structured exercise that is suitable as extension material.
Ptolemy’s theorem: The product of the diagonals of a cyclic quadrilateral equals the sum of the products of opposite sides.
Exercise 14
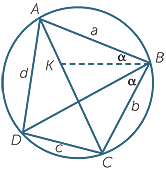 In the diagram to the right, ABCD is a cyclic quadrilateral
In the diagram to the right, ABCD is a cyclic quadrilateral
with sides AB = a, BC = b, CD = c and DA = d, with diagonals
AC = s and BD = t.
Construct K on AC with  ABK =
ABK =  CBD.
CBD.
- a
- Explain why
 BAC =
BAC =  BDC,
BDC,  ACB =
ACB =  ADB
ADB
and ABD =
ABD =  CBK.
CBK.
b![]() Show that
Show that  ABK is similar to
ABK is similar to  DBC, and hence show that AK × t = ac.
DBC, and hence show that AK × t = ac.
c![]() Show that
Show that  CBK is similar to
CBK is similar to  DBA, and hence show that CK × t = bd.
DBA, and hence show that CK × t = bd.
d![]() Hence show that st = ac + bd.
Hence show that st = ac + bd.
The converse of this theorem is also true, ‘If the product of the diagonals of a quadrilateral equals the sum of the products of opposite sides, then the quadrilateral is cyclic.’
Because the Greeks had no coherent theory of irrational numbers, there is always an uneasy relationship between similarity and the rest of Greek geometry. For example, one can construct with straight edge and compasses enlargements whose enlargement factor is any given rational number or square root of a rational number, but it is now known that one cannot construct an enlargement with enlargement factor 32 (the proof of this is not straightforward). This is the basis of one the three most famous unsolved problems passed on to the modern world by Greek mathematicians, ‘Given a cube, construct another cube of twice the volume.’ The problems of the relationships between the arithmetic of the real numbers and the geometry of the plane were only sorted out in the late 19th century.
The study of similarity is quite a challenge to students. The discussion in this module, using enlargement transformations to introduce similarity, was chosen because it makes good sense to students, and because it is well established in schools. It would be unwise to make the topic more complicated by introducing logical difficulties. Nevertheless, the preceding discussion has logical problems that some students begin asking questions about. For example:
- The four similarity tests can be proven from the congruence tests without enlargements when the similarity factor is a rational number.
- We never actually proved that enlargement transformations had the properties that we claimed they had, that is, that matching angles are equal and that matching lengths are in the same ratio. We only verified these properties in examples.
This appendix gives one of several possible approaches to dealing with these issues.
The first section, which essentially proves the AAA similarity test for positive rational values of k, may be suitable as Extension material for some students.
A. Equi-angular triangles in which two matching sidesk: 1
Let us then begin the whole discussion again, with neither similarity nor enlargements defined.
The first step is a theorem which essentially shows that the AAA similarity test holds when the similarity ratio k is a positive rational number. Because similarity has not yet been defined, the theorem is expressed not in terms of similarity, but as a test for the sides being in ratio.
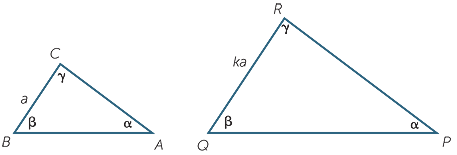
Theorem
Let ABC and PQR be equi-angular triangles, with  A =
A =  P = α,
P = α,  B =
B =  Q = β,
Q = β,  C =
C =  R = γ.
R = γ.
Let BC = α, CA = β and AB = c, and let QR = ka, where k is a positive rational number.
Then RP = kb and PQ = kc.
Proof
 First, we prove the result when k = 2.
First, we prove the result when k = 2.
Let F be the midpoint of QR. Then QF = FR = a.
Construct G on RP and H on QP so that
FG || QP and FH || RP. Omitting the details of the angle-chasing,  RFG
RFG 
 FQH (AAS congruence test).
FQH (AAS congruence test).
Using opposite sides of parallelograms and matching sides of congruent triangles,
HP = FG = QH and RG = FH = GP, as required.
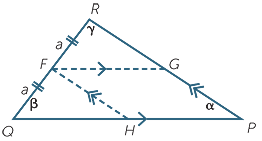
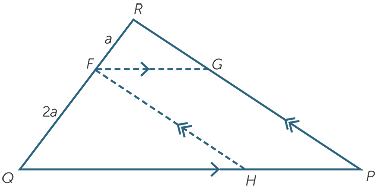 Secondly, we prove the result when k = 3. Let F divide RQ in the ratio 1 : 2. Then FR = a and FQ = 2a. Construct G on RP and H on QP so that FG || QP and FH || RP.
Secondly, we prove the result when k = 3. Let F divide RQ in the ratio 1 : 2. Then FR = a and FQ = 2a. Construct G on RP and H on QP so that FG || QP and FH || RP.
Omitting the details of the angle-chasing, RFG is similar to FQH (AAA similarity test with ratio 1 : 2).
Using opposite sides of parallelograms and matching sides of congruent triangles,
HP = FG =  QH and RG =
QH and RG =  FH =
FH =  GP, as required.
GP, as required.
Thirdly, to prove the result for all whole numbers k, each successive step uses the previous step and adapts the same argument. For example, the argument for k = 4 uses exactly the same argument as used for k = 3, except that the length FQ is now 3a.
Eventually the result can be proven for any whole number k. This method of successive argument for one whole number after the other will be formalised in Years 11−12 as mathematical induction.
Lastly, we have now outlined congruence proofs of the result for k = 2, 3, 4…. The test is therefore also proven for the reciprocal similarity factors k =  ,
, 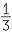 and
and  ,.... Then applying two tests in sequence, the test also follows for all fractions formed from the whole numbers, that is, for all rational numbers.
,.... Then applying two tests in sequence, the test also follows for all fractions formed from the whole numbers, that is, for all rational numbers.
Since every irrational number is ‘as close as we like’ to a rational number, it is reasonable to take as a new axiom of our geometry that the previous result holds for all positive real numbers.
- AAA: (A new axiom of geometry) If two triangles are equi-angular, then matching sides are in a constant ratio.
Using this axiom, we can now establish the other three tests in a form that still avoids the word ‘similarity’.
- SAS: If two triangles have a pair of equal angles, and the including sides are in a constant ratio, then the triangles are equi-angular and the third pair of sides are in the same ratio.
- SSS: If we can match up the sides of one triangle with the sides of another so that all the ratio of matching sides are the same, then the two triangles are equi-angular.
- RHS: If the ratio of the hypotenuse and one side of a right-angled triangle is equal to the ratio of the hypotenuse and one side of another right-angled triangle, then the two triangles are equi-angular and the third pair of sides are in the same ratio.
Here is a proof of the SAS test as stated above. In the two triangles below,
AB : PQ = AC : PR = 1 : k and  A =
A =  P.
P.
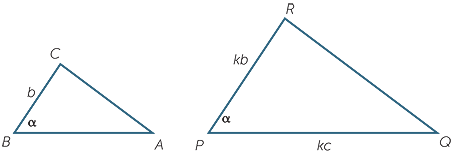
 Construct B′ on AB, produced if necessary,
Construct B′ on AB, produced if necessary,
so that AB′ = kc. Let the line through B′ parallel
to BC meet AC, produced if necessary, at C′.
| Then |  ABC ABC |
=  AB′C′ AB′C′ |
(corresponding angles, BC || B′C′) | ||
| so | AB′C′ |  PQR PQR |
by the AAS congruence test. |
Hence ABC and PQR are equi-angular, so using the new axiom introduced above,
![]()
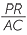 =
= 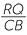 = k.
= k.
The other two tests can be proven with exactly analogous constructions.
The definition of enlargement given in this module is not really satisfactory as a geometric definition. It was based on constructing an interval that is k times a given interval, where k is any positive real number − such a construction cannot be done in general.
What we need is a definition of enlargement that is based not on a given real number k, but on the ratio of two given lengths. Such a construction was the subject of Exercise 10, and we now redefine enlargement to be the result of this construction.
This new definition of enlargement, together with the new axiom, will enable us to prove the properties of enlargements that could only be established by demonstration in the module.
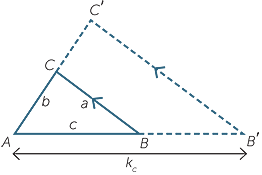
The enlargement transformation: Suppose that we are given a centre of enlargement O, and two intervals OF and OG of lengths a and b, lying on the same ray from O.
Define the enlargement with centre O and ratio a : b to be the transformation whose image of a point P in the plane is the point P′ as in the diagram to the right. That is, P′ is the intersection of OP, produced if necessary, with the line through G parallel to FP.
Using corresponding angles on parallel lines, the triangles OFP and OGP′ are equi-angular, so by the new axiom introduced in part B, it follows that
![]() OP : OP′ = a : b.
OP : OP′ = a : b.
The three properties of enlargements can now be proven.
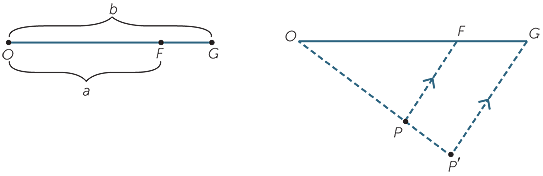
Theorem
When an enlargement with centre O and ratio OF : OG = a : b is applied.
a![]() AB : A′B′ = a : b, for each interval AB in the plane.
AB : A′B′ = a : b, for each interval AB in the plane.
b![]() AB || A′B′, for each interval AB in the plane.
AB || A′B′, for each interval AB in the plane.
c![]()
 ABC =
ABC =  A′B′C′, for each angle
A′B′C′, for each angle  ABC in the plane.
ABC in the plane.
Proof
- a
 Using the upper diagram to the right,
Using the upper diagram to the right,
we have shown above that
OA : OA′ = OB : OB′ = a : b. Hence using the SAS situation discussed in part B above, applied to OAB and OA′B′,
AB : A′B′ = a : b.- b
- Also

 OAB =
OAB =  OA′B′
OA′B′
so AB || A′B′.
AB || A′B′. - c
 Using the lower diagra m to the right,
Using the lower diagra m to the right,
we know from part b that AB || A′B′ and
BC || B′C′.Hence using corresponding angles,
 ABC =
ABC =  A′B′C′.
A′B′C′.
We can now define similarity exactly as before.
- Two figures are called similar if an enlargement of one is congruent to the other.
The theorem of part C now shows that two figures are similar when the points of one can be paired up with the points of the other so that matching angles are equal and matching sides are in the same ratio.
Exercise 1
| a | The height of the man on the photograph is about 5 mm. so the scale is about 5 mm : 2 m = 5 mm = 2000 mm = 1 : 400. |
|
| b | The height of each spire on the photograph is about 16.3 cm, so actual height ≈ 400 × 16.3 cm ≈ 65 metres. (The height of the actual church in Belgium is about 72 metres.) |
Exercise 3
| a | True. | |
| b | False. Any two rectangles whose sides are in the same ratio are similar. | |
| c | False. Any two rhombuses whose angles are equal are similar (or whose diagonals are in the same ratio). | |
| d | True. | |
| e | False. A sector of one circle is similar to a sector of another circle if the two sectors have the same angle at the centre. | |
| f | True. | |
| g | False. Any two isosceles triangles whose base angles are equal are similar (or whose sides are in the same ratio, or whose height and base are in the same ratio). |
Exercise 4
 Enlarge
Enlarge  ABC to
ABC to  A′B′C′ by a suitable enlargement
A′B′C′ by a suitable enlargement
factor so that A′B′ = PQ = kc.
Then B′C′ = ka and C′A′ = kb because the ratios of sides is preserved by enlargements.
Hence  A′B′C′ is congruent to
A′B′C′ is congruent to  PQR by the SSS congruence test, so ABC is similar to PQR,
PQR by the SSS congruence test, so ABC is similar to PQR,
because an enlargement of  ABC is congruence to
ABC is congruence to  PQR.
PQR.
Exercise 5
a![]() Using Pythagoras’ theorem in each triangle,
Using Pythagoras’ theorem in each triangle,
AC |
= k |
||
| and | PR | =  |
|
= k |
| b | Hence the sides AC and PR are in the same ratio 1 : k, so the two triangles are similar by the SSS simila rity test. |
Exercise 6
| a | In the triangles AFG and CMG: | ||||
| AG = CG | (given) | ||||
 AGF = AGF =  CGM CGM |
(vertically opposite angles) | ||||
 AFG = AFG =  CMG CMG |
(alternate angles, BA || CM) | ||||
| so AFG = CMG | (AAS congruence test) | ||||
| b | Hence CM | = AF | (matching sides of congruent triangles) | ||
| = BF | (given); | ||||
| so BCMF is a parallelogram, because a pair of opposite sides are equal and parallel. | |||||
| c | Hence | FM = BC | (opposite sides of parallelogram BCMF) | ||
| and | FG = MG | (matching sides of congruent triangles), | |||
| so | FG =  BC. BC. |
||||
Exercise 7
| a | Apply the intercept theorem to  ABD and ABD and  CBD, and combine the results. CBD, and combine the results. |
||||
| b | Apply the intercept theorem to  BAC and BAC and  DAC, and combine the results. DAC, and combine the results. |
||||
| c | Use the dissection immediately above this exercise. | ||||
| d | Using part c applied to all four outer triangles, | ||||
area  ASP + area ASP + area  CQR CQR |
=  area ABCD. area ABCD. |
||||
| and | area  BPQ + area BPQ + area  DRS DRS |
=  area ABCD. area ABCD. |
|||
Adding, sum of areas of four outer triangles =  area ABCD and subtracting, area ABCD and subtracting, area PQRS =  area ABCD. area ABCD. |
|||||
| e | i | The diagonals of ABCD are perpendicular. | |||
| ii | The diagonals of ABCD are equal. | ||||
Exercise 8
| a | Use the AAS congruence test. |
| b | Use matching sides of the congruent triangles AFG and FBE, and opposite sides of the parallelogram EFGC. |
Exercise 9
| a | Let  A = α. Then using adjacent angles and the angle sums of the triangles, A = α. Then using adjacent angles and the angle sums of the triangles,  ACM = 90° − α, ACM = 90° − α,  BCM = α, and BCM = α, and  B = 90° − α. B = 90° − α. |
||
Hence  ABC is similar to ABC is similar to  CBM is similar to ACM (AAA similarity test). CBM is similar to ACM (AAA similarity test). |
|||
| b |  |
=  |
(matching sides of similar triangles ACM and ABC) |
| a2 | = x(x + y) | ||
| = x2 + xy. | |||
| c |  |
= 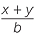 |
(matching sides of similar triangles CBM and ABC) |
| b2 | = y(x + y) | ||
| = xy + y2. | |||
| d | Adding the identities of parts b and c, a2 + b2 = x2 + xy + xy + y2 = (x + y)2. | ||
| e | Dividing the identities of parts b and c, | ||
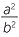 |
= 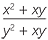 |
||
= 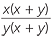 |
|||
= 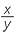 |
|||
| f | 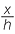 |
= 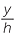 |
(matching sides of similar triangles CBM and ACM) |
| h2 | = xy. | ||
Exercise 10
In the triangles OFP and OGP′:
 FOP = FOP =  GOP′ GOP′ |
(common) | ||
 OFP = OFP =  OGP′ OGP′ |
(corresponding angles, FP || GP′) | ||
so  OFP is similar to OFP is similar to  OGP′ (AAA similarity test): OGP′ (AAA similarity test): |
|||
| Hence |  |
= 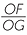 |
(matching sides of similar triangles) |
= 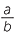 . . |
|||
Exercise 11
| a |
The opposite sides of both parallelograms are equal. | |||
| b | Let the line through P parallel to AC meet BQ at Q′, and CR at R′. | |||
| Then the opposites sides of the parallelograms ABQ′P and BCR′Q′ are equal, that is, | ||||
| PQ′ = AB and Q′R′ = BC. | ||||
Applying the intercept theorem for triangles to  QR′R, QR′R, |
||||
| PQ′ : Q′R′= PQ : QR |
||||
| so | AB : BC = PQ : QR. | |||
| c |
Let AB = a, BC = b, PQ = p and QR = q. | |||
Using the intercept theorem for triangles on  MBQ and on MBQ and on  MCR, MCR, |
||||
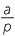 = =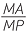 |
=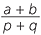 |
|||
| so ap + aq | = ap + bp | |||
| aq | = bp. | |||
Note: The working in part c assumed that the transversals meet outside the three parallel lines on the same side as A. There are, of course, three other cases to consider. What other cases should be considered in part b?
Exercise 12
- a
- i
- RQ || BC and RQ =
 BC.
BC. - ii
- In the triangles BCM and QRM:
 QMR =
QMR =  BMC
BMC (vertically opposite angles)
(vertically opposite angles)
 QRM =
QRM =  BCM
BCM (alternate angles, RQ || BC)
(alternate angles, RQ || BC) -
so
 BCM is similar to
BCM is similar to  QRM (AAA similarity test)
QRM (AAA similarity test) - BC = 2 × RQ
- iii
- Hence using matching sides of similar triangles,
MQ : MB = MR : MC = QR : BC = 1 : 2. - b
- We have now proven that any two medians of a triangle intersect in point that divides each median in the ratio 2 : 1.
Let G be the point that divides the median AP in the ratio 2 : 1. Then the other two medians BQ and CR pass through G, and G also divides these medians in the ratio 2 : 1.
Exercise 13
a ![]() Each triangle is isosceles with apex angle 72° and base angles 36°.
Each triangle is isosceles with apex angle 72° and base angles 36°.
b ![]()
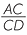 =
= 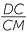 (matching sides of similar triangles)
(matching sides of similar triangles)
![]()
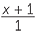 =
= 
c ![]() Hence x2 + x − 1 = 0
Hence x2 + x − 1 = 0
![]() x =
x = 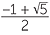 or
or 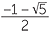 .
.
![]() Since x is positive, x =
Since x is positive, x =  (
(![]() − 1)
− 1)
| d | Hence AD | = x + 1 | |
=  ( ( |
e ![]() Substituting = x + 1 into the second line of part b gives φ − 1 =
Substituting = x + 1 into the second line of part b gives φ − 1 =  .
.
![]() From the calculator, φ ≈ 1:628, and
From the calculator, φ ≈ 1:628, and  ≈ 0.618 ≈ − 1
≈ 0.618 ≈ − 1
Exercise 14
a ![]() Use angles on the same arc, and adjacent angles at a point.
Use angles on the same arc, and adjacent angles at a point.
b ![]()
 ABK is similar to
ABK is similar to  DBC (AAA)
DBC (AAA)
![]() so
so 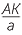 =
=  (matching sides of similar triangles)
(matching sides of similar triangles)
![]() AK × t = ac.
AK × t = ac.
c ![]()
 CBK is similar to
CBK is similar to  DBC (AAA)
DBC (AAA)
![]() so
so 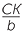 =
= 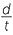 (matching sides of similar triangles)
(matching sides of similar triangles)
![]() CK × t = bd.
CK × t = bd.
d ![]() Adding the results of parts b and c,
Adding the results of parts b and c,
| (AK + CK) × t | = ac + bd | |
| st | = ac + bd. |
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

