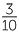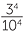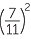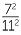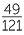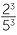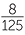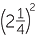The Improving Mathematics Education in Schools (TIMES) Project
Multiples, Factors and Powers
Number and Algebra : Module 19![]() Years : 7-8
Years : 7-8
June 2011
- Experience with the four operations of arithmetic.
- Instant recall of the multiplication table up to 12 × 12.
- Fractions and multiplication of fractions are required only for the last of the five index laws.
- No algebra is assumed in this module.
Multiplication and division of whole numbers throw up many surprising things. This module encourages multiplicative thinking about numbers, and introduces ideas that are essential skills in fractions and algebra.
The ideas of this module are presented in purely arithmetical form, and no algebra is used except in some remarks that look forward to later work. The only numbers in the module are whole numbers, apart from the final paragraphs, where fractions are used so that the fifth index law can be presented in a more satisfactory form.
Students first meet the distinction between odd numbers and even numbers in early primary school, but it is useful everywhere in mathematics. Even numbers are multiples of 2, and more generally, multiples arise throughout mathematics and everyday life. The mass of a stack of bricks is a multiple of the mass of one brick. The number of pages in a packet of notebooks is a multiple of the number of pages in one notebook.
The factors of a number can be displayed using rectangular arrays. Some numbers, such as 30, can arise in many different ways as a product,
![]() 30 = 1 × 30 = 2 × 15 = 3 × 10 = 5 × 6 = 2 × 3 × 5,
30 = 1 × 30 = 2 × 15 = 3 × 10 = 5 × 6 = 2 × 3 × 5,
whereas a number such as 31 can only be written trivially as the product 31 = 1 × 31. This idea leads to the classification of numbers greater than 1 as either prime or composite, and to a listing of all the factors of a number.
There are several groups of well-known divisibility tests that can check whether a number is a factor without actually performing the division. These tests greatly simplify the listing of factors of numbers.
Repeated addition leads to multiplication. Repeated multiplication in turn leads to powers, and manipulating powers in turn relies on five index laws. Powers are introduced in this module, together with four of the five index laws.
We are used to comparing numbers in terms of their size. The highest common factor (HCF) and lowest common multiple (LCM) allow us to compare numbers in terms of their factors and multiples. For example, when we look at 30 and 12, we see that they are both multiples of 6, and that 6 is the greatest factor common to both numbers. We also see that 60 is a multiple of both numbers, and that 60 is the lowest common multiple of them (apart from 0). The HCF and LCM are essential for fractions and later for algebra.
Here is the usual definition of odd and even whole numbers.
- A whole number is called even if it is a multiple of 2.
- A whole number is called odd if it is not even.
Thus 10 is even and 11 is odd. We can demonstrate this by writing
![]() 10 = 5 + 5
10 = 5 + 5 ![]() and
and ![]() 11 = 5 + 5 + 1,
11 = 5 + 5 + 1,
and we can illustrate this using arrays with two rows.
| |
 |
 |
|
10 = 5 + 5 |
11 = 5 + 5 + 1 |
The array representing the even number 10 has the dots divided evenly into two equal rows of 5, but the array representing the odd number 11 has an extra odd dot left over.
When we write out the whole numbers in order,

the even and odd numbers alternate, starting with 0, which is an even number because
0 + 0 = 0.
This pattern occurs in all sorts of common situations:
- When we walk, we step left, right, left, right,…
- When music is written in double time, like the Australian National Anthem, the notes are alternately stressed, unstressed, stressed, unstressed,…
- Our time is alternately divided day, night, day, night,…
- The squares on each row or column of a chessboard are alternately black, white, black, white,…
Indeed, our concept of the number 2 is so different from our conceptions of all other numbers that we even use different language. We divide a pie between two people, but among three people. We identify two alternatives, but three options. The word ‘doubt’ is related to the Latin ‘duo’, the word ‘two-faced’ means ‘liar’, and the traditional number of the devil is 2.
EXERCISE 1
Students often come up with other possible definitions of even whole numbers:
- Zero is even, and after that, odd and even numbers alternate.
- An even number can be written as the sum of two equal whole numbers.
- An even number has remainder 0 after division by 2.
What particular property of odd and even numbers does each illustrate?
Adding and subtracting odd and even numbers
There are several obvious facts about calculations with odd and even numbers that are very useful as an automatic check of calculations. First, addition and subtraction:
- The sum or difference of two odd numbers, or two even numbers, is even.
- The sum or difference of an odd number and an even number is odd.
Proofs by arrays usually convince students more than algebraic proofs. The diagram below illustrates ‘odd plus odd equals even’, and shows how everything depends on the odd dot left over. The other cases are very similar.
 +
+  =
= 
EXERCISE 2
Draw four diagrams to illustrate the four cases of subtraction of odd and even numbers.
Multiplication of odd and even numbers
When we multiply odd and even numbers,
- The product of an even number with any number is even.
- The product of two odd numbers is odd.
Proofs by arrays can be used here, but they are unwieldy. Instead, we will use the previous results for adding odd and even numbers. Here are examples of the three cases:
![]() 6 × 4 = 24,
6 × 4 = 24,![]() 5 × 4 = 20,
5 × 4 = 20,![]() 7 × 3 = 21.
7 × 3 = 21.
The first and second products are even because each can be written as the sum
of even numbers:
![]() 6 × 4 = 4 + 4 + 4 + 4 + 4 + 4
6 × 4 = 4 + 4 + 4 + 4 + 4 + 4![]() and
and![]() 5 × 4 = 4 + 4 + 4 + 4 + 4.
5 × 4 = 4 + 4 + 4 + 4 + 4.
The third product can be written as the sum of pairs of odd numbers, plus an extra
odd number:
![]() 7 × 3 = (3 + 3) + (3 + 3) + (3 + 3) + 3.
7 × 3 = (3 + 3) + (3 + 3) + (3 + 3) + 3.
Each bracket is even, because it is the sum of two odd numbers, so the whole sum is odd.
EXERCISE 3
What can we say about the quotients of odd and even numbers? Assuming in each case that the division has no remainder, complete each sentence below, if possible. Justify your answers by examples.
- a
- The quotient of an even number and an even number is…
- b
- The quotient of an even number and an odd number is…
- c
- The quotient of an odd number and an even number is…
- d
- The quotient of an odd number and an odd number is…
Using algebra for odd and even numbers
The previous results on the arithmetic of odd and even numbers can be obtained later after pronumerals have been introduced, and expansions of brackets and taking out a common factor dealt with. The important first step is:
- Any even number can be written as 2a, where a is a whole number.
- Any odd number can be written as 2a + 1, where a is a whole number.
EXERCISE 4
Obtain the previous results on the addition and multiplication of odd and even numbers by algebra. Begin, ‘Let the even numbers be 2a and 2b, and the odd numbers be 2a + 1 and 2b + 1, where a and b are whole numbers.’
Representing numbers by arrays
In the previous section, we represented even numbers by arrays with two equal rows, and odd numbers by arrays with two rows in which one row has one more dot than the other.
Representing numbers by arrays is an excellent way to illustrate some of their properties. For example, the arrays below illustrate significant properties of the numbers 10, 9, 8 and 7.
The number 10
There are two rectangular arrays for 10:
 |
 |
||
|
10 = 2 × 5 |
10 = 1 × 10 |
The first array shows that 10 can be factored as 10 = 5 × 2, which means that 10 is an even number.
The second array is trivial − every number can be factored as a product of itself and 1.
The convention used in these modules is that the first factor represents the number of rows, and the second factor represents the number of columns. The opposite convention, however, would be equally acceptable.
The number 9
The number 9 also has two rectangular arrays:
 |
 |
||
|
9 = 3 × 3 |
9 = 1 × 9 |
The first array shows that 9 is a square because it can be represented as a square array. The corresponding factoring is 9 = 3 × 3.
Because there is no 2-row array, the number 9 is odd. The second array is the trivial array.
The number 8
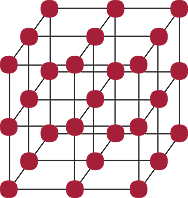
The number 8 has two rectangular arrays and a three-dimensional array:
 |
 |
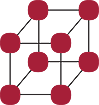 |
|||
|
8 = 2 × 4 |
8 = 1 × 8 |
8 = 2 × 2 × 2 |
The third array shows that 8 is a cube because it can be represented as a cubic array.
The corresponding factoring is 8 = 2 × 2 × 2.
The first array shows that 8 is even, and the second array is the trivial array.
The number 7
The interesting thing about the number 7 is that it only has the trivial array, because 7 dots cannot be arranged in any rectangular array apart from a trivial array.
![]()

![]() 7 = 1 × 7
7 = 1 × 7
Numbers greater than 1 with only a trivial rectangular array are called prime numbers. All other whole numbers greater than 1 are called composite numbers.
We shall discuss prime numbers in a great deal more detail in the later module, Primes and Prime Factorisation. The usual definition of a prime number expresses exactly the same thing in terms of factors:
- A prime number is a whole number greater than 1 whose only factors are itself and 1.
- A composite number is a whole number greater than 1 that is not a prime number.
Here are the only possible rectangular arrays for the first four prime numbers:
 |
 |
 |
 |
||||
|
2 |
3 |
5 |
7 |
Exercise 5
- a
- Draw all possible rectangular arrays for the numbers from 1 to 12, including any three dimensional arrays, and identify the corresponding factorings. Which of these numbers are prime, which are composite, which are square, and which are even?
- b
- List all the prime numbers less than 50. How many of these are even?
- c
- Identify all two-dimensional and three-dimensional arrays for 36.
- d
- Draw all rectangular arrays for 16, including three-dimensional arrays.
- e
- If you had four dimensions at your disposal, what array would you draw?
- f
- What is the smallest number greater than 1 that is both square and cubic?
What are the side lengths of the corresponding arrays? - g
- Why is a manufacturer more likely to pack his goods in packets of 30 than in packets of 29 or 31?
EXERCISE 6
- a
- Prove that when the diagonal of a square array is removed, the number of remaining dots is even.
- b
- If a number is subtracted from its square, what sort of number remains?
EXERCISE 7
- a
- Prove that in any square array, the number of dots on the outside of the array
is a multiple of 4. - b
- Hence prove that the difference of two even squares is divisible by 4, and that the difference of two odd squares is divisible by 4.
Rectangular arrays are not the only way that numbers can usefully be represented by patterns of dots.
- A triangular number is a number that can be represented as a triangular array, in which each row has one more dot than the row above.
 |
 |
 |
 |
||||||
|
1 |
1 + 2 = 3 |
1 + 2 + 3 = 6 |
1 + 2 + 3 + 4 = 10 |
1 + 2 + 3 + 4 + 5 = 15 |
Thus the first few triangular numbers are: 1, 3, 6, 10, 15, 21,…
EXERCISE 8
- a
- Explain the pattern of differences between successive triangular numbers.
- b
- Hence write down the first 20 triangular numbers.
- c
- Identify and explain the pattern of odd and even numbers in this sequence.
EXERCISE 9
 In the diagram to the right, two copies of the fourth triangular number have been fitted together to make a rectangle.
In the diagram to the right, two copies of the fourth triangular number have been fitted together to make a rectangle.
Explain how to calculate from this diagram that the 4th triangular number is 10. Hence calculate the 100th triangular number.
Multiples, common multiples and the LCM
- A multiple of a number such as 6 is a product of 6 and any whole number.
We can arrange the multiples of 6 in increasing order,
![]() 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96,…
0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96,…
so that they form a simple pattern increasing by 6 at each step.
Because 6 is an even number, all its multiples are even. The multiples of an odd number such as 7, however, alternate even, odd, even, odd, even,… because we are adding the odd number 7 at each step.
![]()

The number zero is a multiple of every number. Because of this, the word ‘multiple’ is sometimes used in the sense of ‘nonzero multiple’, but we will always add the word ‘nonzero’ when 0 is excluded.
The multiples of zero are all zero. Every other whole number has infinitely many multiples. This phrase ‘infinitely many’ has a very precise meaning — however many multiples you write down, there is always another multiple that you haven’t written down.
We can illustrate the multiples of a number using arrays with three columns and an increasing numbers of rows. Here are the first few multiples of 3:
 |
 |
 |
 |
 |
 |
||||||||
| |
0 |
|
3 |
|
6 |
|
9 |
|
12 |
|
15 |
|
18 |
Rows and columns can be exchanged. Thus the multiples of 3 could also be illustrated using arrays with three rows and an increasing numbers of columns.
Division
The repeating pattern of common multiples is a great help in understanding division.
Here again are the multiples of 6,
![]() 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96,…
0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96,…
If we divide any of these multiples by 6, we get a quotient with remainder zero.
For example,
![]() 24 ÷ 6 = 4
24 ÷ 6 = 4![]() and
and![]() 30 ÷ 6 = 5.
30 ÷ 6 = 5.
To divide any other number such as 29 by 6, we first locate 29 between two multiples of 6. Thus we locate 29 between 24 and 30. Because 29 = 24 + 5, we write
![]() 29 ÷ 6 = 4 remainder 5
29 ÷ 6 = 4 remainder 5 ![]() or alternatively
or alternatively ![]() 29 = 6 × 4 + 5.
29 = 6 × 4 + 5.
Notice that the remainder is always a whole number less than 6, because the multiples of 6 step up by 6 each time. Hence with division by 6 there are only 6 possible remainders,
![]() 0, 1, 2, 3, 4, 5.
0, 1, 2, 3, 4, 5.
This result takes a very simple form when we divide by 2, because the only possible remainders are 0 and 1.
- An even number has remainder 0 after division by 2.
- An odd number has remainder 1 after division by 2.
In later years, when students have become far more confident with algebra, these remarks about division can be written down very precisely in what is called the division algorithm.
- Given a whole number n (the dividend) and a nonzero whole number d (the divisor), there are unique whole numbers q (the quotient) and r (the remainder) so that:
n = dq + r and 0 £ r < d.
For example, we saw that 29 ÷ 6 = 4 remainder 5 means that
![]() 29 = 6 × 4 + 5
29 = 6 × 4 + 5 ![]() and
and ![]() 0 £ 5 < 6.
0 £ 5 < 6.
EXERCISE 10
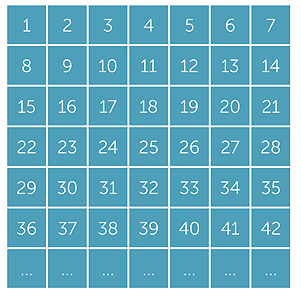
The table above shows all the whole numbers written out systematically in 7 columns. Suppose that each number in the table is divided by 7 to produced a quotient and
a remainder.
- a
- What is the same about the results of the division in each row?
- b
- What is the same about the results of the division in each column?
EXERCISE 11
When 22 and 41 are divided by 6, their remainders are 4 and 5 respectively. Yet when their sum 63 is divided by 6, the remainder is 3, and is not 4 + 5 = 9. Explain.
Common multiples and the LCM
An important way to compare two numbers is to compare their lists of multiples. Let us write out the first few multiples of 4, and the first few multiples of 6, and compare the two lists.
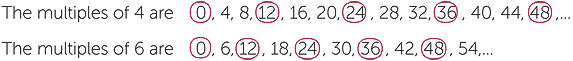
The numbers that occur on both lists have been circled, and are called common multiples.
The common multiples of 6 and 8 are 0, 12, 24, 36, 48,…
Apart from zero, which is a common multiple of any two numbers, the lowest common multiple of 4 and 6 is 12.
These same procedures can be done with any set of two or more non-zero whole numbers.
- A common multiple of two or more nonzero whole numbers is a whole number that a multiple of all of them.
- The lowest common multiple or LCM of two or more whole numbers is the smallest of their common multiples, apart from zero.
EXAMPLE
- a
- Write out the first few common multiples of 12 and of 16. Hence write out the first few common multiples of 12 and 16, and state their lowest common multiple.
- b
- Write out the first few multiples of 24. Hence write down the LCM of 12, 16 and 24?
- c
- What is the LCM of 12 and 15?
- d
- What is the LCM of 4, 6 and 9?
Solution
- a
- The multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144,…
The multiples of 16 are 16, 32, 48, 64, 80, 96, 112, 128, 144, 160,…
Hence the common multiples of 12 and 16 are 48, 96, 144,… and their LCM is 48. - b
- The multiples of 24 are 0, 24, 48,… Hence the LCM of 12, 16 and 24 is 48.
- c
- The LCM of 12 and 15 is 60.
- d
- The LCM of 4, 6 and 9 is 36.
Two or more nonzero numbers always have a common multiple — just multiply the numbers together. But the product of the numbers is not necessarily their lowest common multiple. For example, in the case above of 4 and 6, one common multiple is 4 × 6 = 24, but their lowest common multiple is 12.
EXAMPLE
- a
- What is the LCM of 9 and 10?
- b
- What is the LCM of the first five primes?
- c
- What is the LCM of 6 and 24? What is the general situation illustrated here?
- d
- What is the LCM of 1 and 14? What is the general situation illustrated here?
Solution
- a
- The LCM of 9 and 10 is their product 90.
- b
- The LCM of 2, 3, 5, 7 and 11 is their product, which is 2310.
- c
- Because 24 is a multiple of 6, the LCM of 6 and 24 is 24.
- d
- Every number is a multiple of 1, so the LCM of 1 and 14 is 14.
The common multiples are the multiples of the LCM
You will have noticed that the list of common multiples of 4 and 6 is actually a list of multiples of their LCM 12. Similarly, the list of common multiples of 12 and 16 is a list of the multiples of their LCM 48.
This is a general result, which in Year 7 is best demonstrated by examples. In an exercise at the end of the module, Primes and Prime Factorisation, however, we have indicated how to prove the result using prime factorisation.
We will have more to say about the LCM once the HCF has been introduced.
Factors, common factors and the HCF
- We say that 6 is a factor of 18 because 18 can be factored as the product 18 = 6 × 3.
This can be restated in terms of the multiples of the previous section:
- The statement that ‘6 is a factor of 18’ means that ‘18 is a multiple of 6.’
The number zero is a multiple of every number, so every number is a factor of zero. On the other hand, zero is the only multiple of zero, so zero is a factor of no numbers except zero. These rather odd remarks are better left unsaid, unless students insist. They should certainly not become a distraction from the nonzero whole numbers that we want to discuss.
The product of two nonzero whole numbers is always greater than or equal to each factor in the product. Hence the factors of a nonzero number like 12 are all less than or equal to 12. Thus whereas a positive whole number has infinitely many multiples, it has only finitely many factors.
The long way to find all the factors of 12 is to test systematically all the whole numbers less than 12 to see whether or not they go into 12 without remainder. The list of factors of 12 is
![]() 1, 2, 3, 4, 6 and 12.
1, 2, 3, 4, 6 and 12.
It is very easy to overlook factors by this method, however. A far more efficient way, is to look for pairs of factors whose product is 12. Begin by testing all the whole numbers 1, 2, … that could be the smaller of a pair of factors with product 12,
![]() 1, 2, 3,…
1, 2, 3,…
We stop at 3 because 42 = 16 is greater than 12, so 4 cannot be the smaller of a pair.
Now we add, in reverse order, the complementary factor of each pair, that is, 12 ÷ 3 = 4, 12 ÷ 2 = 6 and 12 ÷ 1 = 12,
![]()
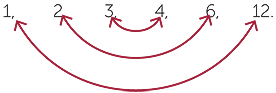
We can display these pairs of factors by writing the 12 dots in all possible rectangular arrays:
 |
 |
 |
|||
| |
1 × 12 |
|
2 × 6 |
|
3 × 4 |
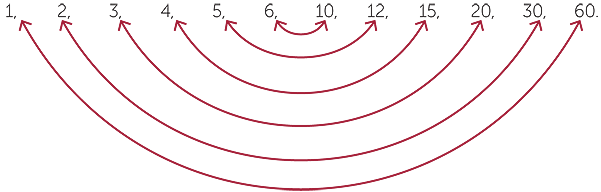
For a larger number such as 60, the method recommended here has the following steps:
- Test whether each whole number 1, 2, 3,… is a factor of 60.
- Continue testing up to 7, because 82 = 64 is greater than 60.
- Then write down each complementary factor in reverse order.
Thus the factors of 60 are
![]()
EXERCISE 12
Use this method to write down all the factors of 72 and 160.
Common factors and the HCF
Another important way to compare two numbers is to compare their lists of factors.
Let us write out the lists of factors of 18 and 30, and compare the lists.

The numbers that occur on both lists have been circled, and are called the common factors.
The common factors of 18 and 30 are 1, 2, 3 and 6.
The highest common factor is 6.
As with common multiples, these procedures can be done with any list of two or more whole numbers.
- A common factor of two or more whole numbers is a whole number that is a factor of all of them.
- The highest common factor or HCF of two or more whole numbers is the largest of these common factors.
The HCF is also known as the ‘greatest common divisor’, with corresponding initials GCD.
EXAMPLE
- a
- Write out the factors of 30 and of 75. Hence write out the common factors
of 30 and 75, and their highest common factor. - b
- Write out the factors of 45. Hence write down the HCF of 30, 75 and 45.
- c
- What is the HCF of 60, 80, 90 and 100?
- d
- What is the HCF of 82 and 102?
Solution
- a
- The factors of 30 are 1, 30, 2, 15, 3, 10, 5, 6.
The factors of 75 are 1, 75, 3, 25, 5, 15.
Hence the common factors of 30 and 75 are 1, 3, 5, 15, and their HCF is 15. - b
- The factors of 45 are 1, 3, 5, 9, 15, 45.
- c
- Hence the HCF of 30, 75 and 45 is 15.
- d
- The HCF of 60, 80, 90 and 100 is 10.
- e
- The HCF of 82 and 102 is 22.
Any collection of whole numbers always has 1 as a common factor. The question is whether the numbers have common factors greater than 1.
Every whole number is a factor of 0, so the common factors of 0 and say 12 are just the factors of 12, and the HCF of 0 and 12 is 12. A nonzero whole number has only a finite number of factors, so it has a greatest factor. Two or more numbers always have a HCF because at least one of them is nonzero. These are distractions from the main ideas.
EXAMPLE
- a
- What is the HCF of 6 and 24? What is the general situation illustrated here?
- b
- What is the HCF of 1 and 14? What is the general situation illustrated here?
- c
- What is the HCF of 21 and 10? Find three other pairs of composite numbers with the same HCF.
- d
- What is the HCF of 0 and 15?
Solution
- a
- Because 6 is a factor of 24, the HCF of 6 and 24 is 6.
- b
- The only factor of 1 is 1, so the HCF of 1 and 14 is 1.
- c
- The HCF of 21 and 10 is 1. Some other pairs of composite numbers with HCF 1 are 4 & 9, 16 & 25, 22 & 35, 14 & 15, 12 & 55.
- d
- All the factors of 15 are also factors of 0, so the HCF of 0 and 15 is 15.
The common factors are the factors of the HCF
You will have noticed that the list of common factors of 18 and 30 is actually a list of factors of their HCF 6. Similarly, the list of common factors of 30 and 75 is a list of the factors of their HCF 15.
Again, this is a general result, which in Year 7 is best demonstrated by examples. An exercise at the end of the module Primes and Prime Factorisation indicates how to prove the result using prime factorisation.
Two relationships between the HCF and LCM
The two relationships below between the HCF and the LCM are again best illustrated by examples in Year 7, but an exercise in the module Primes and Prime Factorisation indicates how they can be proven.
The first relationship is extremely useful, and is used routinely when working with common denominators of fractions.
- If the HCF of two numbers is 1, then their LCM is their product.
The converse is also true, although it does not arise so often.
For example,
The numbers 4 and 9 have HCF 1, and their LCM is their product 36.
The numbers 6 and 7 have HCF 1 and their LCM is their product 42.
EXAMPLE
- a
- Find the HCF and LCM of 21 and 10.
- b
- Find the HCF and LCM of 14 and 15.
Solution
- a
- The HCF of 21 and 10 is 1, and their LCM is their product 210.
- b
- The HCF of 28 and 15 is 1, and their LCM is their product 420.
The second relationship is not so obvious, and needs to be brought out by examples.
- The product of the HCF and LCM of two nonzero whole numbers is the product of the numbers.
For example, the numbers 4 and 6 have HCF 2 and LCM 12, and 2 × 12 = 4 × 6.
EXAMPLE
Confirm this relationship for:
a![]() 10 and 15
10 and 15 ![]() b
b![]() 12 and 9
12 and 9 ![]() c
c![]() 40 and 10
40 and 10
Solution
- a
- The numbers 10 and 15 have HCF 5 and LCM 30, and 10 × 15 = 5 × 30.
- b
- The numbers 12 and 9 have HCF 3 and LCM 36, and 12 × 9 = 3 × 36.
- c
- The numbers 40 and 10 have HCF 10 and LCM 40, and 10 × 40 = 40 × 10.
The three-part example below indicates how this relationship can be proven from the relationship above, although such a proof would be unsuited for most Year 7 students.
EXERCISE 13
- a
- Find the HCF and LCM of 12 and 20, and show that LCM × HCF = 12 × 20.
- b
- Show that when 12 and 20 are each divided by their HCF, the HCF of the resulting numbers is 1.
- c
- Show that when the LCM is divided by 12 and by 20, the HCF of the resulting
numbers is 1.
When we multiply a number by itself, we usually use a more concise notation,
| 3 = 31 | |||
| 3 × 3 = 32 | (read as ‘3 squared’) | ||
| 3 × 3 × 3 = 33 | (read as ‘3 cubed’) | ||
| 3 × 3 × 3 × 3 = 34 | (read as ‘3 to the power 4’ or as ‘3 to the 4th’) | ||
| 3 × 3 × 3 × 3 × 3 = 35 | |||
| 3 × 3 × 3 × 3 × 3 × 3 = 36 |
- The expression 35 is called a power of 3.
- The raised 5 in 35 is called the index of the power.
- The number 3 in 35 is called the base of the power.
The terms ‘3 squared’ for 32 and ‘3 cubed’ for 33 come from geometry. As we saw earlier in the module, we can arrange 32 dots in a square and 33 dots in a cube:
 |
 |
||
| 32 | 33 |
- The numbers 02 = 0, 12 = 1, 22 = 4, 32 = 9… are called squares.
- The numbers 03 = 0, 13 = 1, 23 = 8, 33 = 27… are called cubes.
As mentioned before, there is no straightforward geometrical representation of
higher powers.
Exercise 14
- a
- Write down the first 16 squares, starting from 02 = 0.
- b
- Write down the first 13 cubes, starting from 03 = 0.
Exercise 15
- a
- What is the smallest number that can be written as the sum of two squares in two distinct ways?
- b
- What is the smallest number that can be written as the sum of two nonzero squares
in two distinct ways? - c
- What is the smallest number that can be written as the sum of two distinct nonzero squares in two distinct ways?
- d
- The number 1729 is the smallest number that can be written as the sum of two cubes in two distinct ways. Show how this can be done. (This observation has become famous because of a conversation between the Indian mathematician Ramanujan and the English mathematician Hardy. See Wikipedia for the details.)
Exercise 16
Adding successive odd numbers gives successive squares:
| 1 = 1 | |
| 1 + 3 = 4 | |
| 1 + 3 + 5 = 9 | |
| 1 + 3 + 5 + 7 = 16 | |
| 1 + 3 + 5 + 7 + 9 = 25 | |
| 1 + 3 + 5 + 7 + 9 + 11 = 36 | |
| … |
Dissect a square array of 25 dots to show why this is happening.
Exercise 17
[A rather difficult challenge activity] Adding successive cubes gives the squares of the triangular numbers:
| 13 | = 1 | = 12 | ||
| 13 + 23 | = 9 | = 32 | ||
| 13 + 23 + 33 | = 36 | = 62 | ||
| 13 + 23 + 33 + 43 | = 100 | = 102 | ||
| 13 + 23 + 33 + 43 + 53 | = 225 | = 152 |
- a
- Gather a large number of small blocks, and build cubic stacks of 13 blocks, 23 blocks, 33 blocks,…
- b
- Place the stack of 13 = 1 blocks on the table, then dismantle the 23 = 8 stack and reassemble it systematically around the 13 = 1 stack to produce a square 3 × 3 array.
- c
- Dismantle the 33 = 27 stack and reassemble it systematically around the 3 × 3 array to produce a square 6 × 6 array.
- d
- Explain how the pattern continues to work.
Successive powers of a number
Powers of numbers are used extensively later in the study of logarithms and of combinatorics. It is useful to be able to compute or remember some smaller powers quickly, and recognise them.
The powers of 2 are: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192,…
The powers of 3 are: 3, 9, 27, 81, 243, 729,…
The powers of 4 are every second power of 2.
The powers of 5 are: 5, 25, 125, 625, 3125,…
The powers of 6 are: 6, 36, 216,…
The powers of 7 are: 7, 49, 343,…
The powers of 8 are every third power of 2.
The powers of 9 are every second power of 3.
The powers of 10 are: 10, 100, 1000, 10 000, 100 000, 1 000 000,…
The powers of 16 are every fourth power of 2.
Our base 10 place-value system displays every number as a sum of multiples of powers of 10.
Computers use a base 2 place-value system, so computer programmers need to know the powers of 2, and must be able to convert numbers quickly to a sum of powers of 2.
Exercise 18
Write 201 as a sum of powers of 2. Hence write 201 in base 2 notation.
There are several straightforward tests for divisibility that are very useful when factoring numbers. They all have their origin in the base 10 that we use for our system of numerals.
Divisibility by powers of 2 and powers of 5
The tests for divisibility by powers of 2 and 5 arise from the fact that 10 = 2 × 5.
Because 10 is a multiple of 2, every multiple of 10 is a multiple of 2. Thus to test whether a number is divisible by 2, we only need to look at the last digit.
- A number is divisible by 2 if its last digit is 0, 2, 4, 6 or 8.
Similarly, 10 is a multiple of 5, so every multiple of 10 is a multiple of 5. Thus to test whether a number is divisible by 5, we only need to look at the last digit.
- A number is divisible by 5 if its last digit is 0 or 5.
For example:
The number 864 ends with 4, so it is divisible by 2, but not by 5.
The number 1395 ends with 5, so it is divisible by 5, but not by 2.
The number 74 830 ends with 0, so it is divisible both by 2 and by 5.
The squares 22 = 4 and 52 = 25 are factors of 100, so every multiple of 100 is a multiple of 4 and of 25. Thus to test for divisibility by 4 and 25, we only need to look at the last two digits.
- A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
- A number is divisible by 25 if the number formed by its last two digits is divisible by 25.
Similarly, 23 = 8 and 53 = 125 are factors of 1000, so
- A number is divisible by 8 if the number formed by its last three digits is divisible by 8.
- A number is divisible by 125 if the number formed by its last three digits is divisible by 125.
These tests can be continued for higher powers of 2 and 5.
Example
- a
- Test 6 945 732 for divisibility by 2, 4, 8,…
- b
- Test 5 671 625 for divisibility by 5, 25, 125,…
Solution
- a
- The number 6 945 732 is divisible by 4 (and hence also by 2) because 32 is divisible by 4, but it is not divisible by 8 because 732 is not divisible by 8.
- b
- The number 5 671 625 is divisible by 125 (and hence also by 25 and 5) because 625 is divisible by 125, but it is not divisible by 54 = 625 because 1625 is not divisible by 625.
Divisibility by 9 and 3
The tests for divisibility by 9, and in turn by 3, arise from the fact that 9 is 1 less than 10.
When 1 or any power of 10 is divided by 9, the remainder is 1. For example,
| 1 ÷ 9 | = 0 remainder 1 | |
| 10 ÷ 9 | = 1 remainder 1 | |
| 100 ÷ 9 | = 11 remainder 1 | |
| 1000 ÷ 9 | = 111 remainder 1 |
Multiplying each by a single digit number less than 9,
| 4 ÷ 9 | = 0 remainder 4 | |
| 50 ÷ 9 | = 5 remainder 5 | |
| 200 ÷ 9 | = 22 remainder 2 | |
| 9000 ÷ 9 | = 999 remainder 9; better written as 1000 remainder 0. |
The remainder when 9254 is divided by 9 is the same as the remainder when
9 + 2 + 5 + 4 = 20 is divided by 9. The general result is
- When a number, and the sum of its digits, are both divided by 9, the remainders are
the same.
Because 9 is a multiple of 3, the remainders after division by 3 follows a similar pattern,
4 and 4 have the same remainder after division by 3.
50 and 5 have the same remainder after division by 3.
200 and 2 have the same remainder after division by 3.
9000 and 9 have the same remainder after division by 3.
Adding these results, 9254 and 9 + 2 + 5 + 4 = 20 have the same remainder when divided by 3. The general result is
- When a number, and the sum of its digits, are both divided 3, the remainders are the same.
For example,
| 167 ÷ 9 = 18 remainder 5 | and | 167 ÷ 3 = 55 remainder 2 | ||
| (1 + 6 + 7) ÷ 9 = 1 remainder 5 | (1 + 6 + 7) ÷ 3 = 4 remainder 2 |
Example
Find the remainders when 62 574 is divided by 9 and by 3.
Solution
The sum of the digits is 6 + 2 + 5 + 7 + 4 = 24, and 2 + 4 = 6.
Hence 62 574 has remainder 6 when divided by 9, and remainder 0 when divided by 3.
With most students in Years 7−8, however, only the corresponding divisibility tests
are appropriate:
- A number is divisible by 9 if the sum of its digits is divisible by 9.
- A number is divisible by 3 if the sum of its digits is divisible by 3.
Example
Test for divisibility by 3 and by 9:
a![]() 71 325 618
71 325 618 ![]() b
b![]() 36 867 924
36 867 924
Solution
- a
- The sum of the digits is 7 + 1 + 3 + 2 + 5 + 6 + 1 + 8 = 33, and 3 + 3 = 6.
Hence 71 325 618 is divisible by 3, but not by 9. - b
- The sum of the digits is 3 + 6 + 8 + 6 + 7 + 9 + 2 + 4 = 45, and 4 + 5 = 9.
Hence 36 867 924 is divisible by 3 and by 9.
Divisibility by 11
The test for divisibility by 11 arises from the fact that 11 is 1 more than 10, but 9 × 11 = 99 is 1 less than 100.
When 1 or any power of 10 is divided by 11, the remainder is alternately 1 and 10, but we shall regard the remainder 10 as being remainder −1.
| 1 ÷ 11 | = 0 remainder 1 | |
| 10 ÷ 11 | = 0 remainder 10; which we will regard as remainder −1 | |
| 100 ÷ 11 | = 9 remainder 1 | |
| 1000 ÷ 11 | = 91 remainder 10; which we will regard as remainder −1 | |
| 10 000 ÷ 11 | = 909 remainder 1 | |
| 100 000 ÷ 11 | = 9091 remainder 10; which we will regard as remainder −1 |
Multiplying each result by a single digit number,
| 4 ÷ 11 | leaves remainder 4 | ||
| 20 ÷ 11 | leaves remainder −5 | ||
| 500 ÷ 11 | leaves remainder 2 | ||
| 3000 ÷ 11 | leaves remainder −9 | ||
| 90 000 ÷ 11 | leaves remainder 3 | ||
| 800 000 ÷ 11 | leaves remainder −8 |
Adding these results, the remainder when 893 524 is divided by 11 is the same as the remainder when 4 − 2 + 5 − 3 + 9 − 8 = 7 is divided by 9. It was important here to write the alternating sum of the digits starting at the right-hand end with the units. The general result is,
- When a number is divided by 11, the remainder is the same as the division by 11 of the alternating sum of the digits, starting at the right-hand end with the digits.
For example,
91 627 ÷ 11 = 8329 remainder 8 and (7 − 2 + 6 − 1 + 9) ÷ 11 = 1 remainder 8.
Example
Find the remainders after division by 11 of:
a![]() 62 578
62 578 ![]() b
b![]() 937 565
937 565
Solution
- a
- The alternating sum of the digits is 8 − 7 + 5 − 2 + 6 = 10. Hence 62 578 has remainder 10 when divided by 11.
- b
- The alternating sum of the digits is 5 − 6 + 5 − 7 + 3 − 9 = −9. Hence 937 565 has remainder 11 − 9 = 2 when divided by 11.
As with 3 and 9, only the corresponding divisibility test is usually appropriate in Years 7−8:
- A number is divisible by 11 if the alternating sum of its digits is divisible by 11.
Example
Test for divisibility by 11:
a![]() 71 325 618
71 325 618 ![]() b
b![]() 71 938 471
71 938 471
Solution
- a
- The alternating sum of the digits is 8 − 1 + 6 − 5 + 2 − 3 + 1 − 7 = 1.
Hence 71 325 618 is not divisible by 11. - b
- The alternating sum of the digits is 1 − 7 + 4 − 8 + 3 − 9 + 1 − 7 = −22.
Hence 71 938 471 is divisible by 11.
Divisibility by numbers that are not prime powers
We can combine the previous tests for divisibility by testing separately for divisibility by the highest power of each prime. Here are examples of some such tests:
- A number is divisible by 6 = 2 × 3 if it is divisible by 2 and by 3.
- A number is divisible by 12 = 4 × 3 if it is divisible by 4 and by 3.
- A number is divisible by 15 = 3 × 5 if it is divisible by 3 and by 5.
- A number is divisible by 18 = 2 × 9 if it is divisible by 2 and by 9.
- A number is divisible by 66 = 2 × 3 × 11 if it is divisible by 2, by 3 and by 11.
Divisibility by powers of 10 is particularly simple—just count the number of zeroes.
Example
- a
- Test 726 for divisibility by 6, 12 and 18.
- b
- Test 6875 for divisibility by 55 and 275.
Solution
- a
- Factoring the three divisors, 6 = 2 × 3, 12 = 4 × 3 and 18 = 2 × 9. By looking at the last digit and the last two digits, 726 is divisible by 2, but not by 4.
The sum of the digits is 15, so 726 is divisible by 3, but not by 9.
Hence 726 is divisible by 6, but not by 12 or 18. - b
- Factoring the two divisors, 55 = 5 × 11 and 275 = 25 × 11. By looking at the last digit and the last two digits, 6875 is divisible by 5 and by 25.
- c
- The alternating sum of the digits is 5 − 7 + 8 − 6 = 0, so 6875 is divisible by 11.
Hence 6875 is divisible by 55 and by 275.
The multiplication table is one of the best-known objects in arithmetic. It is formed by doing nothing more that writing out the first twelve non-zero multiples of each number from 1 to 12 in twelve successive rows. (Or perhaps they were written out in twelve successive columns.)
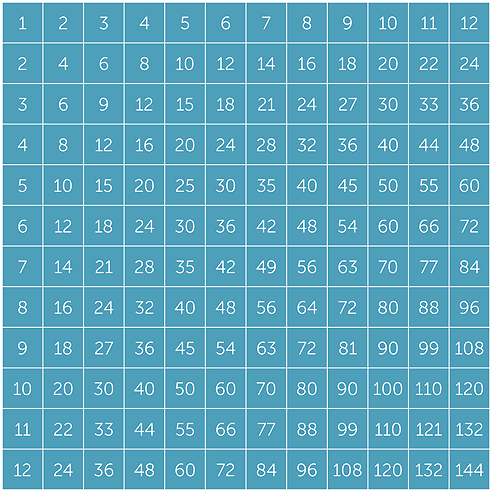
Despite the simplicity of its construction, it is a very powerful object indeed, and well justifies the recommendation to learn it by heart. Here are some of its many properties — students routinely find many more.
- All products from 1 × 1 to 12 × 12 are contained in the table. The answer to 9 × 7 is 63, which is located at the entry in the 7th row and the 9th column (or the 9th row and the 7th column).
- The LCM of any two numbers up to 12 can be found from the table. The LCM of 8 and 10 is 40, which is the first common entry in the 8th and 10th rows (or in the 8th and 10th columns).
- The numbers on the leading diagonal from 1 in the top left to 144 in the bottom right are the squares 1, 4, 9, 16,…
- The whole table is symmetric about the leading diagonal. This illustrates the fact that multiplication is commutative, meaning, for example, that 7 × 9 = 9 × 7.
- What is the pattern formed by shading all the even numbers? Every second column and every second row is shaded, leaving isolated odd numbers. We saw above how all multiples of even numbers are even, and that odd and even numbers alternate in the multiples of an odd number.
- What is the pattern formed by shading all the multiples of 3? This time every third row and every third column is shaded.
Students often see many more patterns in this table. The following exercise gives some less obvious properties, but the proofs are omitted, because they require quite serious algebra. Once sequences and series are being studied, perhaps in Year 11, the table is well worth revisiting because of the insights it can give into sequences and into the use of algebra.
Exercise 19
- a
- What pattern is formed by shading the numbers that are multiples of 4?
- b
- What pattern is formed by the differences between successive terms
on any diagonal parallel to the leading diagonal? - c
- Now take the opposite diagonal passing through the square 49 from top right
to bottom left. What numbers arise when we subtract each from 49?
What happens with parallel diagonals through other squares?
There are five useful laws, collectively called the index laws, that help us manipulate powers. At this stage, they are best established by examples and learnt verbally.
After algebra has been introduced, however, they can be presented in their more
familiar algebraic formulation. For later reference, they are summarised here verbally
and algebraically:
- To multiply powers of the same base, add the indices.
am × an = am + n
- To divide powers of the same base, subtract the indices.
am ÷ an = am − n
- To raise a power to a power, multiply the indices.
(am)n = amn
- The power of a product is the product of the powers.
(ab)n = anbn
- The power of a quotient is the quotient of the powers.
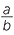 n =
n = 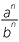
Multiplying powers with the same base
If we write out the powers as continued products, we can quickly see what is happening when we multiply powers with the same base.
![]() 75 × 73 = (7 × 7 × 7 × 7 × 7) × (7 × 7 × 7) = 78
75 × 73 = (7 × 7 × 7 × 7 × 7) × (7 × 7 × 7) = 78
There are 5 + 3 = 8 factors of 7 in the product, so the product is 78.
- To multiply powers with the same base, add the indices. For example,
75 × 73 = 78
Dividing powers with the same base
We can use the same approach with dividing powers with the same base.
![]() 75 ÷ 73 = (7 × 7 × 7 × 7 × ) ÷ (7 × 7 × 7) = 72
75 ÷ 73 = (7 × 7 × 7 × 7 × ) ÷ (7 × 7 × 7) = 72
There are 5 − 3 = 2 factors of 7 in the quotient, so the quotient is 72.
- To divide powers with the same base, subtract the indices. For example,
75 ÷ 73 = 72
EXAMPLE
Simplify each expression, leaving the answer as a power.
a![]() 32 × 35
32 × 35 ![]() b
b![]() 57 ÷ 53
57 ÷ 53 ![]() c
c![]() 109 ÷ 103
109 ÷ 103 ![]() d
d![]() 129 × 125 ÷ 122
129 × 125 ÷ 122
Solution
a![]() 32 × 35 = 37
32 × 35 = 37 ![]() b
b![]() 57 ÷ 53 = 54
57 ÷ 53 = 54 ![]() c
c![]() 109 ÷ 103 = 106
109 ÷ 103 = 106 ![]() d
d![]() 129 × 125 ÷ 122 = 1212
129 × 125 ÷ 122 = 1212
The examples above have carefully avoided questions like 73 ÷ 75, where the divisor is a higher power than the dividend. Such questions are better written as fractions,
![]()
 =
= 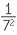
![]() or
or![]()
 = 7-2
= 7-2
The first form can be covered once fractions have been introduced. The second form requires negative indices, which are usually regarded as a little too sophisticated for Years 7−8.
Raising a power to a power
We often need to deal with expressions such as (73)4 in which a power is raised to a power. Writing out just the outer power allows us to apply the previous law.
| |
(73)4 | = 73 × 73 × 73 × 73 |
| |
= 712 |
There are 3 × 4 factors of 7 in the expression, so it simplifies to 712.
- To raise a power to a power, multiply the indices. For example,
![]() (73)4 = 712
(73)4 = 712
EXAMPLE
Simplify each expression, leaving the answer as a power:
a![]() (65)7
(65)7 ![]() b
b![]() (103)5
(103)5 ![]() c
c![]() (42)3 × (43)2
(42)3 × (43)2![]() d
d![]() (115)4 ÷ (116)3
(115)4 ÷ (116)3
Solution
|
a |
(65)7 = 635 |
b |
(103)5 = 1015 |
|||
|
c |
(42)3 × (43)2 = 46 × 46 = 412 |
d |
(115)4 ÷ (116)3 = 1120 ÷ 1118 = 112 |
The power of a product
The fourth law deals with a power of a product. Again, we can write out the power.
| (2 × 3)4 | = (2 × 3) × (2 × 3) × (2 × 3) × (2 × 3) | |
| = (2 × 2 × 2 × 2) × (3 × 3 × 3 × 3) | ||
| = 24 × 34 |
These steps rely heavily on the any-order property of multiplication to regroup the
4 factors of 2 and the 4 factors of 3.
- The power of a product is the product of the powers. For example,
![]() (2 × 3)4 = 24 × 34
(2 × 3)4 = 24 × 34
Example
Write each expression without brackets, leaving the answer in index notation.
a (3 × 7)4 ![]() b (8 × 12)6
b (8 × 12)6 ![]() c (3 × 5)4 × (3 × 7)3
c (3 × 5)4 × (3 × 7)3![]() d (5 × 7 × 9)6 ÷ (55)2
d (5 × 7 × 9)6 ÷ (55)2
Solution
| a | (3 × 7)4 = 34 × 74 | b | (8 × 12)6 = 86 × 126 | |||||
| c | (3 × 5)4 × (3 × 7)3 | = 34 × 54 × 33 × 73 | d | (5 × 7 × 9)16 ÷ (55)2 | = 516 × 716 × 916 ÷ 510 | |||
| = 37 × 54 × 73 | = 56 × 716 × 916 | |||||||
The power of a quotient
The final index law deals with the power of a quotient. It is clumsy to formulate this law using the division sign, so fraction notation for division is used for the only time in this module.
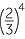 |
= 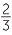 × × 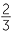 × × 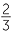 × × 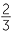 |
|
= 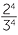 |
The same process can be done with the power of any fraction, giving the general result,
- The power of a quotient is the quotient of the powers. For example,
![]()
 =
= 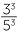
EXAMPLE
Simplify each expression, evaluating the resulting powers:
a ![]()

![]() b
b![]()
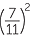
![]() c
c![]()
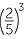
![]() d
d![]()
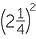
Solution
|
a |
|
b |
|
|||
|
c |
|
d |
|
The index laws and mental arithmetic
‘A power of a product is the product of powers’ is useful in mental arithmetic, both forwards and in reverse. For example,
| 204 | = (2 × 10)4 | 32 × 125 | = 25 × 53 | |||
| = 24 × 104 | = 22 × (2 × 5)3 | |||||
| = 16 × 10 000 | and | = 22 × 103 | ||||
| = 160 000 | = 4 × 1000 | |||||
| = 4000 |
Because our system of numerals has base 10, isolating powers of 10 is always good practice. In the first example, we factored 20 as 20 = 2 × 10. In the second example, we combined factors of 2 and factors of 5 to make factors of 10.
Exercise 20
Show how to calculate these expressions using the index laws to work with powers of 10.
a![]() 30004
30004 ![]() b
b![]() 4 000 0003
4 000 0003 ![]() c
c![]() 625 × 8000
625 × 8000![]() d
d![]() 40003 × 503
40003 × 503
The HCF and LCM are essential for the study of fractions, which are introduced in the module Fractions. To express a fraction in simplest form, we cancel the HCF of the numerator and denominator, and to add and subtract fractions, we usually use the LCM of their denominators as a common denominator,
![]()
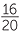 =
= 
![]() and
and ![]()
 +
+  =
= 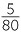 +
+ 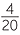 =
= 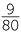 .
.
The HCF of two algebraic expressions is important in factoring. The first step in the systematic factoring of an expression is to take out the HCF of the terms:
![]() 3ax2 − 6a2x = 3ax(x − 2a).
3ax2 − 6a2x = 3ax(x − 2a).
Factoring by taking out the HCF is first considered in the module Algebraic Expressions, and developed further in the module, Negatives and the Index Laws.
Prime numbers are the building blocks of all whole numbers when we take them apart by factoring. For example, we can write 60 as a product of primes,
![]() 60 = 22 × 3 × 5.
60 = 22 × 3 × 5.
Every composite number has one and only one prime factorisation. Prime factorisation is the central concern of the module Primes and Prime Factorisation. This module also shows how prime factorisation yields more systematic approaches to the calculations of the HCF and LCM.
The five index laws have been introduced in the present module in the context of whole numbers, although it was mentioned that the fifth law, and a clearer statement of the second law, require fractions. The modules, Negatives and the Index Laws and Special Expansions and Algebraic Fractions extend them to rational numbers and also give them an algebraic formulation, although the indices are still only nonzero whole numbers. The later module The Index Laws extends the indices to any rational number.
The presentation in this module has been carried out arithmetically, and entirely within the whole numbers. There have been no algebra or fractions except in the occasional remark and exercise that looks forward to later content. Arrays, rather than areas, have been used to represent products, so that the whole-number aspect of the ideas can be emphasised. It is important in later years, when algebra has been used to generalise the content, not to lose the arithmetic intuition of the present module.
All the present material was expounded by the ancient Greek mathematicians. The idea of representing numbers by arrays was developed particularly by Pythagoras and his school, who developed theories about what we now call ‘figurate numbers’. These include the triangular numbers discussed in this module, and pentagonal and tetrahedral numbers.
Exercise 2
Here is ‘odd minus odd equals even’. The other cases are similar.
 −
−  =
= 
Exercise 3
- a
- The quotient of an even number and an even number may be even or odd.
For example, 12 ÷ 6 = 2 and 12 ÷ 4 = 3. - b
- The quotient of an even number and an odd number is always even.
For example, 12 ÷ 3 = 4. - c
- (When an odd number is divided by an even number, the remainder is never zero.)
- d
- The quotient of an odd number and an odd number is always odd. For example,
35 ÷ 5 = 7.
Exercise 4
For addition,
| 2a + 2b | = 2(a + b) | |
| (2a + 1) + 2b | = 2(a + b) + 1 | |
| (2a + 1) + (2b + 1) | = 2(a + b + 1) |
For multiplication,
| (2a) × (2b) | = 2 × 2ab | |
| (2a) × (2b + 1) | = 2 × a(2b + 1) | |
| (2a + 1) × (2b + 1) | = 4ab + 2a + 2b + 1 | |
| = 2(2ab + a + b) + 1 |
Exercise 5
- a
- All the numbers have a trivial array.
The number 1 and the primes 2, 3, 5, 7 and 11 each have only a trivial array.
The composite numbers 4, 6, 8, 9 and 12 each have at least one other array.
The even numbers 2, 4, 6, 8, 10 and 12 are those with a 2-row array.
The squares 4 and 9 also have a square array.
The numbers 6 and 10 each have only one non-trivial rectangular array.
The number 8 has the three-dimensional array and a 2 × 4 array.
The number 12 has three two-dimensional arrays because 12 = 1 × 12 = 2 × 6 = 3 × 4, and also has a three-dimensional 2 × 2 × 3 array. - b
- The 15 primes less than 50 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
The number 2 is the only even prime number. - c
- There are five two-dimensional arrays 36 = 1 × 36 = 2 × 18 = 3 × 12 = 4 × 9 = 6 × 6.
There are three three-dimensional arrays 36 = 2 × 2 × 9 = 2 × 3 × 6 = 3 × 3 × 4. - d
- There are four arrays 16 = 1 × 16 = 2 × 8 = 4 × 4 = 2 × 2 × 4. If we had four dimensions at our disposal, we could draw the array corresponding to 16 = 2 × 2 × 2 × 2.
- e
- Various responses
- f
- The smallest number greater than 1 that is both square and cubic is 64 = 8 × 8 = 4 × 4 × 4.
If we had use of six dimensions, we could draw the array 64 = 2 × 2 × 2 × 2 × 2 × 2. - g
- There are a great many ways to arrange 30 objects in a rectangular pattern or three dimensional block with no wasted space. The numbers 29 and 31 are prime, so except for packing all the items in a row, any packing into a block will have empty spaces.
Exercise 6
- a
- The dots in the lower left triangle of the square array are the reflection of the dots in the upper right triangle.
- b
- It follows immediately from part a that the difference is even. Alternatively, the square of an even number is even and the square of an odd number is odd, and the difference of two even numbers or two odd numbers is even.
Exercise 7
- a
- If each side of the square has, for example 7 dots, then the total numbers of dots is
6 + 6 + 6 + 6 = 4 × 6. - b
- Take the larger of the two arrays, and keep removing its outer layer until it becomes the smaller array. At each step, the side length of the array goes down by 2, and the number of dots removed is a multiple of 4.
Exercise 8
- a
- The difference increases by 1 each time, because each new row has one more dot.
- b
- 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210,…
- c
- Two odds, then two evens, then two odds, then two evens,…
Every time an odd number is added, the sum changes from even to odd or from odd to even. When an even number is added, however, the sum either stays even or stays odd.
Exercise 9
The diagram shows that the 4th triangular number is (4 × 5) ÷ 2 = 10.
Similarly, the 100th triangular number is (100 × 101) ÷ 2 = 5050.
Exercise 10
- a
- All the numbers except for the last number in the row have the same quotient. For example, the entries in the 5th row have quotient 4 when divided by 7.
- b
- All the numbers in, for example, the 5th column have remainder 5 when divided by 7.
Exercise 11
The remainders when 22 and 41 are divided by 6 are 4 and 5, whose sum is 9.
But 9 = 6 + 3, so the remainder when dividing 63 by 6 is 3.
Exercise 12
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
The factors of 160 are 1, 2, 4, 5, 8, 10, 16, 20, 32 40, 80, 160.
Exercise 13
- a
- The numbers 12 and 20 have HCF 4 and LCM 60, and 4 × 60 = 12 × 20.
- b
- When 12 and 20 are divided by their HCF, which is 4, the resulting numbers are
3 and 5, and the numbers 3 and 5 have HCF 1. - c
- When the LCM, which is 60, is divided by 12 and by 20, the resulting numbers are
5 and 3, and the numbers 5 and 3 have HCF 1.
(Notice that the resulting numbers in parts b and c are the same.)
Exercise 14
- a
- 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225,…
- b
- 0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728,…
Exercise 15
- a
- 25 = 52 + 02 = 32 + 42.
- b
- 50 = 52 + 52 = 72 + 12.
- c
- 65 = 82 + 12 = 72 + 42.
- d
- 1729 = 123 + 13 = 103 + 93.
Exercise 16
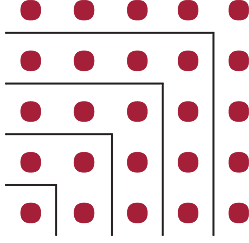
Exercise 18
201 = 128 + 64 + 8 + 1 = 27 + 26 + 23 + 1, so in base 2 notation, 201 = 11 001 001.
Exercise 19
- a
- Every fourth row and every fourth column is shaded, together with the numbers in the exact centre of the remaining squares.
- b
- The differences along each diagonal parallel to the leading diagonal increase by 2
each time. - c
- The differences from 49 are:
12 when 1 step away, 22 when 2 steps away, 32 when 3 steps away,…
The same pattern of differences occurs along each parallel diagonal through a square, for example,
4 × 6 = 52 − 12, 3 × 7 = 52 − 22, 2 × 8 = 52 − 32, 1 × 9 = 52 − 42
Exercise 20
| a | 30004 | = 34 × (103)4 | |
| = 81 × 1012 | |||
| = 81 000 000 000 000 |
| b | 4 000 0003 | = 43 × (106)3 | |
| = 64 × 1018 | |||
| = 64 000 000 000 000 000 000 |
| c | 625 × 8000 | = 54 × 23 × 103 | |
| = 5 × 103 × 103 | |||
| = 5 000 000 |
| d | 40003 × 503 | = (4000 × 50)3 |
|
| = 200 0003 |
|||
| = 8 000 000 000 000 000 |
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()