The Improving Mathematics Education in Schools (TIMES) Project
- Fluency with addition, subtraction, multiplication and division of whole
numbers including: - understanding that subtraction is the inverse operation to addition
(The statement 32 + 54 = 86 is equivalent to the statement 86 − 54 = 32.)
- understanding that division is the inverse operation of multiplication (division without remainder)
(The statement 6 × 4 = 24 is equivalent to the statement 24 ÷ 4 = 6.)
- the use of the commutative, associative and distributive laws in calculations
(For example: 23 + 34 + 17 + 36 = (23 + 17) + (34 + 36) = 40 + 70 = 110 and
37 × 6 = (30 + 7) × 6 = 30 × 6 + 7 × 6 = 180 + 42 = 222)
- the role of 0 and 1
- division with remainder
- The highest common factor (HCF) and lowest common multiple (LCM) of two whole numbers.
- Using a number line for whole numbers, including:
- order
- addition and subtraction
- multiplication as repeated addition
- division with and without remainder
- Using arrays and areas as models for multiplication.
- Some experience with shading simple fractions of areas.
Traditionally, the term ‘fraction’ was used to describe a part of a whole. The word comes from the Latin frango − I break. In this module, we will take a fraction to mean a non-negative rational number, that is, a number of the form 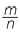 , where n is a positive integer and m is a positive integer or 0. (See Links Forward for further discussion on the definition of a fraction)
, where n is a positive integer and m is a positive integer or 0. (See Links Forward for further discussion on the definition of a fraction)
Fractions arise naturally in everyday situations involving sharing, cutting up and proportions. For example, the bathtub was one-third full, three quarters of the class walk to school. Fractions between 0 and 1 describe parts of a whole. Fractions extend the whole numbers to a number system in which division by a non-zero number always makes sense. While decimals can be used to represent fractions, many numbers are simpler in fraction notation. For example, 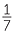 compared to 0.142857....
compared to 0.142857....
Some computations are much easier if we use fractions rather than decimals.
For example, the fraction 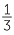 has decimal equivalent 0.33333... but it is much easier
has decimal equivalent 0.33333... but it is much easier
to find 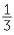 × 12 than to try to find 0.333... × 12.
× 12 than to try to find 0.333... × 12.
In this module we will only be concerned with positive fractions and zero.
For the fraction 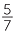 , the top number is called the numerator, the line is called
, the top number is called the numerator, the line is called
the vinculum and the bottom number is called the denominator.
Proper fractions and improper fractions
We call a fraction a proper fraction if the numerator is smaller than the denominator.
For example, 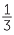 and
and 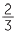 are proper fractions (A proper fraction x lies in the interval
are proper fractions (A proper fraction x lies in the interval
0 ≤ x < 1 and if a fraction lies in this interval it is proper.)
If the numerator is greater than or equal to the denominator, the fraction is said to be an improper fraction. Examples of improper fractions include 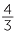 and
and 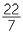 . (An improper fraction x lies in the interval x ≥ 1 and any fraction ≥ 1 is improper.)
. (An improper fraction x lies in the interval x ≥ 1 and any fraction ≥ 1 is improper.)
If the numerator and denominator are equal, then the fraction is equal to 1, so 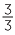 = 1.
= 1.
Whole numbers can be expressed as fractions, for example, 4 = 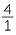 and some fractions are equal to a whole number, for example
and some fractions are equal to a whole number, for example 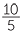 = 2. Indeed, every whole number can be written as a fraction in infinitely many different ways.
= 2. Indeed, every whole number can be written as a fraction in infinitely many different ways.
For example: 1 = 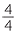 , 2 =
, 2 = 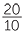 =
= 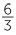 , 3 =
, 3 = 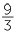 =
= 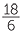 .
.
There are two main ways to represent fractions.
- As markers on a number line.
- Shading parts of a square, called an area diagram.
The number line
The number line has already been used to represent whole numbers.
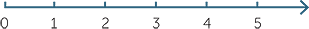
To represent, for example, fractions with denominator 3, we divide each unit
segment into three equal segments and label the markers as shown.
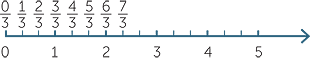
From 0, the marker for 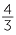 is reached by taking four steps to the right each of length
is reached by taking four steps to the right each of length 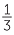 .
.
Area diagrams
We can also represent fractions by shading areas.
The squares below are each considered to have area 1.
The shaded part represents a fraction of the whole.
The shaded areas below represent the fractions 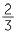 and
and 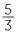 .
.

Each of the two models has its advantages.
The number line is better to use for addition, subtraction and order.
The area model is better to explain multiplication of fractions.
- We say that two fractions are equivalent if they mark the same point on the
number line.
For example, if we mark 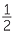 and
and 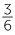 on a number line, then we mark the same point.
on a number line, then we mark the same point.
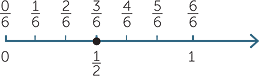
That is, 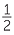 and
and 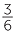 are equivalent fractions.
are equivalent fractions.
- Starting with a fraction, the fractions obtained by multiplying its numerator
and denominator by the same whole number are equivalent.
For example: 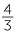 =
= 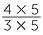 =
= 
- Starting with a fraction, the fractions obtained by dividing its numerator and denominator by the same whole number are equivalent.
For example:  =
= 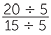 =
= 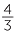
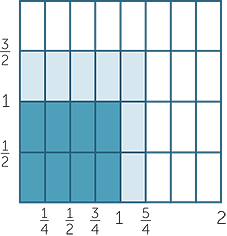
A fraction is said to be in simplest form if the only common factor of the numerator and the denominator is 1. To reduce a fraction to an equivalent fraction in simplest form we use the method of cancelling. For example, when reducing 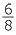 to its simplest form we divide the top (numerator) and bottom (denominator) by the highest common factor of 6 and 8, which is 2.
to its simplest form we divide the top (numerator) and bottom (denominator) by the highest common factor of 6 and 8, which is 2.
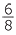 =
= 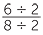 =
= 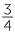
We can use cancelling notation to write this process efficiently.
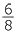 =
= 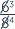 =
= 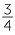
For some fractions it is more convenient to cancel in stages.
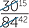 =
= 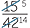 =
= 
Exercise 1
a Use a number line to illustrate 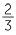 =
= 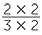 =
= 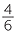 and
and 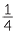 =
= 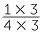 =
= 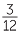
b Complete the set of equivalent fractions: 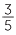 =
=  =
=  =
= 
If I had 4 friends over for dinner and ordered three family sized pizzas, how much would each of us get if I shared it equally between the 5 of us? If three pizzas are shared equally among five people, then each one receives 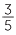 of a pizza.
of a pizza.
Division of a whole number by another non-zero whole number always gives a fraction.
If we have 7 pizzas to be shared among 5 friends, then each would receive 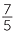 pizzas.
pizzas.
But this is clearly the same as 1 pizza each, plus 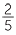 of a pizza. Thus the improper fraction
of a pizza. Thus the improper fraction 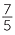 is the same as 1
is the same as 1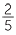 .
.
When a line segment of length equal to 4 is divided into 3 equal segments, each segment has length 4 ÷ 3 = 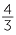 .
.

Dividing the whole number m by the whole number n, that is, m ÷ n results in the fraction 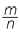 . On the number line, the line segment from 0 to m is divided into n equal parts, each part has length
. On the number line, the line segment from 0 to m is divided into n equal parts, each part has length 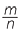 .
.
For example, 7 ÷ 3 = 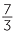
![]() and
and![]() 2 ÷ 7 =
2 ÷ 7 = 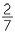
A mixed numeral consists of a whole number plus a fraction, for example 3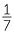 = 3 +
= 3 + 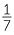 .
.
Every improper fraction can be written as a mixed numeral and vice versa.
For example, 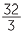 = 32 ÷ 3 = 10
= 32 ÷ 3 = 10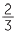 .
.
In order to write 10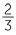 as an improper fraction, we write:
as an improper fraction, we write:
10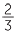 |
= 10 + 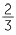 |
|
= 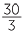 + + 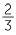 |
||
= 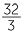 |
Exercise 2
There are approximately 365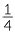 days in a year. Express this mixed numeral as an improper fraction.
days in a year. Express this mixed numeral as an improper fraction.
If two fractions have the same denominator then it is easy to decide which is the larger. It is the one with the larger numerator.
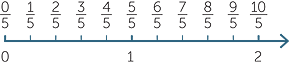
One number is greater than another if it lies to the right of that number on the number line.
Hence we can see from the number line that 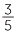 >
> 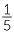 , and
, and 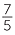 >
> 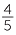 .
.
Using common denominators
If the denominators of two fractions are not equal, it is more difficult to see which of the two fractions is larger. In this case, we can use equivalent fractions.
To compare 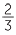 and
and 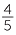 , first find a common denominator. The lowest common denominator is the lowest common multiple of the two denominators, which in this example is 15.
, first find a common denominator. The lowest common denominator is the lowest common multiple of the two denominators, which in this example is 15.
Now 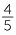 =
=  and
and 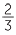 =
=  and so
and so 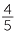 is larger than
is larger than 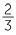 .
.
Exercise 3
a Find a fraction which lies between 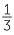 and
and 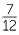 . What about
. What about 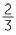 and
and 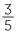 ?
?
b List the fractions  ,
, 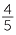 ,
,  and
and 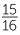 from smallest to largest.
from smallest to largest.
Addition of fractions is straightforward if the denominators are the same. To find 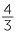 +
+ 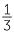 ,
,
you take a step to the right of 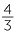 from 0 followed by a step to the right of
from 0 followed by a step to the right of 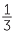 to arrive at
to arrive at 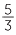 .
.
Of course this is exactly the same process as with the whole numbers and the number line.

Thus, when the denominators of the fractions to be added are the same,
we add the numerators.
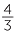 +
+ 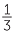 =
= 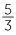
When the denominators are different, we use equivalent fractions to express
the fractions using a common denominator and then proceed exactly as before:
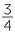 + + 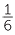 |
= 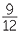 + + 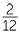 |
= 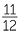 |
We can add mixed numerals together simply by adding together the whole number parts and then adding the fractions.
Here is an example of how to deal with this:
3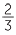 + 4 + 4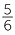 |
= 7 + 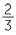 + + 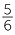 |
|
= 7 + 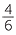 + + 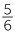 |
||
= 7 + 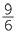 |
||
= 7 + 1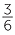 |
||
= 8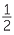 |
Note that the commutative and associative laws for addition have been used in obtaining the result.
Exercise 4
a Find two different fractions that add to give 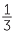 .
.
b What mixed number when added to 3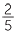 + 4
+ 4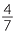 makes 10?
makes 10?
Subtracting fractions uses similar ideas to addition of fractions. If the denominators
of the two fractions are equal, subtraction is straightforward.
To find 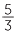 −
− 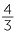 , move
, move 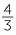 units to the left, starting from
units to the left, starting from 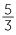 . Thus
. Thus 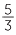 −
− 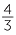 =
= 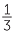 .
.

When the denominators of the fractions to be subtracted are the same,
we subtract the second numerator from the first.
If the denominators are not equal, we use equivalent fractions to find
a common denominator.
Thus, to find 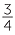 −
− 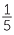 , we convert to equivalent fractions with denominator 20.
, we convert to equivalent fractions with denominator 20.
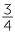 −
− 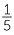 =
= 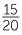 −
−  =
= 
We can subtract mixed numerals in a variety of ways. Here are two methods.
Method 1 |
Method 2 |
|||
| Convert to improper fractions | Deal with whole numbers | |||
4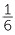 − 2 − 2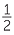 |
=  − − 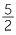 |
4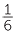 − 2 − 2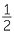 |
= 3 − 2 + 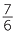 − − 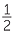 |
|
=  − − 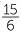 |
= 1 + 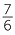 − − 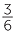 |
|||
= 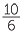 |
= 1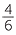 |
|||
= 1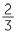 |
= 1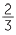 |
|||
When the whole number ‘parts’ of the mixed numerals are large then
For example:
258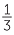 − 254 − 254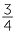 |
= 257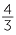 − 254 − 254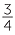 |
= 257 − 254 +  − − 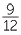 |
|
= 3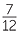 |
Exercise 5
What fraction when added to 4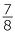 gives 6
gives 6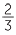 ?
?
Multiplication of fractions and ‘of’
In mathematics, when we are asked, for example, to find 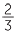 of 18 oranges,
of 18 oranges,
we take it to mean that we divide the 18 oranges into three equal parts and
then take two of these parts.

This gives 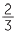 of 18 = 12.
of 18 = 12.
Note that the result is the same as 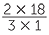 =
= 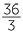 = 12.
= 12.
Using a number line with ‘of’
This method can be extended. For example, to find 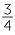 of
of 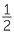 :
:
we first calculate 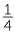 of
of 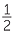 and then multiply by 3.
and then multiply by 3.
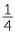 of
of 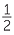 can be illustrated by using a number line, by first dividing the interval 0 to
can be illustrated by using a number line, by first dividing the interval 0 to 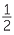 into 4 equal parts.
into 4 equal parts.
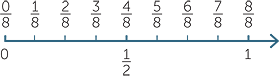
| We can see that | 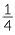 of of 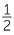 is is  |
| and | 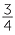 of of 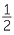 is is 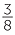 . . |
Using the area model for multiplication
A diagram to explain how to multiply 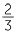 ×
× 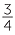 is shown below. The base is divided into three equal intervals (denominators of the first fraction). The height is divided into 4 equal intervals (denominators of the second fraction). The square, which has area 1, is divided into 3 × 4 = 12 (the denominators are multiplied together) rectangles of equal area. Each of the rectangles has area equal to
is shown below. The base is divided into three equal intervals (denominators of the first fraction). The height is divided into 4 equal intervals (denominators of the second fraction). The square, which has area 1, is divided into 3 × 4 = 12 (the denominators are multiplied together) rectangles of equal area. Each of the rectangles has area equal to 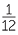 .
.
The rectangle with side lengths 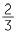 and
and 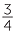 is shaded.
is shaded.
Notice that 2 × 3 = 6 is the number of shaded boxes (the numerators are multiplied together).
 |
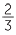 × × 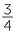 = = 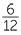 = = 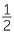 |
You get the same shaded region if you first shade 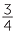 of the square and then shade
of the square and then shade 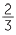 of the shaded section. This shows that
of the shaded section. This shows that 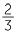 of
of 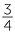 gives the same result as
gives the same result as 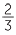 ×
× 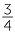 through the area model. Of course,
through the area model. Of course, 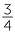 of
of 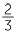 also gives the same result as
also gives the same result as 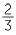 ×
× 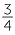 through the area model.
through the area model.
Here is a diagram which can be used to illustrate 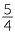 ×
× 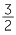 =
= 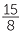 = 1
= 1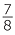 .
.
 |
The dark blue square shows a unit square. It is divided into 8 equal parts. |
In summary:
- To multiply two fractions together, multiply the two numerators together
and the two denominators together and simplify if possible:
For example, 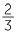 ×
× 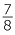 =
= 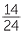 =
= 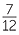
- Multiplication of two fractions and the corresponding ‘of’ statement
give the same answer.
Exercise 6
Use an area diagram to illustrate each of the multiplications.
a 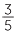 ×
× 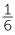
![]() b
b ![]() 1
1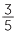 × 1
× 1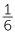
Let us find 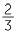 ×
× 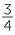 .
.
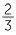 ×
× 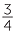 =
= 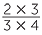 =
= 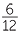 =
= 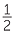
We cancelled down the second last fraction to its lowest form, after doing the multiplication.
There is a shorthand way of writing this, which often simplifies the process of multiplication.
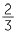 ×
× 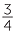 =
= 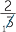 ×
× 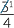 =
= 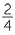 =
= 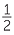
This process is called cancelling. The cancellation can take place because you are doing the same operation to both numerator and denominator which we know gives an equivalent fraction.
Exercise 7
What is the total length of 6 pieces of ribbon if each piece is 8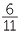 cm?
cm?
When multiplying two mixed numerals, we can convert both into improper fractions before multiplying. For example,
3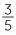 × 4
× 4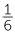 =
= 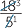 ×
× 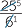 =
= 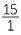 = 15
= 15
Dividing a whole number by a whole number
We have considered dividing a whole number by a whole number in a previous section of this module. It was found that dividing a whole number by a whole number gives a fraction. For example,
4 ÷ 3 = 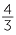 and 17 ÷ 5 =
and 17 ÷ 5 = 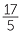 = 3
= 3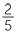
The division statement 4 ÷ 3 = 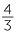 , has an equivalent multiplication statement to 3 ×
, has an equivalent multiplication statement to 3 × 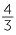 = 4.
= 4.
Also note that dividing by 3 gives the same result as multiplying by 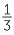 .
.
In general, for whole numbers m and n, dividing m by n is the same as multiplying m by 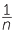 . Note that
. Note that 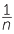 is called the reciprocal of n.
is called the reciprocal of n.
Division of a fraction by a whole number
The idea of performing a division by multiplying by the reciprocal can also be used to divide a fraction by a whole number. For example, 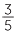 ÷ 6 means that we take the fraction
÷ 6 means that we take the fraction 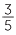 and divide it into 6 equal parts.
and divide it into 6 equal parts.
This can be illustrated by drawing a unit square divided into fifths. Shade 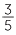 (shown in
(shown in
blue below) and further divide the square into 6 equal horizontal strips.
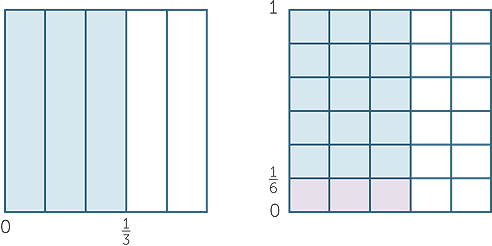
The purple shaded area  represents
represents 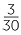 =
=  .
.
It can be seen that to divide 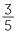 by 6 , we multiply
by 6 , we multiply  by the reciprocal of 6.
by the reciprocal of 6.
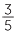 ÷ 6 =
÷ 6 = 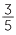 ×
× 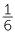 =
= 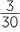 =
= 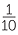
In general, when a fraction 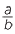 is divided by a whole number n, the result is
is divided by a whole number n, the result is
the same as when 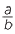 is multiplied by the reciprocal of n,
is multiplied by the reciprocal of n, 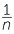 .
.
Exercise 8
Use a number line to consider each division and give an interpretation of each division in terms of ‘how many’.
a 1 ÷ 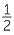 , 3 ÷
, 3 ÷ 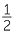 , 1 ÷
, 1 ÷ 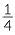 , 3 ÷
, 3 ÷ 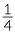
b 1 ÷ 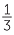 , 1 ÷
, 1 ÷ 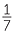 , 3 ÷
, 3 ÷ 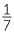
Dividing a fraction by a fraction
We will look at this in two ways. First we will repeat the division of the previous section.
Approach 1 (common denominator) The division 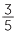 ÷ 6 can be written as
÷ 6 can be written as 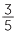 ÷
÷ 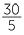 .
.
The division is now expressed in fifths. That is, 3 fifths divided by 30 fifths = 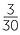 =
= 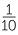 .
.
Approach 2 (a little algebra) 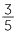 ÷ 6 is the number x that when multiplied by 6 gives
÷ 6 is the number x that when multiplied by 6 gives 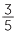 .
.
6x = 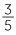 . Multiply both sides by 5, 5 × 6x = 3, 30x = 3. Therefore x =
. Multiply both sides by 5, 5 × 6x = 3, 30x = 3. Therefore x = 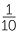 .
.
A new question:  ÷
÷ 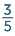 = ?
= ?
Approach 1 (common denominator) The division 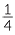 ÷
÷ 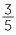 can be written as
can be written as 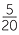 ÷
÷ 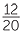 .
.
The division is now expressed in twentieths.
That is, 5 twentieths divided by 12 twentieths = 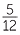 .
.
Approach 2 (a little algebra) 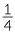 ÷
÷ 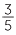 is the number x that when multiplied by
is the number x that when multiplied by 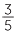 gives
gives 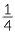 .
.
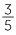 x =
x = 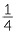 . Multiply both sides by 4, 4 ×
. Multiply both sides by 4, 4 × 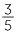 x = 1, 12x = 5. Therefore x =
x = 1, 12x = 5. Therefore x = 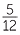 .
.
Division and reciprocals (Approach 3)
The reciprocal of a fraction is the fraction obtained by swapping the numerator
and denominator.
Hence the reciprocal of 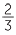 is
is 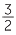 . Dividing by
. Dividing by 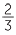 is the same as multiplying by its reciprocal
is the same as multiplying by its reciprocal 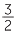 .
.
Thus, 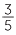 ÷
÷ 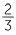 =
= 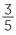 ×
× 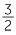 =
= 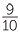 .
.
In general, when a fraction 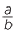 is divided by a fraction
is divided by a fraction 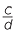 , the result is the same as when
, the result is the same as when 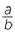 is multipled by the reciprocal of
is multipled by the reciprocal of 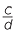 , that is multiplied by
, that is multiplied by 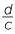 .
.
For example, 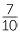 ÷
÷ 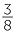 =
= 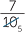 ×
× 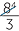 =
= 
Note that, 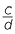 ×
× 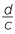 =
= 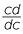 = 1.
= 1.
As with multiplication, to divide two mixed numerals we convert both to improper fractions.
3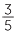 ÷ 4
÷ 4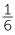 =
=  ÷
÷ 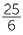 =
=  ×
× 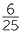 =
= 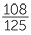
exercise 9
A plumber has a piece of pipe which is 7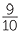 metres in length and has to cut it into 5 equal pieces. How long must each piece be?
metres in length and has to cut it into 5 equal pieces. How long must each piece be?
An understanding of fractions is crucial before meeting decimals.
The techniques and ideas that are used in the four operations on fractions are needed when numbers are replaced with pronumerals. Hence algebraic competence and progress in school mathematics relies heavily on fluency with fractional arithmetic.
Many algebraic formulas used in both mathematics and science involve fractions.
For example, the volume of a sphere V = 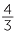 πr3 and Ohm’s law I =
πr3 and Ohm’s law I = 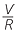 , involve fractions.
, involve fractions.
All fractions have either terminating or recurring decimal expansions and conversely every number that has a terminating or recurring decimal representation is a fraction.
Probability calculations rely heavily on fractions, as do problems involving percentages, rates and ratios.
In this module a fraction is a positive rational number - negative rational numbers are also fractions. The term fraction is used in a number of ways. A surd like 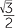 is sometimes referred to as a fraction, as is an algebraic expression such as
is sometimes referred to as a fraction, as is an algebraic expression such as 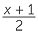 . Techniques similar to those developed in this module can be applied to surds and algebraic expressions.
. Techniques similar to those developed in this module can be applied to surds and algebraic expressions.
A formal construction of the rational numbers is given in the module, The Real Numbers. Negative fractions are discussed in the module, Fractions and the Index Laws in Algebra.
In general, the ancient civilisations avoided fractions by giving special names to parts of various measures. We still do this today. For example, instead of saying 1 hours we say
hours we say
1 hour 13 minutes.
Egyptian fraction notation was developed in the Middle Kingdom of Egypt (2080−1640 BC), altering the Old Kingdom’s Eye of Horus numeration system.
With few exceptions they wrote all their fractions as unit fractions, that is, with numerator 1. To write the unit fractions used in their Egyptian fraction notation the Egyptians placed the hieroglyph  above the numeral for the denominator.
above the numeral for the denominator.
For example 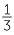 =
= 
There were separate symbols for some common non-unit fractions such as 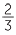 and
and 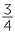
but most fractions, as we know them, were expressed as a sum of unit fractions.
For example 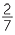 can be written as
can be written as 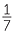 +
+ 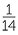 +
+ 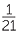 +
+ 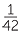 .
.
Note that if p is an odd number, then 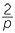 =
= 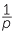 +
+ 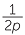 +
+ 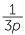 +
+ 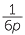 gives a formula for expressing fractions of this form as a sum of unit fractions.
gives a formula for expressing fractions of this form as a sum of unit fractions.
Exercise 10
a Prove the identity 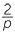 =
= 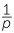 +
+ 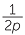 +
+ 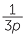 +
+ 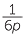 where p is a non-zero whole number and use it to write
where p is a non-zero whole number and use it to write 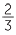 as the sum of four different unit fractions.
as the sum of four different unit fractions.
b Prove the identity 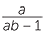 =
=  +
+ 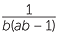 and use it to split
and use it to split  into unit fractions.
into unit fractions.
The Rhind papyrus (1650 BC) and other ancient sources have been used to explore the methods the Egyptians used in calculating with Egyptian fractions.
While the Egyptians used fractions as objects − we do not know exactly what they thought of them. Up until the Hellenistic period the Greeks preferred to think of fractions in terms of ratios and proportions. They did not tend to think of them as we do, and certainly not as points on the number line.
Hindu mathematicians are believed to be the first to indicate fractions with numbers rather than words. Brahmagupta (c. 628) and Bhaskara (c. 1150) were early Hindu mathematicians who wrote fractions as we do today, but without the bar (vinculum). They wrote one number above the other to indicate a fraction.
The next step in the evolution of fraction notation was the addition of the horizontal fraction bar. This is generally credited to the Arabs who used the Hindu notation, then improved on it by inserting this bar in between the numerator and denominator, which was later named the vinculum. Later on, Fibonacci (c.1175-1250), was the first European mathematician to use the vinculum as it is used today.
EXERCISE 1
a For 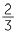 =
= 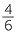 , draw an interval from 0 to 1. Mark
, draw an interval from 0 to 1. Mark 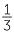 and
and 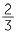 on it. Divide each of the three subintervals formed into two equal parts. The interval from 0 to 1 is now divided into subintervals of length one sixth.
on it. Divide each of the three subintervals formed into two equal parts. The interval from 0 to 1 is now divided into subintervals of length one sixth.
For 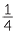 =
= 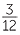 , draw an interval from 0 to 1. Mark
, draw an interval from 0 to 1. Mark 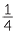 ,
, 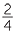 and
and 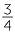 on it. Divide each of the four subintervals into 3 equal parts. The interval from 0 to 1 is now divided into subintervals of length one twelfth.
on it. Divide each of the four subintervals into 3 equal parts. The interval from 0 to 1 is now divided into subintervals of length one twelfth.
b 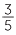 =
=  =
= 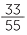 =
= 
EXERCISE 2
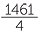
EXERCISE 3
a 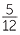 - infinitely many possible answers
- infinitely many possible answers
 - infinitely many possible answers
- infinitely many possible answers
b 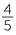 ,
, 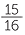 ,
,  ,
, 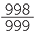
EXERCISE 4
a 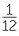 +
+ 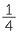 =
= 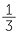 or
or 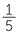 +
+  =
= 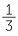
b 2
EXERCISE 5
1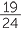
EXERCISE 6
a One unit square divided into five equal columns and 6 equal rows to form 30 rectangles of equal area. Shade 3× 1 = 3 rectangles.
b A square 2 units by 2 units consisting of 4 unit squares. Divide each unit square into five equal columns and six equal rows. Shade 8 × 7 = 56 rectangles.
EXERCISE 7
51 cm
cm
EXERCISE 8
- a
- How many halves in 1? (Number line with 0, 1 and one half marked)
How many halves in 3? (Number line with 0, 1, 2 and 3 and the halves marked)
How many quarters in 1? (Number line with 0, 1 and the quaters marked)
How many quarters in 3? (Number line with 0,1, 2 and 3 and the quarters marked) - b
- How many thirds in 1?
How many sevenths in 1?
How many sevenths in 3?
EXERCISE 9
1 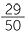 m or 1.58 m
m or 1.58 m
EXERCISE 10
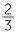 =
= 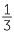 +
+ 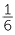 +
+  +
+ 
 =
=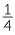 +
+ 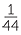
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


