The Improving Mathematics Education in Schools (TIMES) Project
- Addition and subtraction of whole numbers.
- Familiarity with the English words
‘and’, ‘or’, ‘not’, ‘all’, ‘if…then’.
In all sorts of situations we classify objects into sets of similar objects and count them. This procedure is the most basic motivation for learning the whole numbers and learning how to add and subtract them.
Such counting quickly throws up situations that may at first seem contradictory.
‘Last June, there were 15 windy days and 20 rainy days, yet 5 days were neither windy nor rainy.’
How can this be, when June only has 30 days? A Venn diagram, and the language of sets, easily sorts this out.
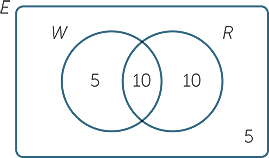 Let W be the set of windy days,
Let W be the set of windy days,
and R be the set of rainy days.
Let E be the set of days in June.
Then W and R; together have size 25, so
the overlap between W and R is 10.; The Venn diagram opposite displays; the whole situation.
The purpose of this module is to introduce language for talking about sets, and some notation for setting out calculations, so that counting problems such as this can be sorted out. The Venn diagram makes the situation easy to visualise.
A set is just a collection of objects, but we need some new words and symbols and diagrams to be able to talk sensibly about sets.
In our ordinary language, we try to make sense of the world we live in by classifying collections of things. English has many words for such collections. For example, we speak of ‘a flock of birds’, ‘a herd of cattle’, ‘a swarm of bees’ and ‘a colony of ants’.
We do a similar thing in mathematics, and classify numbers, geometrical figures and other things into collections that we call sets. The objects in these sets are called the elements of the set.
Describing a set
A set can be described by listing all of its elements. For example,
![]() S = { 1, 3, 5, 7, 9 },
S = { 1, 3, 5, 7, 9 },
which we read as ‘S is the set whose elements are 1, 3, 5, 7 and 9’. The five elements of the set are separated by commas, and the list is enclosed between curly brackets.
A set can also be described by writing a description of its elements between curly brackets. Thus the set S above can also be written as
![]() S = { odd whole numbers less than 10 },
S = { odd whole numbers less than 10 },
which we read as ‘S is the set of odd whole numbers less than 10’.
A set must be well defined. This means that our description of the elements of a set is clear and unambiguous. For example, { tall people } is not a set, because people tend to disagree about what ‘tall’ means. An example of a well-defined set is
![]() T = { letters in the English alphabet }.
T = { letters in the English alphabet }.
Equal sets
Two sets are called equal if they have exactly the same elements. Thus following the usual convention that ‘y’ is not a vowel,
![]() { vowels in the English alphabet } = { a, e, i, o, u }
{ vowels in the English alphabet } = { a, e, i, o, u }
On the other hand, the sets { 1, 3, 5 } and { 1, 2, 3 } are not equal, because they have different elements. This is written as
![]() { 1, 3, 5 } ≠ { 1, 2, 3 }.
{ 1, 3, 5 } ≠ { 1, 2, 3 }.
The order in which the elements are written between the curly brackets does not matter at all. For example,
![]() { 1, 3, 5, 7, 9 } = { 3, 9, 7, 5, 1 } = { 5, 9, 1, 3, 7 }.
{ 1, 3, 5, 7, 9 } = { 3, 9, 7, 5, 1 } = { 5, 9, 1, 3, 7 }.
If an element is listed more than once, it is only counted once. For example,
![]() { a, a, b } = { a, b }.
{ a, a, b } = { a, b }.
The set { a, a, b } has only the two elements a and b. The second mention of a is an unnecessary repetition and can be ignored. It is normally considered poor notation to list an element more than once.
The symbols ∈ and ∉
The phrases ‘is an element of’ and ‘is not an element of’ occur so often in discussing sets that the special symbols ∈ and ∉ are used for them. For example, if A = { 3, 4, 5, 6 }, then
![]() 3 ∈ A (Read this as ‘3 is an element of the set A’.)
3 ∈ A (Read this as ‘3 is an element of the set A’.)
![]() 8 ∉ A (Read this as ‘8 is not an element of the set A’.)
8 ∉ A (Read this as ‘8 is not an element of the set A’.)
Describing and naming sets
- A set is a collection of objects, called the elements of the set.
- A set must be well defined, meaning that its elements can be described and
listed without ambiguity. For example:
{ 1, 3, 5 } and { letters of the English alphabet }.
- Two sets are called equal if they have exactly the same elements.
- The order is irrelevant.
- Any repetition of an element is ignored.
- If a is an element of a set S, we write a ∈ S.
- If b is not an element of a set S, we write b ∉ S.
EXERCISE 1
- a
- Specify the set A by listing its elements, where
A = { whole numbers less than 100 divisible by 16 }. - b
- Specify the set B by giving a written description of its elements, where
B = { 0, 1, 4, 9, 16, 25 }. - c
- Does the following sentence specify a set?
C = { whole numbers close to 50 }.
Finite and infinite sets
All the sets we have seen so far have been finite sets, meaning that we can list all their elements. Here are two more examples:
![]() { whole numbers between 2000 and 2005 } = { 2001, 2002, 2003, 2004 }
{ whole numbers between 2000 and 2005 } = { 2001, 2002, 2003, 2004 }
![]() { whole numbers between 2000 and 3000 } = { 2001, 2002, 2003,…, 2999 }
{ whole numbers between 2000 and 3000 } = { 2001, 2002, 2003,…, 2999 }
The three dots ‘…’ in the second example stand for the other 995 numbers in the set. We could have listed them all, but to save space we have used dots instead. This notation can only be used if it is completely clear what it means, as in this situation.
A set can also be infinite − all that matters is that it is well defined. Here are two examples of infinite sets:
![]() { even whole numbers } = { 0, 2, 4, 6, 8, 10, …}
{ even whole numbers } = { 0, 2, 4, 6, 8, 10, …}
![]() { whole numbers greater than 2000 } = { 2001, 2002, 2003, 2004, …}
{ whole numbers greater than 2000 } = { 2001, 2002, 2003, 2004, …}
Both these sets are infinite because no matter how many elements we list, there are always more elements in the set that are not on our list. This time the dots ‘…’ have a slightly different meaning, because they stand for infinitely many elements that we could not possibly list, no matter how long we tried.
The numbers of elements of a set
If S is a finite set, the symbol | S | stands for the number of elements of S. For example:
![]() If S = { 1, 3, 5, 7, 9 }, then | S | = 5.
If S = { 1, 3, 5, 7, 9 }, then | S | = 5.
![]() If A = { 1001, 1002, 1003, …, 3000 }, then | A | = 2000.
If A = { 1001, 1002, 1003, …, 3000 }, then | A | = 2000.
![]() If T = { letters in the English alphabet }, then | T | = 26.
If T = { letters in the English alphabet }, then | T | = 26.
The set S = { 5 } is a one-element set because | S | = 1. It is important to distinguish between the number 5 and the set S = { 5 }:
![]() 5 ∈ S but 5 ≠ S .
5 ∈ S but 5 ≠ S .
The empty set
The symbol ∅ represents the empty set, which is the set that has no elements at all. Nothing in the whole universe is an element of ∅:
![]() | ∅ | = 0 and x ∉ ∅, no matter what x may be.
| ∅ | = 0 and x ∉ ∅, no matter what x may be.
There is only one empty set, because any two empty sets have exactly the same elements, so they must be equal to one another.
Finite and Infinite sets
- A set is called finite if we can list all of its elements.
- An infinite set has the property that no matter how many elements we list,
there are always more elements in the set that are not on our list. - If S is a finite set, the symbol | S | stands for the number of elements of S.
- The set with no elements is called the empty set, and is written as ∅.
Thus | ∅ | = 0. - A one-element set is a set such as S = { 5 } with | S | = 1.
EXERCISE 2
- a
- Use dots to help list each set, and state whether it is finite or infinite.
- i
- B = { even numbers between 10 000 and 20 000 }
- ii
- A = { whole numbers that are multiples of 3 }
- b
- If the set S in each part is finite, write down | S |.
- i
- S = { primes }
- ii
- S = { even primes }
- iii
- S = { even primes greater than 5 }
- iv
- S = { whole numbers less than 100 }
- c
- Let F be the set of fractions in simplest form between 0 and 1 that can be written with a single-digit denominator. Find F and | F |.
Subsets of a set
Sets of things are often further subdivided. For example, owls are a particular type of bird, so every owl is also a bird. We express this in the language of sets by saying that the set of owls is a subset of the set of birds.
A set S is called a subset of another set T if every element of S is an element of T. This is written as
![]() S ⊆ T (Read this as ‘S is a subset of T’.)
S ⊆ T (Read this as ‘S is a subset of T’.)
The new symbol ⊆ means ‘is a subset of’. Thus { owls } ⊆ { birds } because every owl is a bird. Similarly,
![]() if A = { 2, 4, 6 } and B = { 0, 1, 2, 3, 4, 5, 6 }, then A ⊆ B,
if A = { 2, 4, 6 } and B = { 0, 1, 2, 3, 4, 5, 6 }, then A ⊆ B,
because every element of A is an element of B.
The sentence ‘S is not a subset of T’ is written as
![]() S
S ![]() T.
T.
This means that at least one element of S is not an element of T. For example,
{ birds } ![]() { flying creatures }
{ flying creatures }
because an ostrich is a bird, but it does not fly. Similarly,
![]() if A = { 0, 1, 2, 3, 4 } and B = { 2, 3, 4, 5, 6 }, then A
if A = { 0, 1, 2, 3, 4 } and B = { 2, 3, 4, 5, 6 }, then A ![]() B,
B,
because 0 ∈ A, but 0 ∉ B.
The set itself and the empty set are always subsets
Any set S is a subset of itself, because every element of S is an element of S. For example:
![]() { birds } ⊆ { birds } and { 1, 2, 3, 4, 5, 6 } = { 1, 2, 3, 4, 5, 6 }.
{ birds } ⊆ { birds } and { 1, 2, 3, 4, 5, 6 } = { 1, 2, 3, 4, 5, 6 }.
Furthermore, the empty set ∅ is a subset of every set S, because every element of the empty set is an element of S, there being no elements in ∅ at all. For example:
![]() ∅ ⊆ { birds } and ∅ ⊆ { 1, 2, 3, 4, 5, 6 }.
∅ ⊆ { birds } and ∅ ⊆ { 1, 2, 3, 4, 5, 6 }.
Every element of the empty set is a bird, and every element of the empty set is one of the numbers 1, 2, 3, 4, 5 or 6.
Subsets and the words ‘all’ and ‘if … then’
A statement about subsets can be rewritten as a sentence using the word ‘all’.
For example,
|
{ owls } ⊆ { birds } |
|
means |
|
‘All owls are birds.’ |
|
{ multiples of 4 } ⊆ { even numbers } |
means |
‘All multiples of 4 are even.’ |
||
|
{ rectangles } ⊆ { rhombuses } |
means |
‘Not all rectangles are rhombuses.’ |
They can also be rewritten using the words ‘if … then’. For example,
| { owls } ⊆ { birds } | means | ‘If a creature is an owl, then it is a bird.’ | ||
| { multiples of 4 } ⊆ { even numbers } | means | ‘If a number is a multiple of 4, then it is even’: | ||
| { rectangles } ⊆ { rhombuses } | means | ‘If a figure is a rectangle, then it may not be a square.’ | ||
Venn diagrams
Diagrams make mathematics easier because they help us to see the whole situation at a glance. The English mathematician John Venn (1834−1923) began using diagrams to represent sets. His diagrams are now called Venn diagrams.
In most problems involving sets, it is convenient to choose a larger set that contains all of the elements in all of the sets being considered. This larger set is called the universal set, and is usually given the symbol E. In a Venn diagram, the universal set is generally drawn as a large rectangle, and then other sets are represented by circles within this rectangle.

For example, if V = { vowels }, we could choose the universal set as E = { letters of the alphabet } and all the letters of the alphabet would then need to be placed somewhere within the rectangle, as shown below.
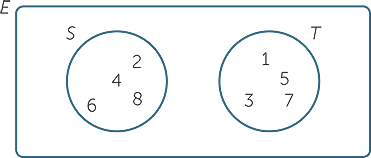
In the Venn diagram below, the universal set is E = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }, and each of these numbers has been placed somewhere within the rectangle.
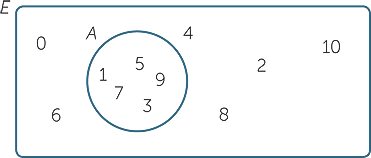
The region inside the circle represents the set A of odd whole numbers between 0 and 10. Thus we place the numbers 1, 3, 5, 7 and 9 inside the circle, because A = { 1, 3, 5, 7, 9 }. Outside the circle we place the other numbers 0, 2, 4, 6, 8 and 10 that are in E but not in A.
Representing subsets on a Venn diagram
When we know that S is a subset of T, we place the circle representing S inside the circle representing T. For example, let S = { 0, 1, 2 }, and T = { 0, 1, 2, 3, 4 }. Then S is a subset of T, as illustrated in the Venn diagram below.
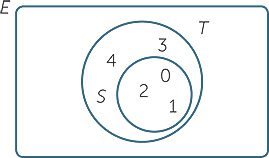
Make sure that 5, 6, 7, 8, 9 and 10 are placed outside both circles>
Subsets and the number line
The whole numbers are the numbers 0, 1, 2, 3,… These are often called the ‘counting numbers’, because they are the numbers we use when counting things. In particular, we have been using these numbers to count the number of elements of finite sets. The number zero is the number of elements of the empty set.
The set of all whole numbers can be represented by dots on the number line.

Any finite subset of set of whole numbers can be represented on the number line. For example, here is the set { 0, 1, 4 }.
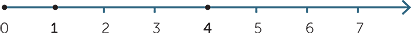
Subsets of a st
- If all the elements of a set S are elements of another set T, then S is called a subset of T. This is written as S ⊆ T.
- If at least one element of S is not an element of T, then S is not a subset of T. This is written as S
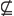 T.
T. - If S is any set, then ∅ ⊆ S and S ⊆ S.
- A statement about a subset can be rewritten using the words ‘all’ or ‘if … then’.
- Subsets can be represented using a Venn diagram.
- The set { 0, 1, 2, 3, 4, … } of whole numbers is infinite.
- The set of whole numbers, and any finite subset of them, can be represented on the number line.
EXERCISE 3
- a
- Rewrite in set notation:
- i
- All squares are rectangles.
- ii
- Not all rectangles are rhombuses.
- b
- Rewrite in an English sentence using the words ‘all’ or ‘not all’:
- i
- { whole number multiples of 6 } ⊆ { even whole numbers }.
- ii
- { square whole numbers } ⊆ { even whole numbers }.
- c
- Rewrite the statements in part (b) in an English sentence using the words ‘if …, then’.
- d
- Given the sets A = { 0, 1, 4, 5 } and B = { 1, 4 }:
- i
- Draw a Venn diagram of A and B using the universal set U = { 0, 1, 2, … , 8 }.
- ii
- Graph A on the number line.
Complements, intersections and unions
The complement of a set
Suppose that a suitable universal set E has been chosen. The complement of a set S
is the set of all elements of E that are not in S. The complement of S is written as Sc.
For example,
![]() If E = { letters } and V = { vowels }, then Vc = { consonants }
If E = { letters } and V = { vowels }, then Vc = { consonants }
![]() If E = { whole numbers } and O = { odd whole numbers },
If E = { whole numbers } and O = { odd whole numbers },
![]() then Oc = {even whole numbers}.
then Oc = {even whole numbers}.
Complement and the word ‘not’
The word ‘not’ corresponds to the complement of a set. For example, in the two examples above,
![]() Vc = { letters that are not vowels } = { consonants }
Vc = { letters that are not vowels } = { consonants }
![]() Oc = { whole numbers that are not odd } = { even whole numbers }
Oc = { whole numbers that are not odd } = { even whole numbers }
The set Vc in the first example can be represented on a Venn diagram as follows.

The intersection of two sets
The intersection of two sets A and B consists of all elements belonging to A and to B.
This is written as A ∩ B. For example, some musicians are singers and some play an instrument.
| |
If |
A = { singers } and B = { instrumentalists }, then |
|
|
A ∩ B = { singers who play an instrument }. |
Here is an example using letters.
| |
If |
V = { vowels } and F = { letters in ‘dingo’ }, then |
|
|
V ∪ F = { i, o }. |
This last example can be represented on a Venn diagram as follows.
Intersection and the word ‘and’
The word ‘and’ tells us that there is an intersection of two sets. For example:
![]() { singers } ∩ { instrumentalists } = { people who sing and play an instrument }
{ singers } ∩ { instrumentalists } = { people who sing and play an instrument }
![]() { vowels } ∩ { letters of ‘dingo’ } = { letters that are vowels and are in ‘dingo’ }
{ vowels } ∩ { letters of ‘dingo’ } = { letters that are vowels and are in ‘dingo’ }
The union of two sets
The union of two sets A and B consists of all elements belonging to A or to B. This is written as A ∪ B. Elements belonging to both set belong to the union. Continuing with the example of singers and instrumentalists:
![]() If A = { singers } and B = { instrumentalists }, then A ∪ B = { musical performers }.
If A = { singers } and B = { instrumentalists }, then A ∪ B = { musical performers }.
In the case of the sets of letters:
![]() If V = { vowels } and F = { letters in ‘dingo’ }, then V &acup; F = { a, e, i, o, u, d, n, g }.
If V = { vowels } and F = { letters in ‘dingo’ }, then V &acup; F = { a, e, i, o, u, d, n, g }.
Union and the word ‘or’
The word ‘or’ tells us that there is a union of two sets. For example:
![]() { singers } ∪ { instrumentalists } = { people who sing or play an instrument }
{ singers } ∪ { instrumentalists } = { people who sing or play an instrument }
![]() { vowels } ∪ { letters in ‘dingo’ } = { letters that are vowels or are in ‘dingo’ }
{ vowels } ∪ { letters in ‘dingo’ } = { letters that are vowels or are in ‘dingo’ }
The word ‘or’ in mathematics always means ‘and/or’, so there is no need to add ‘or both’ to these descriptions of the unions. For example,
| |
If |
A = { 0, 2, 4, 6, 8, 10, 12, 14 } and B = { 0, 3, 6, 9, 12 }, then |
|
|
A ∪ B = { 0, 2, 3, 4, 6, 8, 9, 10, 12, 14 }. |
Here the elements 6 and 12 are in both sets A and B.
Disjoint sets
Two sets are called disjoint if they have no elements in common. For example:
![]() The sets S = { 2, 4, 6, 8 } and T = { 1, 3, 5, 7 } are disjoint.
The sets S = { 2, 4, 6, 8 } and T = { 1, 3, 5, 7 } are disjoint.

Another way to define disjoint sets is to say that their intersection is the empty set,
![]() Two sets A and B are disjoint if A ∩ B = ∅.
Two sets A and B are disjoint if A ∩ B = ∅.
In the example above,
![]() S ∩ T = ∅ because no number lies in both sets.
S ∩ T = ∅ because no number lies in both sets.
Complement, intersection and union
Let A and B be subsets of a suitable universal set E.
- The complement Ac is the set of all elements of E that are not in A.
- The intersection A ∩ B is the set of all elements belonging to A and to B.
- The union A ∪ B is the set of all elements belonging to A or to B.
- In mathematics, the word ‘or’ always means ‘and/or’, so all the elements that
are in both sets are in the union. - The sets A and B are called disjoint if they have no elements in common, that is,
if A ∩ B = ∅.
Representing the complement on a Venn diagram
Let A = { 1, 3, 5, 7, 9 } be the set of odd whole numbers less than 10, and take the universal set as E = { 0, 1, 2, … , 10 }. Here is the Venn diagram of the situation.
The region inside the circle represents the set A, so we place the numbers 1, 3, 5, 7 and 9 inside the circle. Outside the circle, we place the other numbers 0, 2, 4, 6, 8 and 10 that are not in A. Thus the region outside the circle represents the complement Ac = {0, 2, 4, 6, 8, 10}.
Representing the intersection and union on a Venn diagram
The Venn diagram below shows the two sets
![]() A = { 1, 3, 5, 7, 9 } and B = { 1, 2, 3, 4, 5 }.
A = { 1, 3, 5, 7, 9 } and B = { 1, 2, 3, 4, 5 }.
- The numbers 1, 3 and 5 lie in both sets, so we place them in the overlapping region of the two circles.
- The remaining numbers in A are 7 and 9. These are placed inside A, but outside B.
- The remaining numbers in B are 2 and 4. These are placed inside B, but outside A.
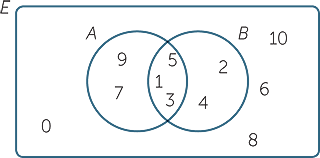
Thus the overlapping region represents the intersection A ∩ B = { 1, 3, 5 }, and the two circles together represent the union A ∪ B = { 1, 2, 3, 4, 5, 7, 9 }.
The four remaining numbers 0, 6, 8 and 10 are placed outside both circles.
Representing disjoint sets on a Venn diagram
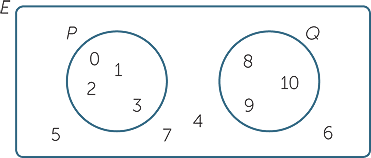
When we know that two sets are disjoint, we represent them by circles that do not intersect. For example, let
![]() P = { 0, 1, 2, 3 }
P = { 0, 1, 2, 3 } ![]() and
and ![]() Q = { 8, 9, 10 }
Q = { 8, 9, 10 }
Then P and Q are disjoint, as illustrated in the Venn diagram below.
Venn diagrams with complements, unions and intersections
- Sets are represented in a Venn diagram by circles drawn inside a rectangle representing the universal set.
- The region outside the circle represents the complement of the set.
- The overlapping region of two circles represents the intersection of the two sets.
- Two circles together represent the union of the two sets.
- When two sets are disjoint, we can draw the two circles without any overlap.
- When one set is a subset of another, we can draw its circle inside the circle of the other set.
EXERCISE 4
Let the universal set be E = {whole numbers less than 20 }, and let
![]() A = { squares less than 20 }
A = { squares less than 20 }
![]() B = { even numbers less than 20 }
B = { even numbers less than 20 }
![]() C = { odd squares less than 20 }
C = { odd squares less than 20 }
- a
- Draw A and C on a Venn diagram, and place the numbers in the correct regions.
- b
- Draw B and C on a Venn diagram, and place the numbers in the correct regions.
- c
- Shade A ∩ B on a Venn diagram, and place the numbers in the correct regions.
- d
- Shade A ∪ B on a Venn diagram, and place the numbers in the correct regions.
Solving problems using a Venn diagram
Keeping count of elements of sets
Before solving problems with Venn diagrams, we need to work out how to keep count of the elements of overlapping sets.
 The upper diagram to the right shows two
The upper diagram to the right shows two
sets A and B inside a universal set E, where
![]() | A | = 6
| A | = 6 ![]() and
and![]() | B | = 7,
| B | = 7,
with 3 elements in the intersection A ∩ B.
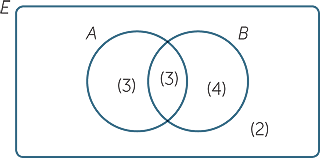 The lower diagram to the right shows only the
The lower diagram to the right shows only the
number of elements in each of the four regions.
These numbers are placed inside round brackets
so that they don’t look like elements.
You can see from the diagrams that
| A | = 6 and | B | = 7, but | A ∪ B | ≠ 6 + 7.
The reason for this is that the elements inside the overlapping region A ∩ B should only be counted once, not twice. When we subtract the three elements of A ∩ B from the total, the calculation is then correct.
| A ∪ B | = 6 + 7 − 3 = 10.
EXAMPLE
 In the diagram to the right,
In the diagram to the right,
| A | = 15, | B | = 25, | A ∩ B | = 5 and | E | = 50.
- a
- Insert the number of elements into each
of the four regions. - b
- Hence find | A ∪ B | and | A ∩ Bc |
Solution
- a
- We begin at the intersection and work outwards.
The intersection A ∩ B has 5 elements.
Hence the region of A outside A ∩ B has 10 elements,
and the region of B outside A ∩ B has 20 elements.
This makes 35 elements so far, so the outer region has 15 elements. - b
- From the diagram, | A ∪ B | = 35 and | A ∩ Bc | = 10.
EXERCISE 5
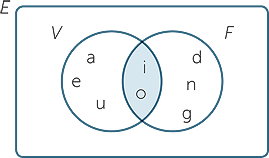
- a
- Draw a Venn diagram of two sets S and T
- b
- Given that | S | = 15, | T | = 20, | S ∪ T | = 25 and | E | = 50, insert the number of elements into each of the four regions.
- c
- Hence find | S ∩ T | and | S ∩ Tc |.
Number of elements in the regions of a Venn diagram
| • | The numbers of elements in the regions of a Venn diagram can be done by working systematically around the diagram. |
||
| • | The number of elements in the union of two sets A and B is | ||
| • | Number of elements in A ∪ B = number of elements in A | ||
| • | Number of elements in A ∪ B | = number of elements in A |
|
| + number of elements in B | |||
| − number of elements in A ∩ B. | |||
| • | Writing this formula in symbols, | A ∪ B | = | A | + | B | − | A ∩ B |. | ||
Solving problems by drawing a Venn diagram
Many counting problems can be solved by identifying the sets involved, then drawing up a Venn diagram to keep track of the numbers in the different regions of the diagram.
EXAMPLE
A travel agent surveyed 100 people to find out how many of them had visited the cities of
Melbourne and Brisbane. Thirty-one people had visited Melbourne, 26 people had been to Brisbane, and 12 people had visited both cities. Draw a Venn diagram to find the number of people who had visited:
a![]() Melbourne or Brisbane
Melbourne or Brisbane
b![]() Brisbane but not Melbourne
Brisbane but not Melbourne
c![]() only one of the two cities
only one of the two cities
d![]() neither city.
neither city.
Solution
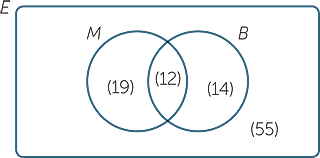 Let M be the set of people who had
Let M be the set of people who had
visited Melbourne, and let B be the set
of people who had visited Brisbane.
Let the universal set E be the set of
people surveyed.
The information given in the question can now be rewritten as
![]() | M | = 31,
| M | = 31, ![]() | B | = 26,
| B | = 26, ![]() | M ∩ B | = 12
| M ∩ B | = 12 ![]() and
and![]() | E | = 100.
| E | = 100.
| Hence number in M only | = 31 − 12 |
| = 19 | |
| and number in B only | = 26 − 12 |
| = 14. |
a![]() Number visiting Melbourne or Brisbane = 19 + 14 +12 = 45.
Number visiting Melbourne or Brisbane = 19 + 14 +12 = 45.
b![]() Number visiting Brisbane only = 14.
Number visiting Brisbane only = 14.
c![]() Number visiting only one city = 19 + 14 = 33.
Number visiting only one city = 19 + 14 = 33.
d![]() Number visiting neither city = 100 − 45 = 55.
Number visiting neither city = 100 − 45 = 55.
Problem solving using Venn diagrams
- First identify the sets involved.
- Then construct a Venn diagram to keep track of the numbers in the different regions of the diagram.
EXERCISE 6
Twenty-four people go on holidays. If 15 go swimming, 12 go fishing, and 6 do neither, how many go swimming and fishing? Draw a Venn diagram and fill in the number of people in all four regions.
EXERCISE 7
In a certain school, there are 180 pupils in Year 7. One hundred and ten pupils study French, 88 study German and 65 study Indonesian. Forty pupils study both French and German, 38 study German and German only. Find the number of pupils who study:
a |
all three languages |
b |
Indonesian only |
|||
c |
none of the languages |
d |
at least one language |
|||
e |
either one ot two of the three languages. |
|||||
The examples in this module have shown how useful sets and Venn diagrams are in counting problems. Such problems will continue to present themselves throughout secondary school.
The language of sets is also useful for understanding the relationships between objects of different types. For example, we have met various sorts of numbers, and we can summarise some of our knowledge very concisely by writing
![]() { whole numbers } ⊆ { integers } ⊆ { rational numbers } ⊆ { real numbers }.
{ whole numbers } ⊆ { integers } ⊆ { rational numbers } ⊆ { real numbers }.
The relationships amongst types of special quadrilaterals is more complicated. Here are some statements about them.
![]() { squares } ⊆ { rectangles } ⊆ { parallelograms } ⊆ { trapezia }
{ squares } ⊆ { rectangles } ⊆ { parallelograms } ⊆ { trapezia }
![]() { rectangles } ∩ { rhombuses } = { squares }
{ rectangles } ∩ { rhombuses } = { squares }
![]() If A = { convex kites } and B = { non-convex kites }, then
If A = { convex kites } and B = { non-convex kites }, then
![]() A ∩ B = ∅ and A ∪ B = { kites }
A ∩ B = ∅ and A ∪ B = { kites }
That is, the set of convex kites and the set of non-convex kites are disjoint, but their union is the set of all kites.
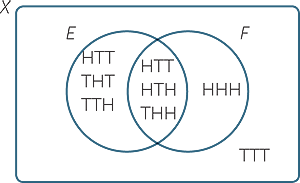
It is far easier to talk about probability using the language of sets. The set of all outcomes is called the sample space, a subset of the sample space is called an event. Thus when we throw three coins, we can take the sample space as the set
![]() S = { HHH, HHT, HTH, HTT, THH, THT, TTH, TTT }
S = { HHH, HHT, HTH, HTT, THH, THT, TTH, TTT }
and the event ‘throwing at least one head and at least one tail’ is then the subset
![]() E = { HHT, HTH, HTT, THH, THT, TTH }
E = { HHT, HTH, HTT, THH, THT, TTH }
Since each outcome is equally likely,
![]() P(at least one head and at least one tail) =
P(at least one head and at least one tail) =  =
=  .
.
The event space of the complementary event ‘throwing all heads or all tails’ is the complement of the event space in the sample space, which we take as the universal set, so
![]() Ec = { HHH, TTT }.
Ec = { HHH, TTT }.
Since | E | + | Ec | = | S |, it follows after dividing by | S | that P(Ec) = 1 − P(E), so
![]() P(throwing all head or all tails) = 1 −
P(throwing all head or all tails) = 1 −  =
=  .
.
Let F be the event ‘throwing at least two heads’. Then
![]() F = { HHH, HHT, HTH, THH }
F = { HHH, HHT, HTH, THH }
A Venn diagram is the best way to sort out the relationship between the two events E and F. We can then conclude that
![]() P(E and F) = 3
P(E and F) = 3 ![]() and
and![]() P(E or F) = 7
P(E or F) = 7
Sets and Functions
When we discuss a function, we usually want to write down its domain − the set of all x-values that we can substitute into it, and its range − the set of all y-values that result from such substitutions.
For example, for the function y = x2,
![]() domain = { real numbers }
domain = { real numbers } ![]() and
and![]() range = {y: y ≥ 0}.
range = {y: y ≥ 0}.
The notation used here for the range is ‘set-builder notation’, which is no longer taught in school. Consequently we mostly avoid set notation altogether, and use instead less rigorous language,
![]() ‘The domain is all real numbers, and the range is y > 0.’
‘The domain is all real numbers, and the range is y > 0.’
Speaking about the condition rather than about the set, however, can confuse some students, and it is often useful to demonstrate the set theory ideas lying behind the abbreviated notation.
Sets and equations
Here are two inequalities involving absolute value and their solution.
|
| x | ≤ 5 (distance from x to 0) ≤ 5 |
| x | ≥ 5 (distance from x to 0) ≥ 5 |
|
|
|
|
|
|
x ≥ −5 and x ≤ 5. |
x ≤ −5 and x ≥ 5. |
If we use the language of solution sets, and pay attention to ‘and’ and ‘or’, we see that the solution of the first inequality is the intersection of two sets, and the solution of the second inequality is the union of two sets. In set-builder notation, the solutions to the two inequalities are
![]() { x: x ≥ −5 } ∩ { x: x ≤ 5 } = { x: −5 ≤ x ≤ 5}, and
{ x: x ≥ −5 } ∩ { x: x ≤ 5 } = { x: −5 ≤ x ≤ 5}, and
![]() { x: x ≤ −5 } ∩ { x: x ≥ 5 } = { x: x £ −5 or x ≥ 5}.
{ x: x ≤ −5 } ∩ { x: x ≥ 5 } = { x: x £ −5 or x ≥ 5}.
At school, however, we simply write the solutions to the two inequalities as the conditions alone,
![]() −5 ≤ x ≤ 5
−5 ≤ x ≤ 5![]() and
and![]() x ≤ −5 or x ≥ 5
x ≤ −5 or x ≥ 5
There are many similar situations where the more precise language of sets may
help to clarify the solutions of equations and inequalities when difficulties are raised during discussions.
Counting problems go back to ancient times. Questions about ‘infinity’ were also keenly discussed by mathematicians in the ancient world. The idea of developing a ‘theory of sets’, however, only began with publications of the German mathematician Georg Cantor in the 1870s, who was encouraged in his work by Karl Weierstrass and Richard Dedekind, two of the greatest mathematicians of all time.
Cantor’s work involved the astonishing insight that there are infinitely many different types of infinity. In the hierarchy of infinities that he discovered, the infinity of the whole numbers is the smallest type of infinity, and is the same as the infinity of the integers and of the rational numbers. He was able to prove, quite simply, that the infinity of the real numbers is very much larger, and that the infinity of functions is much larger again. His work caused a sensation and some Catholic theologians criticised his work as jeopardising ‘God’s exclusive claim to supreme infinity’.
Cantor’s results about types of infinity are spectacular and not particularly difficult. The topic is quite suitable as extension work at school, and the basic ideas have been presented in some details in Appendix 2 of the Module The Real Numbers.
Cantor’s original version of set theory is now regarded as ‘naive set theory’, and contains contradictions. The most famous of these contradictions is called ‘Russell’s paradox’, after the British philosopher and mathematician Bertrand Russell. It is a version of the ancient barber-paradox,
‘A barber shaves all those who do not shave themselves. Who shaves the barber?’
and it works like this:
‘Sets that are members of themselves are rather unwelcome objects.
In order to distinguish such tricky sets from the ordinary, well-behaved sets,
let S be the set of all sets that are not members of themselves.
But when we consider the set S itself, we have a problem.
If S is a member of S, then S is not a member of S.
If S is not a member of S, then S is a member of S.
This is a contradiction.’
The best-known response, but by no means the only response, to this problem and to the other difficulties of ‘naive set theory’ is an alternative, extremely sophisticated, formulation of set theory called ‘Zermelo-Fraenkel set theory’, but it is hardly the perfect solution. While no contradictions have been found,many disturbing theorems have been proven. Most famously, Kurt Goedel proved in 1931 that it is impossible to prove that Zermelo-Fraenkel set theory, and indeed any system of axioms within which the whole numbers can be constructed, does not contain a contradiction!
Nevertheless, set theory is now taken as the absolute rock-bottom foundation of mathematics, and every other mathematical idea is defined in terms of set theory. Thus despite the paradoxes of set theory, all concepts in geometry, arithmetic, algebra and calculus − and every other branch of modern mathematics − are defined in terms of sets, and have their logical basis in set theory.
EXERCISE 1
a![]() A = { 0, 16, 32, 48, 64, 80, 96 }.
A = { 0, 16, 32, 48, 64, 80, 96 }.
b![]() The most obvious answer is B = { square numbers less than 30 }.
The most obvious answer is B = { square numbers less than 30 }.
c![]() No, because I don’t know precisely enough what ‘close to’ means.
No, because I don’t know precisely enough what ‘close to’ means.
EXERCISE 2
| a | i | A = { 10 002, 10 004, … , 19 998 } is finite. |
||||||
| b | i | This set is infinite. | ii | | S | = 1. |
||||
| iii | | S | = 0. | iv | | S | = 100. | |||||
| c | F =   , ,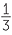 , ,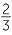 , , , , , ,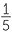 , , , ,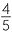 , , , , , , , ,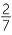 , , , ,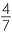 , , , ,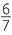 , ,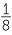 , , , , , ,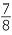 , ,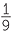 , ,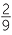 , ,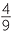 , , , , , ,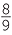  , so | F | = 27. , so | F | = 27. |
|||||||
EXERCISE 3
| a | i | { squares } ⊆ { rectangles }. | ii | { rectangles } ⊆ { rhombuses }. | ||||
| b | i | All multiples of 6 are even. | ii | Not all squares are even. | ||||
| c | i | If a whole number is a multiple of 6, then it is even. | ||||||
| ii | If a whole number is a square, then it may not be even. | |||||||
| d | i | 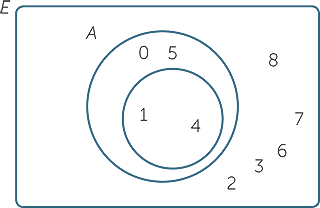 |
||
| ii | 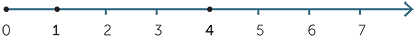 |
|||
EXERCISE 4
| a−d | 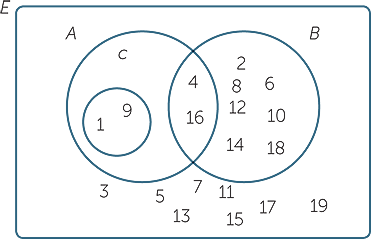 |
EXERCISE 5
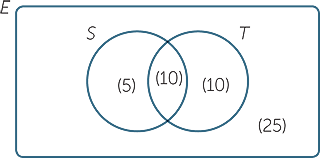
The union S ∪ T has 25 elements, whereas S has 15 elements and T has 20 elements, so the overlap S ∩ T has 10 elements.
Hence the region of S outside S ∩ T has 5 elements, and the region of T outside S ∩ T has 10 elements. Hence the outer region has 50 − 25 = 25 elements.
c![]() From the diagram, | S ∩ T | = 10 and | S ∪ Tc | = 40.
From the diagram, | S ∩ T | = 10 and | S ∪ Tc | = 40.
EXERCISE 6
Since only 18 people are involved in swimming or fishing and 15 + 12 = 27, there are 9 people who go swimming and fishing.
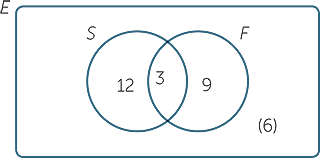
EXERCISE 7
a![]() 9
9![]() b
b![]() 10
10 ![]() c
c![]() 12
12 ![]() d
d![]() 168
168 ![]() e
e![]() 159
159
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()



