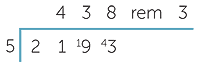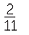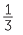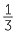The Improving Mathematics Education in Schools (TIMES) Project
- An understanding of the Hindu-Arabic notation and place value as applied to whole numbers (see the module Using Place Value to Write Numbers).
- An understanding of, and fluency with, forwards and backwards skip-counting.
- An understanding of, and fluency with, addition, subtraction and multiplication, including the use of algorithms.
- Experience of division as sharing.
- An appreciation of division as calculating the 'umber of copies' of one whole
number in another. - Knowledge of simple multiplication and division facts.
Division is the last of the arithmetic operations to be introduced in primary school and, technically, the most challenging.
Division answers questions such as:
- How many apples will each friend get if four friends share 24 apples equally
between them? - If twenty pens are shared between seven children how many does each child receive, and how many are left over?
- If your annual salary is $52 000, how much do you earn per fortnight?
- If 421 children are going on an excursion and each bus can carry 35 children, how many full buses are there and how many children are left over?
Fluency with division is essential in many later topics and can be very useful in daily life. Division problems arise when we try to break up a quantity into groups of equal size and when we try to 'undo multiplications'. Division is also central to the calculations of ratios, proportions, percentages and slopes. Division with remainder is a fundamental idea in the number theory concerned with electronic security and cryptography. More immediately, the development of a solid understanding of arithmetic is essential for the development of later topics such as algebra.
Division always involves splitting a collection or a number of things into a number of equal parts, but there are many contrasting situations that can all be described by ‘division’. Before introducing the standard algorithm for division, it is worthwhile discussing some of these situations under the three headings:
- Division without remainder,
- Division with remainder,
- Division resulting in a mixed numeral.
Division resulting in a fraction is considered in the module, Fractions.
Here is a simple model of the division 24 ÷ 8.
Question: If I pack 24 apples into boxes, each with 8 apples, how many boxes will there be?
We can visualise the packing process by laying out the 24 apples successively in rows of 8, as in the diagrams below.

The 3 rows in the last array use up all 24 apples, so there will be 3 full boxes, with no apples left over. The result is written in mathematical symbols as
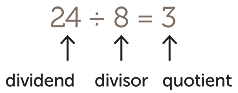
The number 24 is called the dividend (‘that which is to be divided’). The number 8 is called the divisor (‘that which divides’). The number 3 is called the quotient, (from the Latin quotiens meaning ‘how many times’).
Division without remainder can be visualized as skip-counting.
0, 8, 16, 24…
We count in 8s until we reach 24.

EXERCISE 1
a Evaluate 42 ÷ 3 by counting in 3s.
b Evaluate 155 ÷ 31 by counting in 31s.
c Evaluate 140 million ÷ 20 million by counting in 20 millions.
Division without remainder is the inverse of multiplication
 The rectangular array that we produced when we modeled 24 ÷ 8 is exactly the same array that we drew in the module, Multiplication of Whole Numbers to illustrate 24 = 8 × 3
The rectangular array that we produced when we modeled 24 ÷ 8 is exactly the same array that we drew in the module, Multiplication of Whole Numbers to illustrate 24 = 8 × 3
In our example:
- The statement 24 = 8 × 3 means ‘three boxes, each with 8 apples, is 24 apples’, and
- The statement 24 ÷ 8 = 3 means ‘24 apples make up 3 boxes, each with 8 apples’.
Division without remainder is the inverse process of multiplication.
The multiplication statement 24 = 8 × 3 can in turn be reversed to give 24 = 3 × 8 and a second division statement
![]() 24 ÷ 3 = 8
24 ÷ 3 = 8
 which answers the question, ‘What is 24 divided by 3?’.
which answers the question, ‘What is 24 divided by 3?’.
This corresponds to rotating the array by 90°, and regarding it
as made up of 8 rows of 3. It answers the question, ‘If I pack
24 apples into boxes each holding 3 apples, how many boxes
will be required?’.
So the division statement 24 ÷ 8 = 3 now has four equivalent forms:
![]() 24 ÷ 8 = 3 and 24 = 8 × 3 and 24 = 3 × 8 and 24 ÷ 3 = 8
24 ÷ 8 = 3 and 24 = 8 × 3 and 24 = 3 × 8 and 24 ÷ 3 = 8
EXERCISE 2
For each division statement, write down the two corresponding multiplication statements, and the other corresponding division statement.
a ![]() 84 ÷ 12= 7.
84 ÷ 12= 7.
b ![]() 633 ÷ 3 = 211.
633 ÷ 3 = 211.
c ![]() 81 ÷ 9 = 9. What happened in this example, and why?
81 ÷ 9 = 9. What happened in this example, and why?
Two models of division without remainder
 This section is included for teachers because
This section is included for teachers because
children’s questions often concern pairs of
situations similar to those described here.
If we have 24 balloons to share equally, there
are two ways we can share them.
The first way is by asking ‘How many groups?’
For example, if we have 24 balloons and we give 8 balloons each to a number of children, how many children get 8 balloons?
If we split 24 balloons into groups of 8, then 3 children get 8 balloons each.

We say ‘24 divided by 8 is 3’. This is written as 24 ÷ 8 = 3.
We can see this from the array:
![]()
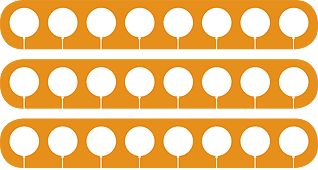
![]() 3 lots of 8 make 24
3 lots of 8 make 24 ![]()
![]()
![]()
![]()
![]() 24 ÷ 8 = 3
24 ÷ 8 = 3
The second way is by asking ‘How many in each group?’ For example, if we share
24 balloons among 8 children, how many balloons does each child receive? We want
to make 8 equal groups. We do this by handing out one balloon to each child. This uses
8 balloons. Then we do the same again.

We can do this 3 times, so each child gets 3 balloons.
Again, we can see this from the multiplication array:
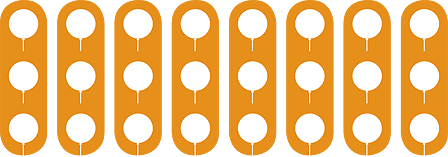
So dividing 24 by 8 is the same as asking ‘Which number do I multiply 8 by to get 24?’
For each division problem, there is usually an associated problem modelling the same division statement. The 'balloons' example above shows how two problems can have the same division statement. One problem with balloons is the associate of the other.
EXERCISE 3
Write down in symbols the division statement, with its answer, for each problem below. Then write down in words the associated problem:
a ![]() If 24 children are divided into 4 equal groups, how many in each group?
If 24 children are divided into 4 equal groups, how many in each group?
b ![]() How many 2-metre lengths of fabric can be cut from a 20 metres length?
How many 2-metre lengths of fabric can be cut from a 20 metres length?
c ![]() If 160 books are divided equally amongst 10 tables, how many on each table?
If 160 books are divided equally amongst 10 tables, how many on each table?
d ![]() How many weeks are there in 35 days?
How many weeks are there in 35 days?
Here is a simple model of 29 ÷ 8.
Question: If I pack 29 apples into boxes, each with 8 apples, how many boxes will there be?
As before, we can visualise the packing process by laying out the 29 apples successively in rows of 8:

We can lay out 3 full rows, but the last row only has five apples, so there will be 3 full boxes and 5 apples left over. The result is written as

The number 5 is called the remainder because there are 5 apples left over. The remainder is always a whole number less than the divisor.
As with division without remainder, skip-counting is the basis of this process:
![]() 0, 8, 16, 24, 32,…
0, 8, 16, 24, 32,…
We locate 29 between successive multiples 24 = 8 × 3 and 32 = 8 × 4 of the divisor 8. Then we subtract to find the remainder 29 − 24 = 5.

We could also have answered the question above by saying, ‘There will be four boxes, but the last box will be 3 apples short.’
This corresponds to counting backwards from 32 rather than forwards from 24, and the corresponding mathematical statement would be
![]() 29 ÷ 8 = 4 remainder (−3).
29 ÷ 8 = 4 remainder (−3).
It is not normal practice at school, however, to use negative remainders, even when the question demands the interpretation corresponding to it. We will always maintain the usual school convention that the remainder is a whole number less than the divisor. Division without remainder can be regarded as division with remainder 0. During the location process, we land on a multiple of the divisor instead of landing between two of them.
For example, 24 ÷ 8 = 3 remainder 0, or more simply, 24÷ 8 = 3, and we say that
![]() 24 is divisible by 8
24 is divisible by 8![]() and that
and that ![]() 8 is a divisor of 24
8 is a divisor of 24![]() or
or ![]() 8 is a factor of 24.
8 is a factor of 24.
EXERCISE 4
a ![]() Locate 60 between multiples of 7, and evaluate 60 ÷ 7.
Locate 60 between multiples of 7, and evaluate 60 ÷ 7.
b ![]() Locate 93 between multiples of 20, and evaluate 93 ÷ 20.
Locate 93 between multiples of 20, and evaluate 93 ÷ 20.
c ![]() Locate 71 432 between multiples of 15 000, and hence evaluate 71 432 ÷ 15 000.
Locate 71 432 between multiples of 15 000, and hence evaluate 71 432 ÷ 15 000.
d ![]() Evaluate 105 ÷ 21 using the location strategy.
Evaluate 105 ÷ 21 using the location strategy.
EXERCISE 5
a ![]() How many doubles tennis games can be formed from 35 players, and how many players are left on the sidelines?
How many doubles tennis games can be formed from 35 players, and how many players are left on the sidelines?
b ![]() How many full cartons of a dozen eggs can be packed from 150 eggs, and how many will be left over?
How many full cartons of a dozen eggs can be packed from 150 eggs, and how many will be left over?
c ![]() How many 20-seater buses are needed to transport 226 people, and how many spare seats are there?
How many 20-seater buses are needed to transport 226 people, and how many spare seats are there?
The corresponding multiplication and addition statement
The 29 apples in our example were packed into 3 full boxes of 8 apples, with 5 left over. We can write this as a division, but we can also write it using a product and a sum,
![]() 29 ÷ 8 = 3 remainder 5
29 ÷ 8 = 3 remainder 5 ![]() or
or ![]() 29 = 8 × 3 + 5
29 = 8 × 3 + 5
We must write this second statement in the form:
![]() dividend = divisior × quotient + remainder
dividend = divisior × quotient + remainder
![]() Note that 29 = 3 × 9 + 2
Note that 29 = 3 × 9 + 2 ![]() is the statement when dividing by 3
is the statement when dividing by 3
So for division with remainder there is a corresponding statement with a multiplication followed by an addition, which is more complicated than division without remainder.
EXERCISE 6
a![]() The first 100 days of a US presidency are regarded as crucial. Express 100 days in weeks and days. Then write down the corresponding division statement and the corresponding product-and-sum statement.
The first 100 days of a US presidency are regarded as crucial. Express 100 days in weeks and days. Then write down the corresponding division statement and the corresponding product-and-sum statement.
b![]() A computer routine takes 10 minutes and 13 seconds. Express this time in seconds. Then write down the corresponding product-and-sum statement and the corresponding division statement.
A computer routine takes 10 minutes and 13 seconds. Express this time in seconds. Then write down the corresponding product-and-sum statement and the corresponding division statement.
EXERCISE 7
a![]() Rewrite 80 ÷ 12 = 6 remainder 8 using a product and a sum.
Rewrite 80 ÷ 12 = 6 remainder 8 using a product and a sum.
b![]() Write down 80 ÷ 6 and relate it to the answer to part a.
Write down 80 ÷ 6 and relate it to the answer to part a.
Two models of division with remainder
As before, problems involving division with remainder usually have an associated problem modelling the same division statement. Continuing with our example of
![]() 29 ÷ 8 = 3 remainder 5:
29 ÷ 8 = 3 remainder 5:
Question: How many bags of 8 apples can I make from 29 apples and how many are left over?
Question: I have 29 apples and 8 boxes. How many apples should I put in each box so that there is an equal number of apples in each box and how many are leftover?
The following two associated questions model 63 ÷ 10 = 6 remainder 3.
Question: If I have 63 dollar coins, and ten people to give them to, how many coins does each person get if they are to each have the same number of coins? How many are left over?
Question: If I have 63 dollar coins, how many $10 books can I buy and how many dollars do I have left over?
EXERCISE 8
Answer each question in words, then write down an associated problem and answer it.
a ![]() How many 7-person rescue teams can be formed from 90 people?
How many 7-person rescue teams can be formed from 90 people?
b ![]() How many 5-seater cars are needed to transport 43 people, and how many spare seats are there?
How many 5-seater cars are needed to transport 43 people, and how many spare seats are there?
Division resulting in a mixed numeral
Division resulting in a mixed numeral requires an understanding of fractions, particularly cancelling fractions, because cancelling is often needed for the final result. It is therefore usual for students to learn division with remainder first, and then to learn division resulting in a mixed numeral in the course of learning fractions. It is important to understand, however, that both ways of expressing the answer are equally important, and both are required, depending on the problem.
Here is a simple model of 29 ÷ 8 = 3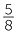 .
.
Question: Divide 29 apples amongst 8 people, cutting up some apples if necessary.
Answer: First, we give 3 apples to each person. This uses up 24 apples, with 5 apples left over.
Now we take each of the five remaining apples in turn, cut it up into eight equal pieces, called eighths, and give one piece to each person. At the end of the process, each person has 3 apples, and 5 eighths of an apple. Using the mixed numeral 3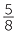 , we say that each person has 3
, we say that each person has 3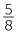 apples, and write the result as
apples, and write the result as
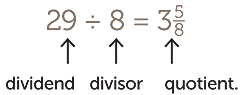
The quotient is 3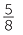 , which is no longer a whole number. We have had to move from whole numbers to the larger system of fractions (non-negative rational numbers) in order to solve the problem.
, which is no longer a whole number. We have had to move from whole numbers to the larger system of fractions (non-negative rational numbers) in order to solve the problem.
This example, with its small change in wording, shows that it depends on the way the question is asked whether the answer should be expressed in terms of quotient and remainder, or as a mixed numeral. For example, here are two associated questions, where one requires a quotient−remainder answer, and the other requires a mixed numeral answer.
Question: How many 40cm lengths can be cut from 450cm of tape?
Question: If 450cm of fabric is cut into 40 equal lengths, how long is each length?
First, we locate 450 between 440 = 40 × 11 and 480 = 40 × 12. Hence
![]() 450 ÷ 40 = 11 remainder 10 or 450 ÷ 40 = 11
450 ÷ 40 = 11 remainder 10 or 450 ÷ 40 = 11 = 11
= 11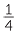
where the mixed numeral 11 simplifies to 11
simplifies to 11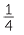 .
.
- The answer to the first question is, ‘There will be eleven 40cm lengths, with 10cm left over.’
- The answer to the second question is, ‘Each length is 11
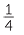 cm.’
cm.’
EXERCISE 9
| a | i | How many days and hours in 60 hours? |
| ii | If a period of 60 hours is divided into 24 equal periods, how long is each period? | |
| b | i | How many 120g packets can be made up from 2000g of coffee? |
| ii | If 2000g of coffee is divided into 120 packets, how much is in each packet? | |
| c | i | If hospitals cost $20 000 000 each, how many can be built with $208 000 000? |
| ii | If the Federal Government spends $208 000 000 on hospitals and pays for this from the money it receives from income tax, how much on average will it cost each of the 20 000 000 Australian citizens in taxes? |
Division resulting in a mixed numeral is the inverse of multiplication
We divided 29 apples amongst 8 people, and each person received 3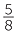 apples.
apples.
Note that adding up all the 8 shares of 3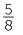 apples gives 29 apples. We thus have
apples gives 29 apples. We thus have
two corresponding statements:
![]() 29 ÷ 8 = 3
29 ÷ 8 = 3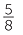
![]() and
and ![]() 29 = 8 × 3
29 = 8 × 3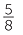
![]() or
or ![]() 29 = 3
29 = 3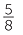 × 8
× 8
The situation is straightforward once again, and division resulting in a mixed numeral is the inverse of multiplication.
As with division without remainder, we have a second division statement, 29 ÷ 3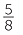 = 8 but this will not be relevant to most students at this stage because division by a mixed numeral requires a more mature understanding of fractions − see the later module Fractions.
= 8 but this will not be relevant to most students at this stage because division by a mixed numeral requires a more mature understanding of fractions − see the later module Fractions.
EXERCISE 10
Rewrite each division statement using a mixed numeral, cancelled if necessary.
Then rewrite it as a multiplication statement.
a ![]() 35 ÷ 11 = 3 remainder 2.
35 ÷ 11 = 3 remainder 2.
b ![]() 70 ÷ 8 = 8 remainder 6.
70 ÷ 8 = 8 remainder 6.
c ![]() 40 000 ÷ 3000 = 13 remainder 1000.
40 000 ÷ 3000 = 13 remainder 1000.
The standard division algorithm
There is only one standard division algorithm, despite its different appearances. The algorithm can be set out as a ‘long division’ calculation to show all the steps, or as a ‘short division’ algorithm where only the carries are shown, or with no written working at all.
Setting the calculation out as a long division
We could set the calculation out as follows:
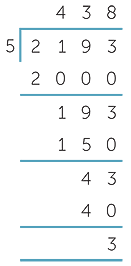 5 × 400 = 2000, then subtract 2000 from 2193
5 × 400 = 2000, then subtract 2000 from 2193
5 × 30 = 150, then subtract 150 from 193
5 × 8 = 40, then subtract 40 from 43
The standard ‘long division’ setting-out, however, allows place value to work for us even more efficiently, by working only with the digits that are required for each particular division. At each step another digit is required − this is usually called ‘bringing down the next digit’.
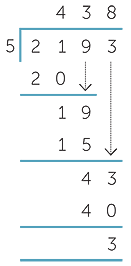 Divide 21 by 5.
Divide 21 by 5.
5 × 4 = 20, then subtract 20 from 21.
Bring down the 9, and divide 19 by 5.
5 × 3 = 15, then subtract 15 from 19.
Bring down the 3, and divide 43 by 5.
5 × 8 = 40, then subtract 40 from 43.
Hence 2193 ÷ 5 = 438 remainder 3. (Always gather the calculation up into a conclusion.)
The placing of the digits in the top line is crucial. The first step is ‘5 into 21 goes 4’, and the digit 4 is placed above the digit 1 in 21.
Setting the calculation out as a short division
Once the steps have been mastered, many people are comfortable doing each multiplication− subtraction step mentally and writing down only the carry. The calculation then looks like this:
|
|
We say, |
‘5 into 21 goes 4, remainder 1’. |
EXERCISE 11
Solve each problem first using long division setting-out, then using short division setting-out.
a ![]() Express 42 897 days as weeks and days.
Express 42 897 days as weeks and days.
b ![]() Express 11 447 months as years and months.
Express 11 447 months as years and months.
Zeroes in the dividend
Zeroes will cause no problems provided only that all the digits are kept strictly in their correct columns. This same principle is fundamental to all algorithms that rely on place value.
The example below shows the long division and short division calculations for
![]() 16 070 ÷ 8 = 2008 remainder 6
16 070 ÷ 8 = 2008 remainder 6
 We twice had to bring down the digit 0, and two of the divisions resulted in a quotient of 0.
We twice had to bring down the digit 0, and two of the divisions resulted in a quotient of 0.
Long division by numbers with two or more digits
The one problem with the division algorithm is that we need to know the first 9 multiples of the divisor. All of us quickly run out of known multiplication tables, and to divide by any other numbers, begin by writing down the first 9 multiples of the divisor.
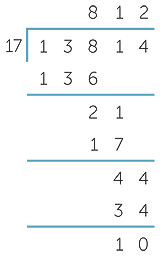 Here is the setting-out of the calculation for 13 814 ÷ 17
Here is the setting-out of the calculation for 13 814 ÷ 17
We begin by writing down the first 10 multiples of 17,
17, 34, 51, 68, 85, 102, 119, 136, 153, 170.
Of course in any given problem we may not need all 10 multiples.
So 13 814 ÷ 7 = 812 rem 10
EXAMPLE
Find 97 958 ÷ 123.
Solution
|
|
123 × 1 = 123 |
That is, 97 958 ÷ 123 = 796 remainder 50.
Note: Once the table is finished, the only arithmetic to be done is subtraction.
EXERCISE 12
| a | Write down the first 9 multiples of 24, then convert 10 000 hours to days and hours. |
| b | A kilobyte is 210 = 1024 bytes (not 1000 bytes). Write down the first 9 multiples of 1024, then find how many kilobytes and bytes there are in 1 000 000 bytes. |
Using the calculator for division with remainder
People often say that division is easily done on the calculator. Division with remainder, however, requires some common sense to sort out the answer.
EXAMPLE
Use the calculator to convert 350 minutes to hours and minutes.
Solution
We can see that 350 minutes = 300 minutes + 50 minutes = 5 hours and 50 minutes.
With a calculator in decimal or approximate mode using the division key: Enter 350 ÷ 60, and the answer is 5.833333… hours. Then subtract 5 to get 0.833333…, and multiply by 60 to convert to 50 minutes, giving the answer 5 hours and 50 minutes.
Calculator assistance may be extremely useful with larger numbers, but understanding of division is essential to interpret the calculator display This phenomenon is common to many similar situations in mathematics.
EXERCISE 13
a ![]() A radar initially pointed north, then rotated clockwise for a few hours. When it was stopped for a calibration check, it registered that it had turned through 53 550°.
A radar initially pointed north, then rotated clockwise for a few hours. When it was stopped for a calibration check, it registered that it had turned through 53 550°.
Use the division button on a calculator to find how many full revolutions it had turned, and its true bearing now.
b ![]() Convert 1 000 000 hours to days and hours using the division button on the calculator.
Convert 1 000 000 hours to days and hours using the division button on the calculator.
Division by successive factors
It is often said that, ‘To divide by 60, you divide by 10 and then by 6’. This works well for division without remainder, but runs into serious problems with division with remainder and division resulting in a mixed numeral.
Suppose we want to express 300 minutes in hours. We write
![]() 300 ÷ 60 = (300 ÷ 10) ÷ 6 = 30 ÷ 6 = 5, so 300 minutes is 5 hours.
300 ÷ 60 = (300 ÷ 10) ÷ 6 = 30 ÷ 6 = 5, so 300 minutes is 5 hours.
Division by successive factors
- Division by succesive factors is extremely useful for division without remainder.
- Division by succesive factors does not work for division with remainder.
- You will need fluency in fractions to divide by succesive factors for division resulting in a mixed numeral.
EXERCISE 14
a ![]() Divide 2184 by 84 by first dividing by 7 and then by 12.
Divide 2184 by 84 by first dividing by 7 and then by 12.
b ![]() Find how many revolutions in 1890° by first finding how many right angles there
Find how many revolutions in 1890° by first finding how many right angles there
are in 1890°.
c ![]() Convert 372 hours to days and hours by dividing by 12 and then by 2.
Convert 372 hours to days and hours by dividing by 12 and then by 2.
Dividing by 4, 8, 16, …
Because 4 = 2 × 2 and 8 = 2 × 2 × 2, we can divide by 4 and 8, and by all powers of 2,
by successive halving.
To divide by 4, halve and halve again. To divide by 8, halve, halve, and halve again.
For example, to divide 628 by 4, 628 ÷ 4 = (628 ÷ 2) ÷ 2 = 314 ÷ 2 = 157
To divide 976 by 8, 976 ÷ 8 = (976 ÷ 2) ÷ 2 ÷ 2 = (488 ÷ 2) ÷ 2 = 244 ÷ 2 = 122
EXERCISE 15
Use repeated halving to evaluate
|
a |
246 ÷ 4 |
b |
368 ÷ 8 |
|||
|
c |
163 ÷ 8 |
d |
12 048 ÷ 16 |
Division by 5, 25, 125, …
Because 5 = 10 ÷ 2, and 25 = 100 ÷ 4, there is a very effective way to divide by 5 and 25 and all powers of 5.
- To divide by 5, divide by 10 and then double.
- To divide by 25, divide by 100 and then double and double again.
Decimals are best used for the working. For example, to divide 245 and 382 by 5,
245 ÷ 5 = (245 ÷ 10) × 2 = 24.5 × 2 = 49
382 ÷ 5 = (382 ÷ 10) × 2 = 38.2 × 2 = 76.4
and to divide 825 and 1134 by 25,
825 ÷ 25 = (825 ÷ 100) × 2 × 2 = 8.25 × 2 × 2 = 16.5 × 2 = 33
1134 ÷ 25 = (1134 ÷ 100) × 2 × 2 = 11.34 × 2 × 2 = 22.68 × 2 = 45.36
EXERCISE 16
a ![]() Divide 585 and 914 by 5.
Divide 585 and 914 by 5.
b ![]() Divide 3175 and 2105 by 25.
Divide 3175 and 2105 by 25.
Expanding brackets − the distributive law
To pack 96 apples into boxes, each holding 8 apples, we could do it in two stages.
First pack apples into 10 boxes, then pack the remaining 16 apples into 2 boxes
![]() (80 + 16) ÷ 8 = 80 ÷ 8 + 16 ÷ 8;
(80 + 16) ÷ 8 = 80 ÷ 8 + 16 ÷ 8; ![]() so
so![]() 96 ÷ 8 = 12.
96 ÷ 8 = 12.
To pack 100 apples into boxes, each holding 8 apples, we could do it in two stages.
First pack 80 apples into 10 boxes, then pack the remaining 20 apples into 2 boxes, leaving 4 apples remaining. In symbols, we write this as
![]() (80 + 20) ÷ 8 = 80 ÷ 8 + 20 ÷ 8 = 10 + 2 rem 4
(80 + 20) ÷ 8 = 80 ÷ 8 + 20 ÷ 8 = 10 + 2 rem 4![]() so
so![]() 100 ÷ 8 = 12 remainder 4.
100 ÷ 8 = 12 remainder 4.
This expansion of brackets is called the distributive law of division over addition.
This law can be useful in other contexts, provided that the remainders can be handled correctly. For example, now that we know 100 apples will fill 12 boxes with 4 apples left over, we can see that 500 apples will fill 60 boxes with 20 left over, which gives 22 boxes and 4 left over.
The following exercise gives two examples where such manoeuvre with the remainder can replace a written calculation with mental calculations.
EXERCISE 17
a ![]() A computer macro runs for 200 seconds. Express this in minutes and seconds, and hence find how long it will take to run 7 versions of the macro in succession.
A computer macro runs for 200 seconds. Express this in minutes and seconds, and hence find how long it will take to run 7 versions of the macro in succession.
b ![]() A training company runs a 25-day programme. Express this time in weeks and days, and hence find how many weeks and days six successive programmes will run.
A training company runs a 25-day programme. Express this time in weeks and days, and hence find how many weeks and days six successive programmes will run.
A well-known version of this approach is used when we divide numbers that are close to a known multiple of the divisor. For example, to divide 7010 by 7 and 5990 by 6,
![]() 7010 ÷ 7 =7000 ÷ 7 + 10 ÷ 7 = 1000 + 10 ÷ 7 = 1001 rem 3
7010 ÷ 7 =7000 ÷ 7 + 10 ÷ 7 = 1000 + 10 ÷ 7 = 1001 rem 3
![]() 5988 ÷ 6 = 6000 ÷ 6 − 12 ÷ 6 = 1000 − 2 = 998
5988 ÷ 6 = 6000 ÷ 6 − 12 ÷ 6 = 1000 − 2 = 998
Order and brackets cannot be ignored
When multiplying two numbers, the order is unimportant. For example,
![]() 3 × 8 = 8 × 3 = 24.
3 × 8 = 8 × 3 = 24.
Recall that this is called the commutative law for multiplication.
When dividing number, however, the order is crucial. For example,
![]() 20 ÷ 4 = 5, but 4 ÷ 20 =
20 ÷ 4 = 5, but 4 ÷ 20 = 
This means that division is not commutative.
To visualise this calculation, 20 people living in 4 homes means each home has on average 5 people, whereas 4 people living in 20 homes means each home has on average  people.
people.
Similarly, when multiplying numbers, the use of brackets is unimportant. For example,
![]() (3 × 4) × 5 = 12 × 5 = 60
(3 × 4) × 5 = 12 × 5 = 60 ![]() and
and ![]() 3 × (4 × 5) = 3 × 20 = 60.
3 × (4 × 5) = 3 × 20 = 60.
When dividing numbers, however, the use of brackets is crucial. For example,
![]() (24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3;
(24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3; ![]() but
but ![]() 24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12
24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12
This illustrates that multiplication is associative but division is not associative.
The division algorithm uses multiplication and subtraction. As such, division demands that we synthesise a lot of prior knowledge. This is what makes division challenging, and for many students it is their first taste of multi-layered processes. The ability to reflect on what you know, and implement it within a new, higher-level process is one of the generic mathematical skills that division helps to develop.
The implementation of the division algorithm is typically a multi-step process, and as such it helps to develop skills that are invaluable when students move on to algebra. The link to factors is also critical in later years.
Just as the history of number is really all about the development of numerals, the history of division is mainly the history of the processes people have used to perform calculations.
The earliest recorded example of a division implemented algorithmically is a Sunzi division dating from 400AD in China. Essentially the same process reappeared in the book of al Kwarizmi in 825AD and the modern-day equivalent is known as Galley division. It is, in essence, equivalent to modern-day long division. However, it is a wonderful example of how notation can make an enormous difference. Galley division is hard to follow and leaves the page a mess compared to the modern layout.
The layout of the long division algorithm varies between cultures.
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
Knowing and Teaching Elementary Mathematics: teachers’ understanding of fundamental mathematics in China and the United States. Liping Ma, Mahwah, N.J.: Lawrence Erlbaum Associates, (1999)
Exercise 1
a![]() 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42. Hence 42 ÷ 3 = 14.
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42. Hence 42 ÷ 3 = 14.
b![]() 31, 62, 93, 124, 155. Hence 155 ÷ 31 = 5.
31, 62, 93, 124, 155. Hence 155 ÷ 31 = 5.
c![]() 20 million, 40 million, 60 million, 80 million, 100 million, 120 million, 140 million. Hence 140 000 000 ÷ 20 000 000 = 7.
20 million, 40 million, 60 million, 80 million, 100 million, 120 million, 140 million. Hence 140 000 000 ÷ 20 000 000 = 7.
Exercise 2
a![]() 84 = 12 × 7, 84 = 7 × 12 and 84 ÷ 7 = 12.
84 = 12 × 7, 84 = 7 × 12 and 84 ÷ 7 = 12.
b![]() 633 = 3 × 211, 633 = 211 × 3 and 633 ÷ 211= 3.
633 = 3 × 211, 633 = 211 × 3 and 633 ÷ 211= 3.
c![]() 81 = 9 × 9 and 81 ÷ 9 = 9. There is only one multiplication and one division statement since 81 = 92.
81 = 9 × 9 and 81 ÷ 9 = 9. There is only one multiplication and one division statement since 81 = 92.
Exercise 3
a![]() 24 ÷ 4 = 6. If 24 children are divided into groups of 4, how many groups are there?
24 ÷ 4 = 6. If 24 children are divided into groups of 4, how many groups are there?
b![]() 20 ÷ 2 = 10. If 20 metres of fabric is divided into two equal pieces, how long is each piece?
20 ÷ 2 = 10. If 20 metres of fabric is divided into two equal pieces, how long is each piece?
c![]() 160 ÷ 10 = 16. If 160 books are placed on tables with 10 on each, how many tables are needed?
160 ÷ 10 = 16. If 160 books are placed on tables with 10 on each, how many tables are needed?
d![]() 35 ÷ 7 = 5. If a 35-day period is divided into 7 equal periods, how long is each period?
35 ÷ 7 = 5. If a 35-day period is divided into 7 equal periods, how long is each period?
Exercise 4
a![]() 60 is between 56 = 7 × 8 and 63 = 7 × 9, so 60 ÷ 7 = 8 remainder 4.
60 is between 56 = 7 × 8 and 63 = 7 × 9, so 60 ÷ 7 = 8 remainder 4.
b![]() 93 is between 80 ÷ 20 = 4 and 100 = 20 × 5, so 93 ÷ 20 = 4 remainder 13.
93 is between 80 ÷ 20 = 4 and 100 = 20 × 5, so 93 ÷ 20 = 4 remainder 13.
c![]() 71 432 is between 60 000 = 15 000 × 4 and 75 000 = 15 000 × 5,
71 432 is between 60 000 = 15 000 × 4 and 75 000 = 15 000 × 5,
so 71 432 ÷ 15 000 = 4 remainder 11 432.
d![]() 105 = 21 × 5 is actually a multiple of 21, so 0; 105 ÷ 21 = 5.
105 = 21 × 5 is actually a multiple of 21, so 0; 105 ÷ 21 = 5.
Exercise 5
a![]() 35 ÷ 4 = 8 remainder 3, so there are 8 games, with 3 players sidelined.
35 ÷ 4 = 8 remainder 3, so there are 8 games, with 3 players sidelined.
b![]() 150 ÷ 12 = 12 remainder 6, so there will be 12 full cartons, with 6 eggs left over.
150 ÷ 12 = 12 remainder 6, so there will be 12 full cartons, with 6 eggs left over.
c![]() 226 ÷ 20 = 11 remainder 6, so there must be 12 buses, with 14 spare seats.
226 ÷ 20 = 11 remainder 6, so there must be 12 buses, with 14 spare seats.
Exercise 6
a![]() 100 days is 14 weeks and 2 days. 100 ÷ 7 = 14 remainder 2 and 100 = 7 × 14 + 2:
100 days is 14 weeks and 2 days. 100 ÷ 7 = 14 remainder 2 and 100 = 7 × 14 + 2:
b![]() 10 minutes and 13 seconds is 613 seconds. 613 = 60 × 10 + 13 and 613 ÷ 60 = 10 remainder 13:
10 minutes and 13 seconds is 613 seconds. 613 = 60 × 10 + 13 and 613 ÷ 60 = 10 remainder 13:
Exercise 7
a![]() 80 ÷ 12 = 6 remainder 8 can be rewritten as 80 = 12 × 6 + 8.
80 ÷ 12 = 6 remainder 8 can be rewritten as 80 = 12 × 6 + 8.
b![]() This gives 80 ÷ 6 = 13 remainder 2.
This gives 80 ÷ 6 = 13 remainder 2.
Exercise 8
a![]() Twelve 7-person rescue teams can be formed, with 6 people to spare. How many people will be in 7 equal groups formed from 90 people? There will be 12 people in each group, with 6 left over.
Twelve 7-person rescue teams can be formed, with 6 people to spare. How many people will be in 7 equal groups formed from 90 people? There will be 12 people in each group, with 6 left over.
b![]() Nine 5-seater cars are needed, and there will be two spare seats. How many people will be in 5 equal groups formed from 43 people? There will be 8 groups, with
3 people left over.
Nine 5-seater cars are needed, and there will be two spare seats. How many people will be in 5 equal groups formed from 43 people? There will be 8 groups, with
3 people left over.
Exercise 9
| a | First, we locate 60 between 48 = 24 × 2 and 72 = 24 × 3. Hence 60 ÷ 24 = 2 remainder 12 or 60 ÷ 24 = 2 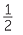 : : |
|
| i | 60 hours is 2 days and 12 hours. | |
| ii | Each of the 24 periods will be 2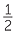 hours. hours. |
|
| b | First, we locate 2000 between 1920 = 120 × 16 and 2040 = 120 × 17. Hence 2000 ÷ 120 = 16 remainder 80 or 2000 ÷ 120= 16 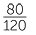 = 16 = 16 . . |
|
| i | There will be 16 packets each of 120g, with 80g left over. | |
| ii | Each of the 120 packets will contain 16 g of coffee. g of coffee. |
|
| c | First, we locate 208M between 200M = 20M × 10 and 210M = 20M × 11. Hence 208M ÷ 20M = 10 remainder 8M or 208M ÷ 20M = 10  = 10.4. = 10.4. |
|
| i | We can build 10 hospitals, with $8 000 000 left over. | |
| ii | Each Australian on average will pay $10.40. | |
Exercise 10
a |
35 ÷ 11 = 3 |
and | 35 = 11 × 3 |
|||
| b | 70 ÷ 8 = 8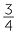 |
and | 70 = 8 × 8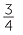 |
|||
c |
40 000 ÷ 3000 = 13 |
and | 40 000 = 3000 × 13 |
Exercise 11
a
![]()
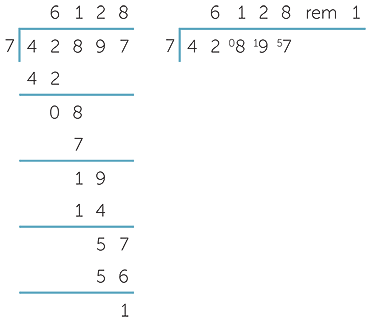
![]() Hence 42 897 days is 6128 weeks and 1 day.
Hence 42 897 days is 6128 weeks and 1 day.
b
![]()
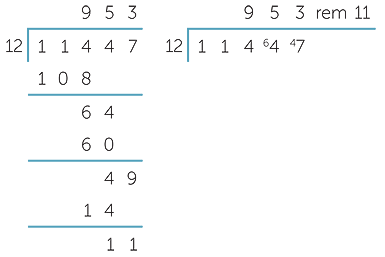
![]() Hence 11 445 months is 953 years and 11 months
Hence 11 445 months is 953 years and 11 months
Exercise 12
a![]() 24, 48, 72, 96, 120, 144, 168, 192, 216
24, 48, 72, 96, 120, 144, 168, 192, 216
![]()
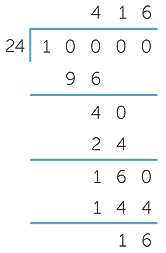
Hence 1 000 000 hours is 416 days and 16 hours.
b![]() 1024, 2048, 3072, 4096, 5120, 6144, 7168, 8192, 9216, 10 240
1024, 2048, 3072, 4096, 5120, 6144, 7168, 8192, 9216, 10 240
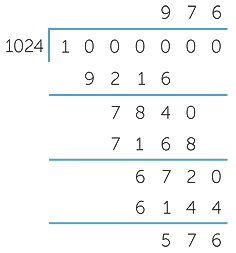
Hence 1 000 000 btyes is not 1000 kilobytes, but is 976 kilobytes and 576 bytes.
Exercise 13
a![]() Using the division button, 53 550 = 148
Using the division button, 53 550 = 148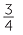 = 148
= 148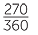 ; so 53 550 = 148 revolutions
; so 53 550 = 148 revolutions
and 270°. So it had turned 148 full revolutions, and was now pointing west.
b![]() Using the division button, 1 000 000 ÷ 24 = 41 666.666… = 41 666
Using the division button, 1 000 000 ÷ 24 = 41 666.666… = 41 666 .
.
Hence 1 000 000 hours is 41 666 days and 16 hours.
Exercise 14
a![]() 2184 ÷ 84 = (2184 ÷ 7) ÷ 12 = 312 ÷ 12 = 26.
2184 ÷ 84 = (2184 ÷ 7) ÷ 12 = 312 ÷ 12 = 26.
b![]() 1890 ÷ 90 = 21, so 1890° is 21 right angles, which is 5
1890 ÷ 90 = 21, so 1890° is 21 right angles, which is 5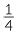 revolutions.
revolutions.
c![]() 372 ÷ 24 = (372 ÷ 12) ÷ 2 = 31 ÷ 2 = 15
372 ÷ 24 = (372 ÷ 12) ÷ 2 = 31 ÷ 2 = 15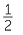 . Hence 372 hours is 15 days and 12 hours.
. Hence 372 hours is 15 days and 12 hours.
Exercise 15
a![]() 246 ÷ 4 = (246 ÷ 2) ÷2 = 123 ÷ 2 = 61
246 ÷ 4 = (246 ÷ 2) ÷2 = 123 ÷ 2 = 61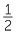
b![]() 368 ÷ 8 = ((368 ÷ 2) ÷ 2) ÷ 2 = (184 ÷ 2) ÷ 2 = 92 ÷ 2= 46.
368 ÷ 8 = ((368 ÷ 2) ÷ 2) ÷ 2 = (184 ÷ 2) ÷ 2 = 92 ÷ 2= 46.
c![]() ((163 ÷ 2) ÷ 2) ÷ 2 = (81.5 ÷ 2) ÷ 2 = 40.75 ÷ 2= 20.375.
((163 ÷ 2) ÷ 2) ÷ 2 = (81.5 ÷ 2) ÷ 2 = 40.75 ÷ 2= 20.375.
d![]() 12 048 ÷ 16 = (((12048 ÷ 2) ÷ 2) ÷ 2 = (((6024 ÷ 2) ÷ 2) ÷ 2 = (3012 ÷ 2) ÷ 2
12 048 ÷ 16 = (((12048 ÷ 2) ÷ 2) ÷ 2 = (((6024 ÷ 2) ÷ 2) ÷ 2 = (3012 ÷ 2) ÷ 2
= 1506 ÷ 2 = 753.
Exercise 16
a![]() 585 ÷ 5 = 117 and 914 ÷ 5 = 182.8.
585 ÷ 5 = 117 and 914 ÷ 5 = 182.8.
b![]() 3175 ÷ 25 = 127 and 2105 ÷ 25 = 84.2.
3175 ÷ 25 = 127 and 2105 ÷ 25 = 84.2.
Exercise 17
a![]() Each process takes 3 minutes and 20 seconds. The combined process will take
Each process takes 3 minutes and 20 seconds. The combined process will take
21 minutes and 140 seconds, which is 23 minutes and 20 seconds.
b![]() Each programme runs for 3 weeks and 4 days. The 6 programmes together run for
Each programme runs for 3 weeks and 4 days. The 6 programmes together run for
18 weeks and 24 days, which is 21 weeks and 3 days.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()