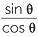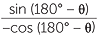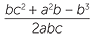The Improving Mathematics Education in Schools (TIMES) Project
- Familiarity with the content of the module, Introductory Trigonometry.
- Familiarity with basic coordinate geometry.
- Facility with simple algebra, formulas and equations.
- Familiarity with surds.
In the module, Introductory Trigonometry, we showed that if we know the angles and one side in a right-angled triangle we can find the other sides using the trigonometric ratios sine, cosine and tangent. Similarly, knowing any two of the sides in a right-angled triangle enables us to find all the angles.
Not all triangles contain a right-angle. We can relate sides and angles in an arbitrary triangle using two basic formulas known as the sine rule and the cosine rule.
Armed with these we can solve a greater range of problems in two dimensions and extend these ideas to three-dimensional problems as well. This is an essential tool for surveyors and civil engineers.
It soon becomes apparent that in some cases we need to be able to define the trigonometric ratio of an obtuse angle. This allows us to deal with a broader range of problems and applications. It will also provide the model for extending the definition of the trigonometric ratios to any angle. This idea will be picked up in the module, The Trigonometric Functions.
In the module, Introductory Trigonometry − Years 9-10, we defined the three standard trigonometric ratios sine, cosine and tangent of an angle θ, called the reference angle,
in a right-angled triangle.
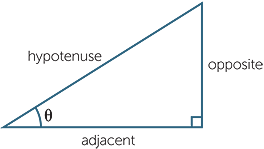
These are defined by:
sin θ =  , cos θ =
, cos θ =  , tan θ =
, tan θ =  , where 0° < θ < 90°.
, where 0° < θ < 90°.
Students should learn these ratios thoroughly. One simple mnemonic that might assist them is SOH CAH TOA, consisting of the first letter of each ratio and the first letter of the sides making up that ratio.
In a right-angled triangle, the other two angles are complements of each other. As the diagram below shows, the side opposite one of these angles is adjacent to the other.
![]()
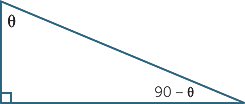
Thus, it can be seen that,
![]() sin θ = cos (90° − θ)
sin θ = cos (90° − θ) ![]() and
and ![]() cos θ = sin (90° − θ) if 0° < θ < 90°
cos θ = sin (90° − θ) if 0° < θ < 90°
The cosine (co-sine) is so named since the cosine of an angle is the sine of its complement.
These ratios can be used to find sides and angles in right-angled triangles.
EXAMPLE
Find, correct to two decimal places, the value of the pronumeral in each triangle.
| a |  |
b | 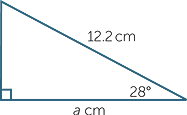 |
Solution
| a | sin 15° | =  |
|
=  |
|||
| x | = 8 × sin 15° | ||
| ≈ 2.07 | (correct to two decimal places) | ||
| b | cos 28° | =  |
|
=  |
|||
| a | = 12.2 × cos 28° | ||
| ≈ 10.77 | (correct to two decimal places) | ||
EXAMPLE
Calculate the value of θ, correct to one decimal place.
| a | 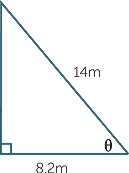 |
b |  |
Solution
| a | cos θ | = 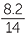 |
|
| So, θ | = cos−1  |
||
| ≈ 54.1° (correct to one decimal place) | |||
| b | tan θ | = 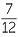 |
|
| So, θ | = tan−1 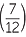 |
||
| ≈ 30.3° (correct to one decimal place) |
Note that for 0 < x < 1 the statement sin-1 x = θ means that sin θ = x. This notation is standard but it is essential that students do not confuse the inverse notation with the usual meaning of the index -1 used in algebra. To help avoid this confusion, it is best to always read sin-1 x as inverse sine of x and tan-1 x as inverse tangent of x.
The trigonometric ratios for the angles 30°, 45° and 60° can be expressed using surds and occur very frequently in introductory trigonometry, in senior mathematics and in calculus. It is thus important for students to become familiar with them.
One way to find them quickly is to sketch the following triangles and then simply write down the ratios.
A right-angled triangle containing a 45° angle will be isosceles, so we choose the two shorter sides to be 1 unit in length and use Pythagoras’ theorem to find the hypotenuse.
For the angles 30° and 60°, we start with an equilateral triangle of side 2 units in length and drop a perpendicular as shown. Simple geometry and Pythagoras’ theorem gives the remaining information as shown in the diagram.
![]()
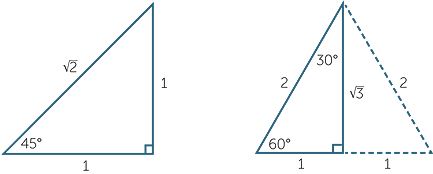
The table of values can now be completed from these diagrams.
| θ | sin θ | cos θ | tan θ |
| 30° | 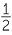
|
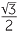
|
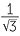
|
| 45° | 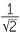
|

|
1 |
| 60° | 
|
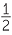
|
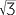
|
There are several deviations from the usual index notation that arise in trigonometry. Students may initially find them confusing.
We write, for example (tan θ) 2 as tan2 θ, (sin θ)3 as sin3 θ and so on. This must not be confused with the inverse notation discussed above. We do not write, for example,
sin-2 θ for (sin θ)-2, since this would confuse the usual meaning of indices with inverses.
EXERCISE 1
a![]() Simplify tan2 30 −
Simplify tan2 30 − 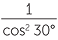 .
.
b![]() The top of a tower has an angle of elevation of 45° from a point on the ground. From a point 100m further on, the angle of elevation is 30°, as shown in the diagram. Find the exact value, x, of the height of the tower.
The top of a tower has an angle of elevation of 45° from a point on the ground. From a point 100m further on, the angle of elevation is 30°, as shown in the diagram. Find the exact value, x, of the height of the tower.
![]()
We can use our knowledge of trigonometry to solve problems in three dimensions.
EXAMPLE
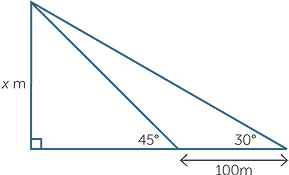
 In the triangular prism opposite, find:
In the triangular prism opposite, find:
a the length CF
b the length BF
c the angle BFC, correct to one decimal place.
Solution
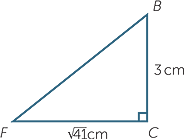
| a | Applying Pythagoras’ theorem to  CEF, CEF, |
|||
| CF2 | = 42 + 52 |
|||
| = 41 | ||||
| Hence | CF | = |
||
| b | Applying Pythagoras’ theorem to  BCF, BCF, |
|||
| BF2 | = 32 + ( |
|||
| = 50 | ||||
| So | BF | = 5 |
||
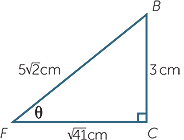
| c | To find the angle BFC, draw  BCF and let BCF and let  BFC = θ. BFC = θ. |
||||
| Now | tan θ | = 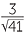 |
|||
| giving | θ | = tan−1  |
|||
| So |  BFC BFC |
≈ 25.1° | (to one decimal place) | ||
EXERCISE 2
Find  CEG in the cube shown below.
CEG in the cube shown below.
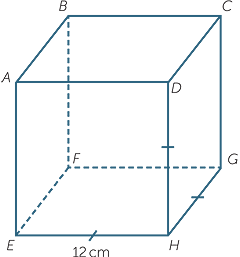
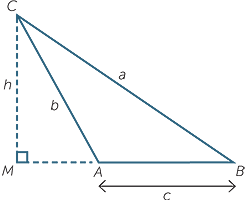
In many applications we encounter triangles that are not right-angled. We can extend our knowledge of trigonometry to deal with these triangles. This is done using two basic formulas, the first of which is called the sine rule.
We will assume, for the moment, that we are dealing with an acute-angled triangle ABC.
As shown in the diagram, we drop a perpendicular CP of length h from C to AB.
![]()
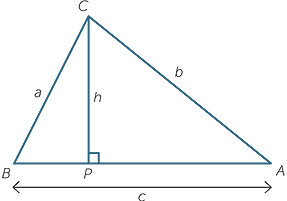
Then in  APC we have sin A =
APC we have sin A = 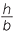 , so h = b sin A.
, so h = b sin A.
Similarly, in  CPB we have sin B =
CPB we have sin B =  , so h = a sin B.
, so h = a sin B.
Equating these two expressions for h we have b sin A = a sin B which we can write as
![]()
 =
= 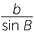 .
.
The same result holds for the side and the angle , so we can write
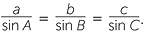
This is known as the sine rule. In words it says: any side of a triangle over the sine of the opposite angle equals any other side of the triangle over the sine of its opposite angle.
We will soon see how to extend this result to obtuse-angled triangles.
EXAMPLE
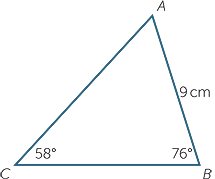 In
In  ABC, AB = 9 cm.
ABC, AB = 9 cm.  ABC = 76° and
ABC = 76° and  ACB = 58°.
ACB = 58°.
Find, correct to two decimal places:
a AC ![]() b BC
b BC
Solution
| a | Apply the sine rule: | ||||
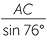 |
= 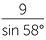 |
||||
| and so | AC | =  |
|||
| ≈ 10.30 cm | (to two decimal places) | ||||
| b | To find BC, we need the angle  CAB opposite it. CAB opposite it. |
||||
 CAB CAB |
= 180° − 58° − 76° | ||||
| = 46° | |||||
| Thus, by the sine rule: | |||||
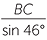 |
= 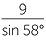 |
||||
| BC | = 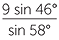 |
||||
| ≈ 7.63 cm | (to two decimal places) | ||||
True bearings were covered in the module, Introductory Trigonometry.
We can now use the sine rule to solve simple surveying problems involving non-right-angled triangles.
EXAMPLE
From the points A and B, 800 metres apart, on a straight North-South road, the bearing of a house is 125°T and 050°T respectively. Find how far each point is from the house, correct to the nearest metre.
Solution
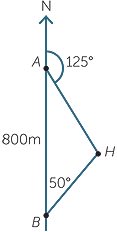 We draw a diagram to represent the information.
We draw a diagram to represent the information.
We can find the angles in  AHB.
AHB.
 HAB HAB |
= 180° − 125° | |
| = 55° | ||
| and |  AHB AHB |
= 180° − 50° − 55° |
| = 75° |
Apply the sine rule to  ABH:
ABH:
 |
=  |
||
| and so | BH | = 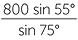 |
|
| ≈ 678.44 m | (to two decimal places) |
Thus B is approximately 678 metres from the house.
| Similarly, |  |
= 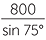 |
|
| and so | AH | = 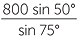 |
|
| ≈ 634.45 m | (to two decimal places) |
Thus A is approximately 634 metres from the house.
EXERCISE 3
From a point at P, west of a building OA, the angle of elevation of the top A of the building OA is 28°. From a point Q 10m further west from P the angle of elevation is 20°. Draw a diagram and then use the sine rule to find the distance AP and hence the exact height of the building. Finally, evaluate the height OA to the nearest centimetre.
The sine rule can be used to find angles as well as sides in a triangle. One of the known sides, however, must be opposite one of the known angles.
EXAMPLE
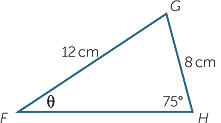 Assuming that all the angles are acute.
Assuming that all the angles are acute.
Find the angle θ in the triangle FGH, to the nearest degree.
Solution
Apply the sine rule to  FGH, FGH, |
|||
 |
=  |
||
| To make the algebra easier, take the reciprocal of both sides. | |||
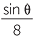 |
= 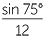 |
||
| Hence | sin θ | = 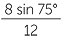 |
|
| = 0.644... | |||
| Hence | θ | = 40° | (to the nearest degree) |
As seen in the example above, it is easier when finding angles, to write the sine rule as  =
=  before substituting in the given information.
before substituting in the given information.
Both the sine rule and the cosine rule are used to find angles and sides in triangles. What happens when one of the angles is obtuse? To deal with this we need to extend the definition of the basic trigonometric ratios from acute to obtuse angles. We use coordinate geometry to motivate the extended definitions as follows.
We draw the unit circle centre the origin in the Cartesian plane and mark the point on the circle in the first quadrant.
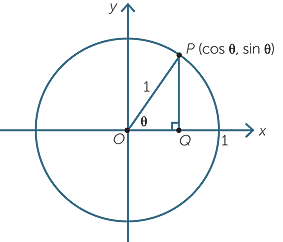 In the diagram shown, since
In the diagram shown, since 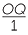 = cos θ, we can
= cos θ, we can
see that the x-coordinate of P is cos θ. Similarly,
the y-coordinate of P is sin θ.
Hence the coordinates of P are (cos θ, sin θ).
We can now turn this idea around and say that
if θ is the angle between OP and the positive x-axis, then:
- the cosine of θ is defined to be the x-coordinate of
the point P on the unit circle and - the sine of θ is defined to be the y-coordinate of the
point P on the unit circle.
This definition can be applied to all angles, both positive and negative, but in this module we will restrict the angle to be between 0° and 180°.
Consistency of the definitions
In the module, Introduction to Trigonometry, we defined sin θ =  and cos θ =
and cos θ =  , where 0° < θ < 90°. In the previous section we defined cos θ = OQ and sin θ = PQ. We must show that the two definitions agree.
, where 0° < θ < 90°. In the previous section we defined cos θ = OQ and sin θ = PQ. We must show that the two definitions agree.
The diagram below shows the right-angled triangle OAB, and the triangle OPQ both containing the angle θ. Triangle OPQ has its vertex P on the unit circle. These triangles are similar and so the ratio 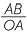 =
= 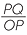 = PQ, which is the y-coordinate of the point P. Similarly
= PQ, which is the y-coordinate of the point P. Similarly 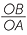 =
= 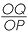 = 1, which is the x-coordinate of P.
= 1, which is the x-coordinate of P.

So we have shown the two definitions agree.
As an example, let us take θ to be 30°, so has coordinates (cos 30°, sin 30°).
Now move the point P around the circle to P′ so that OP′ makes an angle of 150° with the positive x-axis. Note that 30° and 150° are supplementary angles.
The coordinates of P′ are (cos 150°, sin 150°).
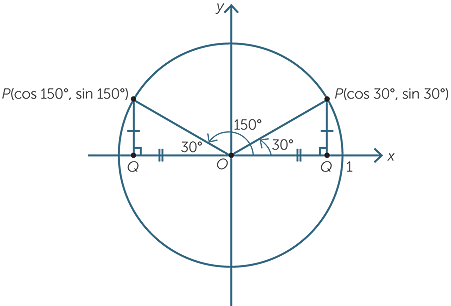
But we can see that the triangles OPQ and OP′Q′ are congruent, so the y-coordinates
of P and P′ are the same. Thus, sin 150° = sin 30°.
Also, the x-coordinates of P and P′ have the same magnitude but opposite sign,
so cos 150° = −cos 30°.
From this typical example, we see that if θ is any obtuse angle, then its supplement,
180°− θ is acute, and the sine of θ is given by
![]() sin θ = sin (180° − θ), where 90° < θ < 180°.
sin θ = sin (180° − θ), where 90° < θ < 180°.
Similarly, if θ is any obtuse angle then the cosine of θ is given by
![]() cos θ = −cos (180° − θ), where 90° < θ < 180°.
cos θ = −cos (180° − θ), where 90° < θ < 180°.
In words this says:
- the sine of an obtuse angle equals the sine of its supplement,
- the cosine of an obtuse angle equals minus the cosine of its supplement.
EXAMPLE
Find the exact value of:
a![]() sin 150°
sin 150°![]() b
b![]() cos 150°
cos 150° ![]() c
c![]() sin 120°
sin 120° ![]() d
d![]() cos 120°
cos 120°
Solution
| a | sin 150° | = sin (180 − 150)° | b | cos 150° | = −cos (180 − 150)° | |
| = sin 30° | = −cos 30° | |||||
= 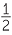 |
= −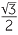 |
|||||
| c | sin 120° | = sin (180 − 120)° | d | cos 120° | = −cos (180 − 120)° | |
| = sin 60° | = −cos 60° | |||||
= 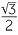 |
= −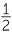 |
Note: You can verify these results using your calculator.
The sine rule is also valid for obtuse-angled triangles.
EXERCISE 4
 Reprove the sine rule
Reprove the sine rule  =
= 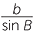 for a triangle in which angle A is obtus.
for a triangle in which angle A is obtus.
We can use the extended definition of the trigonometric functions to find the sine and cosine of the angles 0°, 90°, 180°.
EXERCISE 5
Draw a diagram showing the point on the unit circle at each of the above angles. Use the coordinates of to complete the entries in the table below.
| θ | 0° | 90° | 180° |
| sin θ | |||
| cos θ |
The tangent of an obtuse angle
For θ in the range 0° < θ < 90° or 90° < θ < 180° we define the tangent of an angle θ by
![]() tan θ =
tan θ = 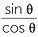 , for cos θ ≠ 0.
, for cos θ ≠ 0.
In the case when cos θ = 0, the tangent ratio is undefined. This will happen, when θ = 90°.
If θ is in the range 0° < θ < 90°, this definition agrees with the usual definition of
![]() tan θ =
tan θ = 
Hence, if θ is an obtuse angle, then
|
tan θ |
= |
(from the definition) |
|
|
= |
(since θ is obtuse) |
||
|
= −tan (180° − θ) |
(from the definition). |
Hence the tangent of an obtuse angle is the negative of the tangent of its supplement.
Note that tan 0° = 0 and tan 180°= 0 since the sine of these angles is 0 and that tan 90° is undefined since cos 90°= 0.
EXERCISE 6
Find the exact values of tan 150° and tan 120°.
In our work on congruence, it was emphasized that when applying the SAS congruence test, the angle in question had to be the angle included between the two sides. Thus, the following diagram shows two non-congruent triangles ABC and ABC′ with two pairs of matching sides sharing a common (non-included) angle.
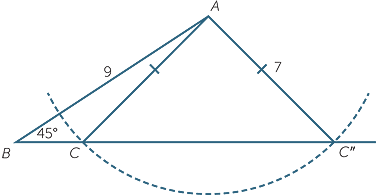
Suppose we are told that a triangle PQR has PQ = 9,  PQR = 45°, and PR = 7. Then the angle opposite PQ is not uniquely determined. There are two non-congruent triangles that satisfy the given data.
PQR = 45°, and PR = 7. Then the angle opposite PQ is not uniquely determined. There are two non-congruent triangles that satisfy the given data.
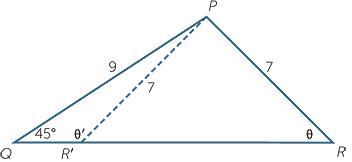
Applying the sine rule to triangle we have
![]()
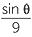 =
= 
and so sin θ = 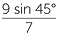 ≈ 0.9091.
≈ 0.9091.
Thus θ ≈ 65°, assuming that θ is acute. But the supplementary angle θ′ = 115°. The angle PR′Q also satisfies the given data. This situation is sometimes referred to as the ambiguous case.
Since the angle sum of a triangle is 180°, in some circumstances only one of the two angles calculated is geometrically valid.
EXERCISE 7
 Find the value of θ in the following diagram,
Find the value of θ in the following diagram,
explaining why the answer is unique.
We know from the SAS congruence test, that a triangle is completely determined if we are given two sides and the included angle. However, if we know two sides and the included angle in a triangle, the sine rule does not help us determine the remaining side.
The second important formula for general triangles is the cosine rule.
Suppose ABC is a triangle and that the angles A and C are acute. Drop a perpendicular from B to AC and mark the lengths as shown in the diagram.
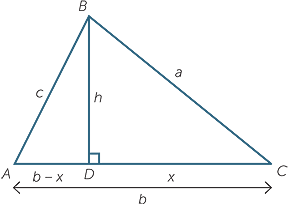
In  BDA, Pythagoras’ theorem gives
BDA, Pythagoras’ theorem gives
![]() c2 = h2 + (b − x)2.
c2 = h2 + (b − x)2.
Also in  CBD, another application of Pythagoras’ theorem gives
CBD, another application of Pythagoras’ theorem gives
![]() h2 = a2 − x2.
h2 = a2 − x2.
Substituting this expression for into the first equation and expanding,
| c2 | = a2 − x2 + (b − x)2 | |
| = a2 − x2 + b2 − 2bx + x2 | ||
| = a2 + b2 − 2bx. |
Finally, from  CBD, we have x = a cos C and so
CBD, we have x = a cos C and so
c2 = a2 + b2 − 2abcos C
This last formula is known as the cosine rule. By relabeling the sides and angle, we can also write a2 = b2 + c2 − 2bc cos A, and b2 = a2 + c2 − 2ac cos B.
Notice that if C = 90° then, since cos C = 0, we obtain Pythagoras’ theorem, and so we can regard the cosine rule as Pythagoras’ theorem with a correction term.
The cosine rule is also true when C is obtuse, but note that in this case the final term in the formula will produce a positive number, because the cosine of an obtuse angle is negative. Some care must be taken in this instance.
EXAMPLE
Find the value of x to one decimal place.
solution
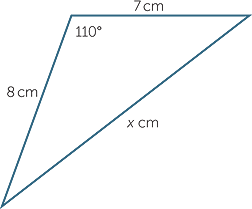 Applying the cosine rule:
Applying the cosine rule:
|
x2 |
= 72 + 82 − 2 × 7 × 8 cos 110° |
|
|
= 151.30... |
||
|
so |
x |
= 12.3 (to one decimal place) |
EXERCISE 8
Prove that the cosine rule also holds in the case when C is obtuse.
We know from the SSS congruence test that if the three sides of a triangle are known then the three angles are uniquely determined. Again, the sine rule is of no help in finding them since it requires the knowledge of (at least) one angle, but we can use the cosine rule instead.
We can substitute the three side lengths a, b and c into the formula c2 = a2 + b2 − 2ab cos C where C is the angle opposite the side c, and then re-arrange to find cos C and hence C.
Alternatively, we can re-arrange the formula to obtain
![]() cos C =
cos C = 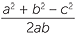
and then substitute. Students may care to rearrange the cosine rule or learn a further formula. Using this form of the cosine rule often reduces arithmetical errors.
Recall that in any triangle ABC, if a > b then  A >
A >  B.
B.
EXAMPLE
A triangle has side lengths 6 cm, 8 cm and 11 cm. Find the smallest angle in the triangle.
Solution
 The smallest angle in the triangle is opposite the smallest side.
The smallest angle in the triangle is opposite the smallest side.
Applying the cosine rule:
| 62 | = 82 + 112 − 2 × 8 × 11 × cos θ | |
| cos θ | = 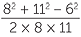 |
|
= 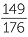 |
||
| and so | θ | ≈ 32.2 |
Extension — The longest side and the largest angle of a triangle
In the module Congruence, we proved an important relationship between the relative sizes of the angles of a triangle and the relative lengths of its sides: The angle of a triangle opposite a longer side is larger than the angle opposite a shorter side.
For scalene triangles, this can be restated in terms of inequalities of all three sides as follows:
If  ABC is a triangle in which a > b > c, then A > B > C.
ABC is a triangle in which a > b > c, then A > B > C.
This result can be proved in an interesting way using either the sine rule or the cosine rule.
The longest side and the sine rule
The following exercise uses the fact that sin θ increases from 0 to 1 as θ increases from
0° to 90°.
EXERCISE 9
Let  ABC be a triangle in which a > b > c.
ABC be a triangle in which a > b > c.
- What can you conclude about the relative sizes of sin A, sin B and sin C using the sine rule?
- If no angle is obtuse, what can you conclude about the relative sizes of A, B and C?
- If a triangle PQR has an obtuse angle
 P = 180° − θ, where θ is acute, use the identity sin (180°− θ) = sin θ to explain why sin P is larger than sin Q and sin R.
P = 180° − θ, where θ is acute, use the identity sin (180°− θ) = sin θ to explain why sin P is larger than sin Q and sin R.
- Hence prove that if the triangle ABC has an obtuse angle, then A > B > C.
The longest side and the cosine rule
This exercise uses the fact that cos θ decreases from 1 to −1 as θ increases from 0° to 180°.
EXERCISE 10
Let  ABC be a triangle in which a > b > c.
ABC be a triangle in which a > b > c.
- a
- Write down cos A and cos B in terms of a, b and c, and express each in terms of their common denominator 2abc.
- b
- Show that cos B − cos A =
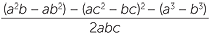
 =
= 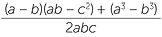 .
.
- c
- Hence explain why cos B > cos A.
- d
- Similarly explain why cos C > cos B, and hence show that A > B > C.
EXERCISE 11
- a
- Use Pythagoras’ theorem to show that the hypotenuse is the longest side of a right-angled triangle
- b
- Why is the result of part a special case of the theorem above?
We saw in the module, Introductory Trigonometry that if we take any triangle with two given sides and about a given (acute) angle θ, then the area of the triangle is given by
![]() Area =
Area = 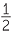 ab sin θ.
ab sin θ.
EXERCISE 12
Derive this formula in the case when θ is obtuse.
EXERCISE 13
A triangle has two sides of length 5 cm and 4 cm containing an angle θ. Its area is 5 cm2. Find the two possible (exact) values of θ and draw the two triangles that satisfy the
given information.
EXERCISE 14
Write down two expressions for the area of triangle and derive the sine rule from them.
The sine and cosine rules can be used to solve a range of practical problems in surveying and navigation.
EXAMPLE
The point M is directly across the river from the base B of a tree AB. From a point 7 metres upstream from M, the angle of elevation of the top A of the tree is 17°. From a point Q, 5 metres downstream from M the angle of elevation of the top of the tree is 19°. Assuming that PMQ is a straight line and that the tree is on the edge of the river,
we wish to find the width w metres of the river.
Solution
In problems such as these, it is imperative to draw a careful diagram.
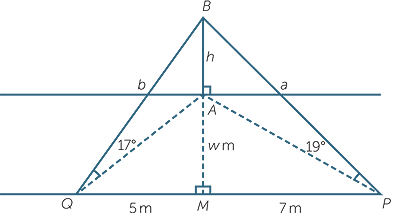
Let BP = a, BQ = b, and AB = h, and then applying Pythagoras’ theorem to triangles
BMP and BMQ, we have a =  , b =
, b =  .
.
From triangles ABP and ABQ we have h = a sin 17°, h = b sin 19°.
Equating these, substituting in the values of a and b and squaring we arrive at
(49 + w2)sin2 17° = (25 + w2)sin2 19°
We can now make w2 the subject and obtain w2 = 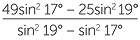 , and so
, and so
w ≈ 8.66 m correct to 2 decimal places.
Note: Do not evaluate until the last step to retain full calculator accuracy.
Civil engineers analyzing forces and stresses in buildings and other structures often use vectors to represent the direction and magnitude of these forces. A vector is an arrow which has both direction and magnitude. The sine and cosine rules are used in vector diagrams to find resultant forces and stresses. This is an important application.
As well as having practical uses, the sine and cosine rules can be used to derive theoretical results, known as trigonometric identities that have important implications and applications in later work. Among these are the double angle results which we will describe below.
Using the area formula, A =  ab sin C, for a triangle with two sides a and b, containing an angle C, we can do the following:
ab sin C, for a triangle with two sides a and b, containing an angle C, we can do the following:
Fix acute angles a and β and let angle C = a + β. From the point C draw CD of length y and construct triangle ABC as shown in the diagram, where BA is perpendicular to CD.
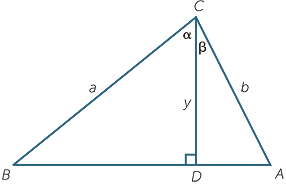 From the diagram, we have
From the diagram, we have
 = cos α => y = a cos α = cos α => y = a cos α |
(1) | |||
| and | 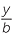 = cos β => y = b cos β = cos β => y = b cos β |
(2). |
Comparing areas,
![]()
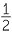 ab sin (α + β) =
ab sin (α + β) = 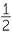 ay sin α +
ay sin α + 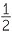 by sin β.
by sin β.
Substituting in the value of y from (2) into the first term and that from (1) into the second, we have, after some simplification,
sin (α + β) = sin α cos β + cos α sin β.
In the discussion above we assumed that α, β were acute angles. This identity holds for all
α and β but to show this requires a different approach.
Note that sin (α + β) ≠ sin α + sin β. For example, sin(60°+30°) = sin 90° = 1, whereas
sin 60° + sin 30° = 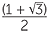 ≠ 1.
≠ 1.
EXERCISE 15
Use the above formula to show that the exact value of sin 75° is 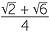 .
.
Putting α = β = θ in the above formula, we obtain the double angle formula
for sine, namely
![]() sin 2θ = 2sin θ cos θ.
sin 2θ = 2sin θ cos θ.
There is a similar double angle formula for cosine,
![]() cos 2θ = cos2 θ − sin2 θ.
cos 2θ = cos2 θ − sin2 θ.
Both formulas are extremely useful when calculus is applied to the trigonometric functions.
Angles of any magnitude and the trigonometric functions
We saw in this module how to use the unit circle to give meaning to the sine and cosine of an obtuse angle. This definition can be extended to include angles greater than 180° and also to negative angles.
Thus, for example, if θ is between 180° and 270°, then sin θ = −sin (θ − 180°) and
cos θ = −cos (θ − 180°).
Once we can find the values of sin θ and cos θ for values of θ, we can plot graphs of the functions y = sin θ, y = cos θ.
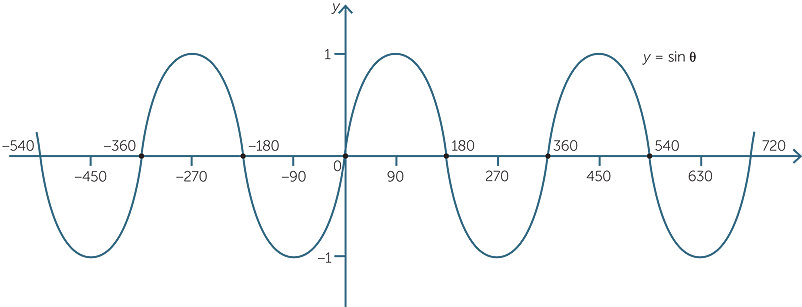
These ideas will be developed in the module, Trigonometric Functions.
The graphs of the sine and cosine functions are used to model wave motion and electrical signals. They are an essential part of modern signal processing and telecommunications. This provides a breathtaking example of how a simple idea involving geometry and ratio was abstracted and developed into a remarkably powerful tool that has changed the world.
In the module, Introductory Trigonometry, we mentioned that the Greeks had a version of trigonometry involving chords. This is shown in the diagram below.
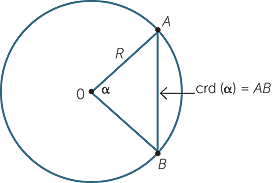
In the diagram, the chord of the angle is the length of the chord that subtends an angle α at the centre in the circle of radius R.
Ptolemy (85-185AD), who lived and worked in Alexandria, wrote an extremely influential book called the Mathematical Syntaxis. It was translated into Arabic and given the Arabic title of Almagest.
Ptolemy considered chords subtending an angle α on the circumference. Using modern notation, if we take a diameter of AB length 1 unit as shown and a chord AC subtending an angle α at the circumference, then the lengths AC and BC are respectively sin α and cos α.
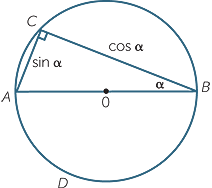
Since angles on the circumference subtended by the same arc are equal, if α is the angle subtended by any chord in this circle, then the length of that chord is always sin α.
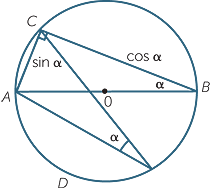
Ptolemy also showed that if ABCD is a cyclic quadrilateral, then
![]()
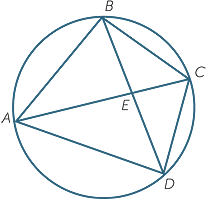
![]() AB.CD + BC.DA = AC.BD.
AB.CD + BC.DA = AC.BD.
That is, the sum of the products of the opposite sides of a cyclic quadrilateral is equal to the product of the diagonals.
This result is known as Ptolemy’s theorem.
Applying Ptolemy’s theorem in the diagram below, where the circle has diameter 1, we obtain the result sin (α + β) = sin α cos β + cos α sin β, that we derived above.

Using this, and other formulas, Ptolemy was able to construct a detailed table of chords of angles. Since chords are closely related to the sine ratio, he essentially had a table of sines.
Given a triangle ABC, we can draw its circumcircle with diameter BD as shown. Let 2R be the diameter of the circumcircle.
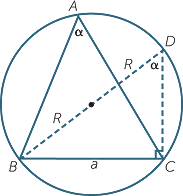
Then for α acute, the sine of angle BDC is given by
![]() sin
sin  BDC = sin α =
BDC = sin α = 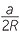 .
.
Re-arranging gives  = 2R.
= 2R.
Thus the quantities  ,
, 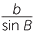 and
and  in the sine rule are all equal to the diameter of the circumcircle of the triangle ABC.
in the sine rule are all equal to the diameter of the circumcircle of the triangle ABC.
Regiomontanus (1436-1476), who wrote the first modern European book on trigonometry, included the sine rule and its derivation in his work.
The regular pentagram and regular pentagon
The regular pentagram and the regular pentagon have always been a source of fascination and is often used in astrology. It is based on a triangle whose properties are investigated in the following exercise.
EXERCISE 16
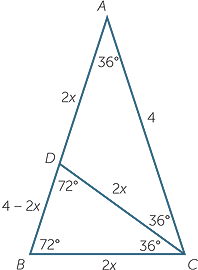
We begin with an isosceles triangle with angles 72°, 72°, 36°, as shown. This triangle
occurs naturally inside both the regular pentagon and the regular pentagram.
For ease of calculation we take the two equal sides to be 4 units in length.
We take the point D on AB such that  BDC = 72°. Finally, we let BC = 2x.
BDC = 72°. Finally, we let BC = 2x.
a Show that the information marked on the diagram is correct.
b Prove that the triangles ABC and CDB are similar.
c Deduce that 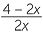 =
= 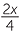 and solve this equation to obtain x =
and solve this equation to obtain x = ![]() − 1.
− 1.
d By dropping a perpendicular from A to BC show that cos 72° = 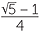 .
.
e Use the identity cos2 θ + sin2 θ = 1 to show that sin 72° = 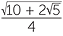 .
.
Exercise 1
a −1 b 50(![]() + 1)
+ 1)
Exercise 2
tan-1 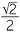 ≈ 35.26°, correct to two decimal places.
≈ 35.26°, correct to two decimal places.
Exercise 3
AP = 24.57… m and OA = 11.54 m to the nearest cm.
Exercise 4
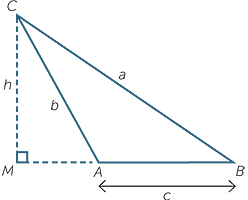 Let
Let  CAM = θ
CAM = θ
Therefore  CAB = 180° − θ
CAB = 180° − θ
h = b sin θ (triangle CAM) and h = a sin B (triangle CAB)
| Therefore | a sin B = b sinθ | = b sin (180° − A) |
| = b sin A | ||
so  |
= 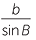 |
hence the result.
Exercise 5
sin 0° = 0, sin 90° = 1, sin 180° = 0
cos 0° = 1, cos 90° = 0, cos 180° = −1
Exercise 6
−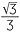 , −
, −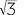
Exercise 7
sin−1 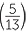 ≈ 22.62° (correct to two decimal places). The two sides and the right angle define a unique triangle (RHS congruence).
≈ 22.62° (correct to two decimal places). The two sides and the right angle define a unique triangle (RHS congruence).
Exercise 8
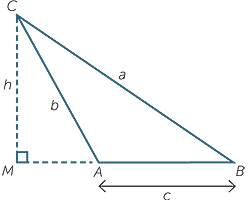 In triangle BCM, h2 = a2 − (c + MA)2
In triangle BCM, h2 = a2 − (c + MA)2
In triangle CMA, h2 = b2 − MA2
Therefore, a2 − (c + MA)2= b2 − MA2
a2 = b2 + c2 + 2c × MA
But MA = b cos (180° − A) = − b cos A
Hence a2 = b2 + c2 − 2bc cos A
Exercise 9
a sin A > sin B > sin C (if a > b and a sin B = b sin A then sin A > sin B
b By the remark at the beginning of this paragraph, A > B > C.
c The angles P and Q add to θ, because the angle sum of the triangle is 180°.
Hence P and Q are smaller than θ, so sin P and sin Q are less than sin θ = sin P.
d From part c, the obtuse angle is A, which is therefore the largest of the three angles.
Hence sin B > sin C, where B and C are acute, so A > B > C.
Exercise 10
| a | cos A | =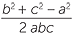 |
and | cos B | = 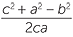 |
||
= 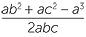 |
|
| b | Grouping terms, | |
| cos B − cos A | =  |
|
= 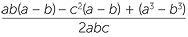 |
||
= 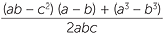 |
c From a > b > c > 0, it follows that ab > c2 and a3 > b3. Hence cos B > cos A.
d A similar argument proves that cos C > cos B, so cos C > cos B > cos A.
By the remark at the start of this paragraph, A > B > C.
Exercise 11
a Let  ABC be right-angled at C. Then AB2 = AC2 + BC2. Hence AB2 is larger than both AC2 and BC2, so AB is longer than both AC and BC.
ABC be right-angled at C. Then AB2 = AC2 + BC2. Hence AB2 is larger than both AC2 and BC2, so AB is longer than both AC and BC.
b In a right-handed triangle, the other two angles are acute, because the angle sum of the triangle is 180°. Hence the right angle is the largest angle.
Exercise 12
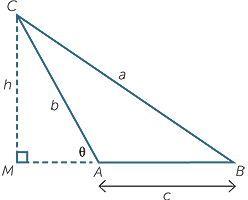 We use the same diagram as that used for the obtuse angle case proof of the sine and cosine rule.
We use the same diagram as that used for the obtuse angle case proof of the sine and cosine rule.
| Area | =  c × h = c × h = 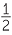 cb sin θ cb sin θ |
= 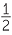 cb sin A cb sin A |
The stated result is obtained by symmetry of argument.
Exercise 13
θ = 30° or 150°
Exercise 14
For a given triangle ABC, 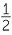 cb sin A =
cb sin A = 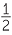 ca sin B. Therefore bsin A = asin B and
ca sin B. Therefore bsin A = asin B and  =
= 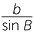 .
.
Exercise 15
| sin 75° | = sin (45° + 30°) = sin 45° cos 30° + sin 30° cos 45° |
= 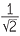 × × 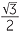 + + 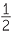 × ×  |
|
= 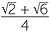 |
Exercise 16
| a |  DCB = 36° (angle sum of triangle), DCB = 36° (angle sum of triangle),  ACD = 36° ( ACD = 36° ( DCA = 36° and DCA = 36° and  ACD = 72°) ACD = 72°) |
|
| CD = 2x (triangle CBD is isosceles), DA = 2x (triangle CDA is isosceles), | ||
| DB = AB − AD = 4 − 2x. |
b![]() Triangle ABC is similar to triangle CDB (AA)
Triangle ABC is similar to triangle CDB (AA)
c![]()
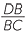 =
= 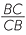
![]() d cos B =
d cos B = 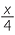
![]() e sin2 B = 1 −
e sin2 B = 1 −  =
= 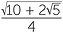
| hence | 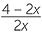 |
= 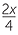 |
||
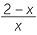 |
= 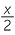 |
|||
| x2 − 2x | = 4 | |||
| x2 + 2x + 1 | = 5 | |||
| (x + 1)2 | = 5 | |||
| x | = −1 + |
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()