The Improving Mathematics Education in Schools (TIMES) Project

return to index

Multiplication and Division

Number and Algebra : Module 3Year : F-4

June 2011

PDF Version of module

Assumed Knowledge

Much of the building of understanding of early mathematics occurs concurrently, so a child can be developing the basic ideas related to multiplication and division whilst also investigating the place-value system. However, there are some useful foundations necessary for multiplication and division of whole numbers:

• Some experience with forwards and backwards skip-counting.
• Some experience doubling and halving small numbers.

(see F-4 Module Counting and Place Value and F-4 Module Addition and Subtraction)

Motivation

One way of thinking of multiplication is as repeated addition. Multiplicative situations arise when finding a total of a number of collections or measurements of equal size. Arrays are a good way to illustrate this. Some division problems arise when we try to break up a quantity into groups of equal size and when we try to undo multiplications.

Multiplication answers questions such as:

1

Judy brought 3 boxes of chocolates. Each box contained 6 chocolates. How many chocolates did Judy have?

2

Henry has 3 rolls of wire. Each roll is 4m long. What is the total length of wire that Henry has?

Division answers questions such as:

1

How many apples will each friend get if four friends share 12 apples equally
between them?

2

If twenty pens are shared between seven children how many does each child receive, and how many are left over?

Addition is a useful strategy for calculating ‘how many’ when two or more collections of objects are combined. When there are many collections of the same size, addition is not the most efficient means of calculating the total number of objects. For example, it is much quicker to calculate 6 × 27 by multiplication than by repeated addition.

Fluency with multiplication reduces the cognitive load in learning later topics such as division. The natural geometric model of multiplication as rectangular area leads to applications in measurement. As such, multiplication provides an early link between arithmetic and geometry.

Fluency with division is essential in many later topics and division is central to the calculations of ratios, proportions, percentages and slopes. Division with remainder is a fundamental idea in electronic security and cryptography.

Content

Multiplication and division are related arithmetic operations and arise out of everyday experiences. For example, if every member of a family of 7 people eats 5 biscuits, we can calculate 7 × 5 to work out how many biscuits are eaten altogether or we can count by ‘fives’, counting one group of five for each person. In many situations children will use their hands for multiples of five.

For whole numbers, multiplication is equivalent to repeated addition and is often introduced using repeated addition activities. It is important, though that children see multiplication as much more than repeated addition.

If we had 35 biscuits and wanted to share them equally amongst the family of 7, we would use sharing to distribute the biscuits equally into 7 groups.

We can write down statements showing these situations:

7 × 5 = 35 and 5 × 7 = 35

Also,

35 ÷ 5 = 7 and 35 ÷ 7 = 5

Introducing vocabulary and symbols

There is a great deal of vocabulary related to the concepts of multiplication and division. For example,

multiplication − multiply, times, product, lots of, groups of, repeated addition

division − sharing, divided by, repeated subtraction

Some of these words are used imprecisely outside of mathematics. For example, we might say that a child is the product of her environment or we insist that children ‘share’ their toys even though we do not always expect them to share equally with everyone.

It is important that children are exposed to a variety of different terms that apply in multiplication and division situations and that the terms are used accurately. Often it is desirable to emphasise one term more than others when introducing concepts, however a flexibility with terminology is to be aimed for.

Looking at where words come from gives us some indication of what they mean. The word ‘multiply’ was used in the mathematical sense from the late fourteenth century and comes from the Latin multi meaning ‘many’ and plicare meaning ‘folds’ giving multiplicare - ‘having many folds’, which means ‘many times greater in number’. The term ‘manyfold’ in English is antiquated but we still use particular instances such as ‘twofold’ or threefold’.

The word ‘divide’ was used in mathematics from the early 15th century. It comes from the Latin, dividere meaning ‘to force apart, cleave or distribute’. Interestingly, the word widow has the same etymological root, which can be understood in the sense that a widow is a woman forced apart from her husband.

Use of the word ‘product’

The product of two numbers is the result when they are multiplied. So the product of
3 and 4 is the multiplication 3 × 4 and is equal to 12.

It is important that we use the vocabulary related to multiplication and division correctly. Many years ago we were told to ‘do our sums’ and this could apply to any calculation using any of the operations. This is an inaccurate use of the word ‘sum’. Finding the ‘sum’ of two or more numbers means to add them together. Teachers should take care not to use the word ‘sum’ for anything but addition.

The symbols × and ÷

The × symbol for multiplication has been in use since 1631. It was chosen for religious reasons to represent the cross. We read the statement 3 × 4 as ‘3 multiplied by 4’.

In some countries a middle dot is used so 3 × 4 is written as 3.4. In algebra it is common to not use a symbol for multiplication at all. So, a × b is written as ab.

The division symbol ÷ is known as the obelus. It was first used to signify division in 1659. We read the statement 12 ÷ 3 as ‘12 divided by 3’. Another way to write division in school arithmetic is to use the notation , meaning ‘12 divided by 3’, but sometimes read as
‘3 goes into 12’.

Mathematicians almost never use the ÷ symbol for division. Instead they use fraction notation. The writing of a fraction is really another way to write division. So 12 ÷ 4 is equivalent to writing 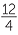, where the numerator, 12, is the dividend and the denominator, 4, is the divisor. The line is called called a vinculum, which is a Latin word meaning ‘bond or link’.

Once students are becoming fluent with the concepts of multiplication and division then the symbolic notation, × for multiplication and ÷ for division, can be introduced. Initially, the ideas will be explored through a conversation, then written in words, followed by a combination of words and numerals and finally using numerals and symbols. At each step, when the child is ready, the use of symbols can reflect the child’s ability to deal with abstract concepts.

MODELLING MULTIPLICATION

Modelling multiplication by arrays

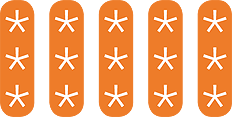
Rectangular arrays can be used to model multiplication. For example, 3 × 5 is illustrated by

We call 15 the product of 3 and 5, and we call 3 and 5 factors of 15.

By looking at the rows of the array we see that

3 × 5 = 5 + 5 + 5

By looking at the columns of the array we also see that

5 × 3 = 3 + 3 + 3 + 3 + 3

This illustrates 3 × 5 = 5 × 3. We say that multiplication is commutative.

Arrays are useful because they can be used with very small as well as very large numbers, and also with fractions and decimals.

Modelling multiplication by skip-counting and on the number line

Skip-counting, such as reciting 3, 6, 9, 15,..., is one of the earliest introductions to repeated addition and hence to multiplication. This can be illustrated on a number line as shown for 3 × 5 = 15 below.

3 × 5 = 15

On the number line, the fact that 3 + 3 + 3 + 3 + 3 = 5 + 5 + 5 is not so obvious; the previous image shows 5 + 5 + 5, whereas 3 + 3 + 3 + 3 + 3 looks quite different.

Skip-counting is important because it helps children learn their multiplication tables.

Modelling multiplication by area

Replacing objects in an array by unit squares provides a natural transition to the area model of multiplication. This is illustrated below for 3 × 5.

At this stage, we are simply using unit squares instead of counters or stars. We can also use the area model of multiplication later for multiplication of fractions.

Properties of Multiplication

One of the advantages of the array and area approach is that properties of multiplication are more apparent.

Commutativity

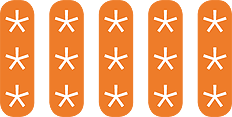
As discussed above, turning the 3 × 5 array on its side illustrates that 3 × 5 = 5 × 3 because the total number of objects in the array does not change.

3 × 5 = 5 × 3

We saw this before by looking at the rows and columns separately, but we can also do this by turning the rectangle on its side. The area of the rectangle does not change.

3 × 5 = 5 × 3

Associativity

Another important property of multiplication is associativity, which says that

a × (b × c) = (a × b) × c for all numbers.

We can demonstrate this with the numbers 2, 3 and 4:

2 × (3 × 4) = (2 × 3) × 4

Associativity of multiplication ensures that the expression a × b × c is unambiguous.

Any-order property

We usually don’t teach young children associativity of multiplication explicitly when introducing multiplication. Instead, we teach the any-order property of multiplication, which is a consequence of the commutative and associative properties.

The any-order property of multiplication is analogous to the any- order property of addition. Both associativity and commutativity are nontrivial observations; note that subtraction and division are neither commutative nor associative. Once we are familiar with the arithmetic operations we tend to take both associativity and commutativity of multiplication for granted, just as we do for addition. Every so often, it is worth reflecting that commutativity and associativity combine to give the important and powerful any-order properties for addition and multiplication.

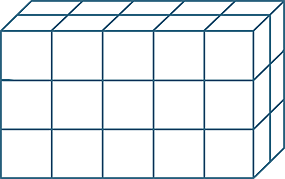
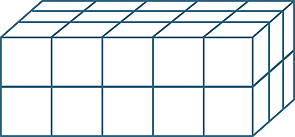
Multiplying three whole numbers corresponds geometrically to calculating the number of unit cubes in (or volume of) a rectangular prism. The any-order property of multiplication means that we can calculate this volume by multiplying the lengths of the sides in any order. The order of the calculation corresponds to slicing the volume up in different ways.

5 × 2 = 2 × 5		(5 × 2) × 3 = (2 × 5) × 3
3 × 2 = 2 × 3		(3 × 2) × 5 = (2 × 3) × 5
5 × 3 = 3 × 5		(5 × 3) × 2 = (3 × 5) × 2

We can apply this to the multiplication of three or more numbers, it doesn’t matter in which order we do this.

Distributivity of Multiplication over Addition

The equation 3 × (2 + 4) = (3 × 2) + (3 × 4) is an example of the distributivity of multiplication over addition. With arrays, this corresponds to the following diagram.

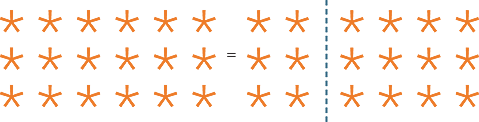
With areas it corresponds to the diagram below.

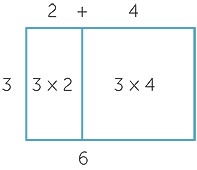
Multiplication is also distributive over subtraction.

For example 7 × (10 − 2) = 7 × 10 − 7 × 2.

We use the distributive property to enable us to reduce multiplication problems to a combination of familiar multiples. For example,

7 × 101 = 7 × (100 + 1) = 700 + 7 = 707,

7 × 99 = 7 × (100 − 1) = 700 − 7 = 693,

7 × 102 = 7 × (100 + 2) = 700 + 14 = 714,

and

7 × 98 = 7 × (100 − 2) = 700 − 14 = 686.

The effect of multiplying by one

When any number is multiplied by 1, the number is unchanged. For example,

5 × 1 = 5 = 1 × 5

We call 1 the multiplicative identity. It is important to have this conversation with young children in very simple terms, using lots of examples in the early stages of developing understanding about multiplication.

Zero is the identity element for addition. When nothing is added to a set there is no effect on the number of objects in that set. For example,

5 + 0 = 5 = 0 + 5.

This is true for all addition. Hence, we call zero the identity element for addition of
whole numbers.

The effect of multiplying by zero

When any number is multiplied by zero the result is zero. Situations showing the effect of multiplying by zero can be acted out with children using concrete objects.

For example,

If I have 5 baskets with three apples in each I have 5 × 3 = 15 apples in total.
However, if I have 5 baskets with 0 apples in each, the result is 5 × 0 = 0 apples in total.

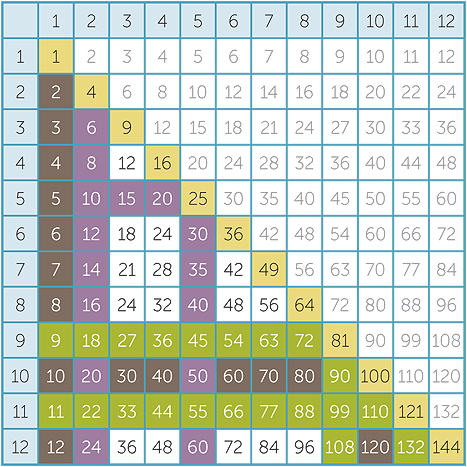
Learning the multiplication table.

Fluency with multiplication tables is essential for further mathematics and in everyday life. For a while it was considered unnecessary to learn multiplications tables by memory, but it is a great help to be fluent with tables in many areas of mathematics.

If students can add a single-digit number to a two-digit number, they can at least reconstruct their tables even if they have not yet developed fluency. It is therefore essential to ensure that students can add fluently before they begin to learn their ‘tables’.

We strongly recommend that students learn their multiplication facts up to 12 × 12. This is primarily because the 12 times table is essential for time calculations — there are 12 months in a year, 24 hours in a day, and 60 minutes in an hour. Familiarity with dozens is useful in everyday life because packaging in 3 × 4 arrays is so much more convenient than in 2 × 5 arrays. In addition, the 12 × 12 table has many patterns that can be constructively exploited in pre-algebra exercises.

A straightforward approach to learning the tables is to recite each row, either by heart or by skip-counting. However, students also need to be able to recall individual facts without resorting to the entire table.

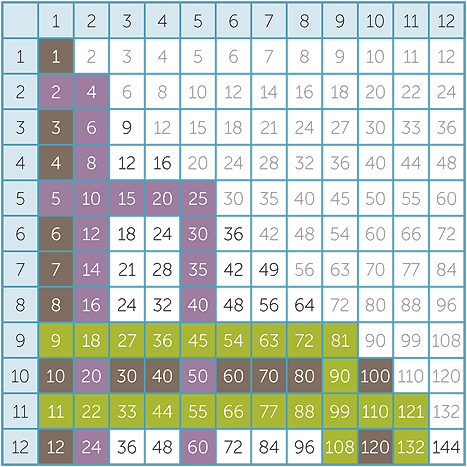
Looking at the 12 × 12 multiplication table gives the impression that there are 144 facts to be learnt.

However, there are several techniques that can be used to reduce the number of facts to be learnt.

• The commutativity of multiplication (8 × 3 = 3 × 8) immediately reduces this number to 78.
• The 1 and 10 times tables are straightforward and their mastery reduces the number of facts to be learnt to 55.

• The 2 and 5 times tables are the easiest to learn and their mastery further reduces the number of facts to be learnt to 36.

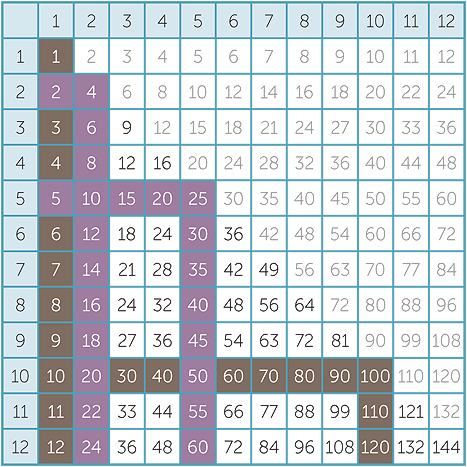
• The 9 and 11 times tables are the next easiest to skip-count because 9 and 11 differ from 10 by 1. This reduces the number of facts to 21. Children may notice the decreasing ones digit and increasing tens digit in the nine times table. They may also be intrigued by the fact that the sum of the digits of a multiple of 9 is always 9.

• The squares are useful and can be learnt just as one might learn a times table.

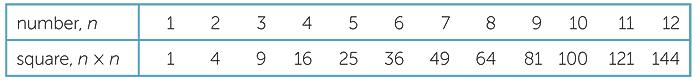
This reduces the number of terms to be learnt to 15.

Whatever techniques are used, the aim should be fluency.

MODELLING DIVISION

Division always involves splitting something into a number of equal parts, but there are many contrasting situations that can all be described by ‘division’. Before introducing the standard algorithm for division, it is worthwhile discussing some of these situations under the headings:

• Division without remainder,
• Division with remainder.

Division without remainder

Here is a simple model of the division 24 ÷ 8.

Question: If I pack 24 apples into boxes, each with 8 apples, how many boxes will there be?

We can visualise the packing process by laying out the 24 apples successively in rows of 8, as in the diagrams below.

The 3 rows in the last array use up all 24 apples, so there will be 3 full boxes, with no apples left over. The result is written in mathematical symbols as

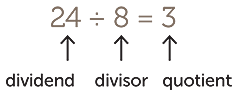
The number 24 is called the dividend (‘that which is to be divided’). The number 8 is called the divisor (‘that which divides’). The number 3 is called the quotient, (from the Latin quotiens meaning ‘how many times’).

Modelling division by skip-counting and on the number line

Division without remainder can be visualized as skip-counting.

0, 8, 16, 24…

On the number line we count in 8s until we reach 24.

Using arrays to show division without remainder is the inverse of multiplication

The rectangular array that we produced when we modeled 24 ÷ 8 is exactly the same array that we would draw for the multiplication 3 × 8 = 24.

In our example:

• The statement 24 = 8 × 3 means ‘three boxes, each with 8 apples, is 24 apples’, and
• The statement 24 ÷ 8 = 3 means ‘24 apples make up 3 boxes, each with 8 apples’.

Division without remainder is the inverse process of multiplication.

The multiplication statement 24 = 8 × 3 can in turn be reversed to give a second division statement

24 ÷ 3 = 8

which answers the question, ‘What is 24 divided by 3?

This corresponds to rotating the array by 90°, and regarding it as made up of 8 rows of 3. It answers the question, ‘If I pack 24 apples into boxes each holding 3 apples, how many boxes will be required?’

So the division statement 24 ÷ 8 = 3 now has four equivalent forms:

24 ÷ 8 = 3 and 24 = 8 × 3 and 24 = 3 × 8 and 24 ÷ 3 = 8.

Two models of division without remainder

This section is included for teachers because
children’s questions often concern pairs of
situations similar to those described here.

If we have 24 balloons to share equally, there
are two ways we can share them.

The first way is by asking ‘How many groups?’

For example, if we have 24 balloons and we give
8 balloons each to a number of children, how many
children get 8 balloons?

If we split 24 balloons into groups of 8, then 3 children get 8 balloons each.

We say ‘24 divided by 8 is 3’. This is written as 24 ÷ 8 = 3.

We can see this from the array:

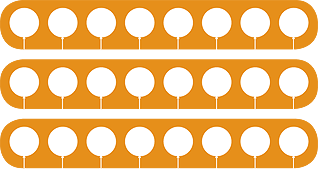
3 lots of 8 make 24 24 ÷ 8 = 3

The second way is by asking ‘How many in each group?’ For example, if we share
24 balloons among 8 children, how many balloons does each child receive? We want
to make 8 equal groups. We do this by handing out one balloon to each child. This uses
8 balloons. Then we do the same again.

We can do this 3 times, so each child gets 3 balloons.

Again, we can see this from the multiplication array:

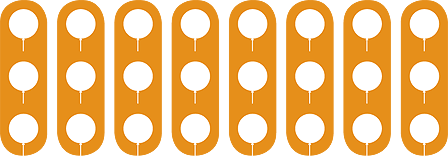
So dividing 24 by 8 is the same as asking ‘Which number do I multiply 8 by to get 24?’

For each division problem, there is usually an associated problem modelling the same division statement. The ‘balloons’ example above shows how two problems can have the same division statement. One problem with balloons is the associate of the other.

Division with remainder

We will now use apples to model 29 ÷ 8.

Question: If I pack 29 apples into boxes, each with 8 apples, how many boxes will there be?

As before, we can visualise the packing process by laying out the 29 apples successively in rows of 8:

We can lay out 3 full rows, but the last row only has five apples, so there will be 3 full boxes and 5 apples left over. The result is written as

dividend divisor quotient remainder

The number 5 is called the remainder because there are 5 apples left over. The remainder is always a whole number less than the divisor.

As with division without remainder, skip-counting is the basis of this process:

0, 8, 16, 24, 32,…

We locate 29 between successive multiples 24 = 8 × 3 and 32 = 8 × 4 of the divisor 8. Then we subtract to find the remainder 29 − 24 = 5.

We could also have answered the question above by saying, ‘There will be four boxes, but the last box will be 3 apples short.’

This corresponds to counting backwards from 32 rather than forwards from 24, and the corresponding mathematical statement would be

29 ÷ 8 = 4 remainder (−3).

It is not normal practice at school, however, to use negative remainders. Even when the question demands the interpretation corresponding to it, we will always maintain the usual school convention that the remainder is a whole number less than the divisor. Division without remainder can be regarded as division with remainder 0. During the location process, we actually land exactly on a multiple instead of landing between two of them. For example, 24 ÷ 8 = 3 remainder 0, or more simply, 24÷ 8 = 3, and we say that

24 is divisible by 8 and that 8 is a divisor of 24.

The corresponding multiplication and addition statement

The 29 apples in our example were packed into 3 full boxes of 8 apples, with 5 left over. We can write this as a division, but we can also write it using a product and a sum,

29 ÷ 8 = 3 remainder 5 or 29 = 8 × 3 + 5

So for division with remainder there is a corresponding statement with a multiplication followed by an addition, which is more complicated than division without remainder.

Two models of division with remainder

As before, problems involving division with remainder usually have an associated problem modelling the same division statement. Continuing with our example of

29 ÷ 8 = 3 remainder 5:

Question: How many bags of 8 apples can I make from 29 apples and how many are left over?

Question: I have 29 apples and 8 boxes. How many apples should I put in each box so that there is an equal number of apples in each box and how many are leftover?

The following two associated questions model 63 ÷ 10 = 6 remainder 3.

Question: If I have 63 dollar coins, and ten people to give them to, how many coins does each person get if they are to each have the same number of coins? How many are left over?

Question: If I have 63 dollar coins, how many $10 books can I buy and how many dollars do I have left over?

Properties of Division

Order and brackets cannot be ignored

When multiplying two numbers, the order is unimportant. For example,

3 × 8 = 8 × 3 = 24.

When dividing numbers, however, the order is crucial. For example,

20 ÷ 4= 5, but 4 ÷ 20 =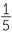

To visualise this calculation, 20 people living in 4 homes means each home has on average 5 people, whereas 4 people living in 20 homes means each home has on average 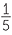of a person.

Similarly when multiplying numbers, the use of brackets is unimportant. For example,

(3 × 4) × 5 = 12 × 5 = 60 and 3 × (4 × 5) = 3 × 20 = 60.

When dividing numbers, however, the use of brackets is crucial. For example,

(24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3; but 24 ÷ (4 ÷ 2)= 24 ÷ 2= 12

Division by zero

Earlier we used empty baskets of apples to illustrate that 5 × 0 = 0.

The same model can be used to illustrate why division by zero is undefined.

If we have 10 apples to be shared equally amongst 5 baskets each basket will have
10 ÷ 5 = 2 apples in each.

If the 10 apples are shared equally between 10 baskets, each basket has 10 ÷ 10 = 1
apples in each.

If 10 apples are shared between 20 baskets, each basket will have an apple in each.

What happens if we try to share 10 apples between 0 baskets? This cannot be done.

If		10 ÷ 0 = a1
		10 ≠ a × 0.

This action is meaningless, so we say that 10 ÷ 0 is undefined.

We must always be careful to relate this to children accurately so that they understand that:

• 10 ÷ 0 is NOT equal to 1 and
• 10 ÷ 0 is NOT equal to 0

but 10 ÷ 0 is not defined.

Dividing by 4, 8, 16, . . .

Because 4 = 2 × 2 and 8 = 2 × 2 × 2, we can divide by 4 and 8, and by all powers of 2, by successive halving.

To divide by 4, halve and halve again. For example, to divide 628 by 4,

628 ÷ 4 = (628 ÷ 2) ÷ 2 = 314 ÷ 2 = 157

To divide by 8, halve, halve, and halve again. For example, to divide 976 by 8,

976 ÷ 8 = (976 ÷ 2) ÷ 2 ÷ 2 = 488 ÷ 2 ÷ 2 = 244 ÷ 2 = 122

Multiplication Algorithm

An algorithm works most efficiently if it uses a small number of strategies that apply in all situations. So algorithms do not resort to techniques, such as the use of near-doubles, that are efficient for a few cases but useless in the majority of cases.

The standard algorithm will not help you to multiply two single-digit numbers. It is essential that students are fluent with the multiplication of two single-digit numbers and with adding numbers to 20 before embarking on any formal algorithm.

The distributive property is at the heart of our multiplication algorithm because it enables us to calculate products one column at a time and then add the results together. It should be reinforced arithmetically, geometrically and algorithmically.

For example, arithmetically we have 6 × 14 = 6 × 10 + 6 × 4, geometrically we see the same phenomenon,

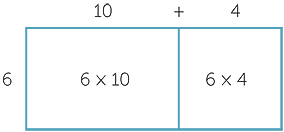
and algorithmically we implement this in the following calculation.

	1	4
×		6
	2	4
	6	0	+
	8	4

Once this basic property is understood, we can proceed to the contracted algorithm.

Introducing the algorithm using materials

Initially when children are doing multiplication they will act out situations using blocks. Eventually the numbers they want to multiply will become too large for this to be an efficient means of solving multiplicative problems. However base-10 materials or bundles of icy-pole sticks can be used to introduce the more efficient method - the algorithm.

If we want to multiply 6 by 14 we make 6 groups of 14 (or 14 groups of 6):

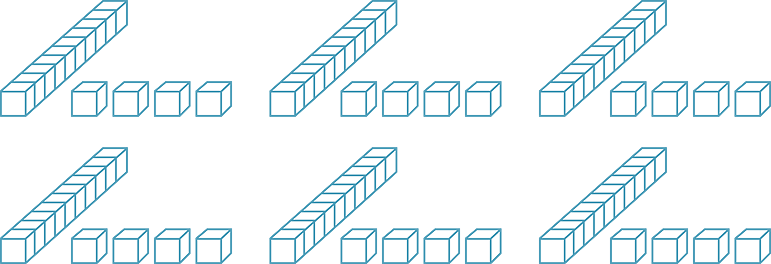
Collect the ‘tens’ together and collect the ‘ones’ together.

This gives 6 ‘tens’ and 24 ‘ones’.

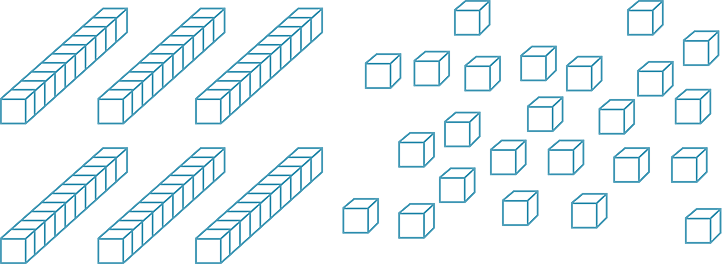
Then make as many tens from the loose ones. There should never be more than nine single ones when representing any number with Base-10 blocks.

This gives 6 ‘tens’ + 2 ‘tens’ + 4 ‘ones’.

We add the tens to get

14 × 6 = 10 × 6 + 4 × 6 = 60 + 20 + 4 = 84

Eventually we should start recording what is being done with the blocks using the multiplication algorithm vertical format. Eventually the support of using the blocks can be dropped and students can complete the algorithm without concrete materials.

Multiplying by a single digit

First we contract the calculation by keeping track of carry digits and incorporating the addition as we go. The previous calculation shortens as either

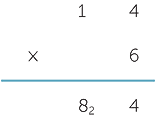
or

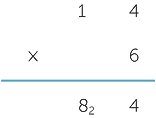
depending on where the carry digits are recorded.

Care should be taken even at this early stage because of the mixture of multiplication and addition. Note also that the exact location and size of the carry digit is not essential to the process and varies across cultures.

Multiplying by a single-digit multiple of a power of ten

The next observation is that multiplying by a single-digit multiple of ten is no harder than multiplying by a single digit provided we keep track of place value. So, to find the number of seconds in 14 minutes we calculate

14 × 60 = 14 × 6 × 10 = 840

and implement it algorithmically as

		1	4
×		6	0
	8	4	0

Similarly, we can keep track of higher powers of ten by using place value to our advantage. So

14 × 600 = 14 × 6 × 100 = 8400

becomes

			1	4
×		6	0	0
	8	4	0	0

For students who have met the underlying observation as part of their mental arithmetic exercises the only novelty at this point is how to lay out these calculations.

Multiplying by a two-digit number

The next cognitive jump happens when we use distributivity to multiply two two-digit numbers together. This is implemented as two products of the types mentioned above. For example,

74 × 63 = 74 × (60 + 3) = 74 × 60 + 74 × 3

is used in the two-step calculation below.

		7	4
×		6	3
	2	2	2
4	4	4	0
4	6	6	2

This corresponds to the area decomposition illustrated below.

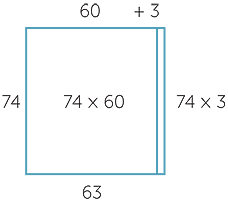
In the early stages, it is worth concurrently developing the arithmetic, geometric and algorithmic perspectives illustrated above.

Unpacking each line in the long multiplication calculation using distributivity explicitly, as in

		7	4
×		6	3
		1	2
	2	1	0
	2	4	0
4	2	0	0
4	6	6	2

corresponds to the area decomposition

It is not efficient to do this extended long multiplication in order to calculate products in general, but it can be used to highlight the multiple use of distributivity in the process. The area model illustration used in this case reappears later as a geometric interpretation of calculations in algebra.

The standard division algorithm

There is only one standard division algorithm, despite its different appearances. The algorithm can be set out as a ‘long division’ calculation to show all the steps, or as a ‘short division’ algorithm where only the carries are shown, or with no written working at all.

Setting the calculation out as a long division

We could set the work out as follows:

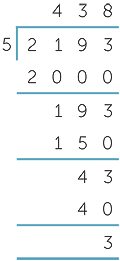5 × 400 = 2000, then subtract 2000 from 2193

5 × 30 = 150, then subtract 150 from 193

5 × 8 = 40, then subtract 40 from 43

The standard ‘long division’ setting-out, however,
allows place value to work for us even more efficiently,
by working only with the digits that are required for
each particular division. At each step another digit is
required − this is usually called ‘bringing down the next digit’.

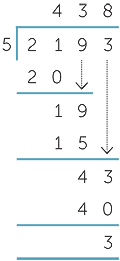Divide 21 by 5.

5 × 4 = 20, then subtract 20 from 21.
Bring down the 9, and divide 19 by 5.

5 × 3 = 15, then subtract 15 from 19.
Bring down the 3, and divide 43 by 5.

5 × 8 = 40, then subtract 40 from 43.

Hence 2193 ÷ 5 = 138 remainder 3.
(Never forget to gather the calculation up into a conclusion.)

The placing of the digits in the top line is crucial. The first step is ‘5 into 21 goes 4’, and the digit 4 is placed above the digit 1 in 21.

Setting the calculation out as a short division

Once the steps have been mastered, many people are comfortable doing each multiplication/subtraction step mentally and writing down only the carry. The calculation then looks like this:

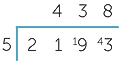		We say,	‘5 into 21 goes 4, remainder 1’.
			‘5 into 19 goes 3, remainder 4’.
			‘5 into 43 goes 8, remainder 3’.

Zeroes in the dividend and in the steps

Zeroes will cause no problems provided that all the digits are kept strictly in their correct columns. This same principle is fundamental to all algorithms that rely on place value.

The example to the right shows the long division and short division calculations for

16 070 ÷ 8 = 2008 remainder 6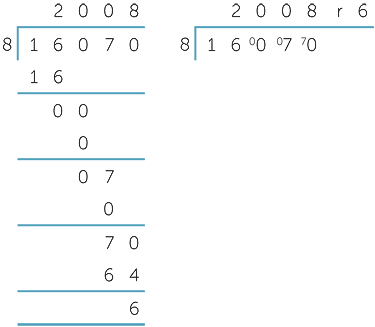

We twice had to bring down
the digit 0, and two of the divisions resulted in a quotient of 0.

 

 

 

 

 

It is possible to extend the division algorithm to divide by numbers of more than one digit. See module, Division of Whole Numbers F to 4.

 

 

 

 

Using the calculator for division with remainder

People often say that division is easily done on the calculator. Division with remainder, however, requires some common sense to sort out the answer.

Calculator assistance may be extremely useful with larger numbers, but experience with long division is essential to interpret the calculator display This phenomenon is common to many similar situations in mathematics.

Links Forward

The first application of multiplication that students are likely to meet is division. When calculating a division, we are constantly calculating multiples of the divisor, and lack of fluency with multiplication is a significant handicap in this process. The material in this module lays the foundation for multiplication, and then division, of fractions and decimals.

Other applications of multiplication include percentages and consumer arithmetic. For example, we calculate the price of an item inclusive of GST by calculating 1.1 times its pre-GST cost.

A familiarity with multiplication and the expression of numbers as products of factors paves the way for one of the major theorems in mathematics.

The Fundamental Theorem of Arithmetic states that every whole number bigger than 1 can be written as a product of prime numbers and such an expression is unique up to the order in which the factors are written.

For example, 24 = 23 × 3 and 20 = 22 × 5.

The Fundamental Theorem of Arithmetic has far-reaching consequences and applications in computer science, coding, and public-key cryptography.

Last, but not least, a strong grounding in arithmetic sets a student up for success in algebra.

The division algorithm uses multiplication and subtraction. As such, division demands that we synthesise a lot of prior knowledge. This is what makes division challenging, and for many students it is their first taste of multi-layered processes. The ability to reflect on what you know, and implement it within a new, higher-level process is one of the generic mathematical skills that division helps to develop.

The implementation of the division algorithm is typically a multi- step process, and as such it helps to develop skills that are invaluable when students move on to algebra. The link to factors is also critical in later years.

History

The product of two numbers is the same no matter how you calculate it or how you write your answer. Just as the history of number is really all about the development of numerals, the history of multiplication and division is mainly the history of the processes people have used to perform calculations. The development of the Hindu-Arabic place-value notation enabled the implementation of efficient algorithms for arithmetic and was probably the main reason for the popularity and fast adoption of the notation.

The earliest recorded example of a division implemented algorithmically is a Sunzi division dating from 400AD in China. Essentially the same process reappeared in the book of al Kwarizmi in 825AD and the modern-day equivalent is known as Galley division. It is, in essence, equivalent to modern-day long division. However, it is a wonderful example of how notation can make an enormous difference. Galley division is hard to follow and leaves the page a mess compared to the modern layout.

The layout of the long division algorithm varies between cultures.

Throughout history there have been many different methods to solve problems involving multiplication. Some of them are still in use in different parts of the world and are of interest to teachers and students as alternative strategies or because of the mathematical challenge involved in learning them.

Italian or lattice method

Another technique, known as the Italian or lattice method is essentially an implementation of the extended version of the standard algorithm but in a different layout. The method is very old and might have been the one widely adopted if it had not been difficult to print. It appears to have first appeared in India, but soon appeared in works by the Chinese and by the Arabs. From the Arabs it found its way across to Italy and can be found many Italian manuscripts of the 14th and 15th centuries.

The multiplication 34 × 27 is illustrated here.

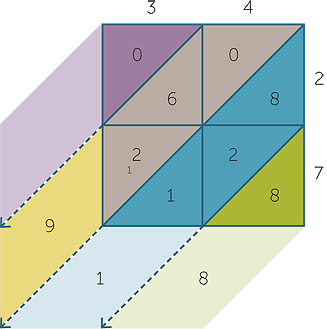
34 × 27 = 918

In the top right rectangle 4 × 2 is calculated. The digit 8 is placed in the bottom triangle and 0 in the top triangle.

Then 3 × 2 is calculated and the result entered as shown.

In the bottom right rectangle 4 × 7 is calculated. The digit 8 is placed in the bottom triangle and the digit 2 in the top triangle. The result of 3 × 7 is also recorded in this way.

The green diagonal contains the units.

The blue diagonal contains the tens.

The orange diagonal contains the hundreds.

The digits are now summed along each diagonal starting from the right and each
result recorded as shown. Note that there is a ‘carry’ from the ‘tens diagonal’ to the ‘hundreds diagonal’

References

A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)

History of Mathematics, D. E. Smith, Dover publications New York, (1958)

Knowing and Teaching Elementary Mathematics: teachers’ understanding of fundamental mathematics in China and the United States. Liping Ma, Mahwah, N.J.: Lawrence Erlbaum Associates, (1999)

History of Mathematics, Carl B. Boyer (revised by Uta C. Merzbach), John Wiley and Sons, Inc., (1991)

ANSWERS TO EXERCISES

Exercise 1

a	9 × 32	= 9 × 30 + 9 × 2
		= 270 + 18
		= 2888

b	31 × 8	= 30 × 8 + 1 × 8
		= 240 + 8
		= 248

c	102 × 8	= 100 × 8 + 2 × 8
		= 800 + 16
		= 816

Exercise 2

a

3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42. Hence 42 ÷ 3 = 14.

b

11, 22, 33, 44, 55. Hence 55 ÷ 11 = 5.

c

100, 200, 300, 400, 500, 600, 700, 800, 900, 1000. 1000 ÷ 100 = 10.

Exercise 3

a

8 = 2 × 4 and 8 ÷ 4 = 2.

b

56 ÷ 8 = 7 and 56 ÷ 7 = 8.

c

81 = 9 × 9 and 81 ÷ 9 = 9. Because the divisor and the quotient are the same, the multiplication statement becomes a statement about squaring, and the other corresponding division statement is the same as the original statement.

Exercise 4

a

24÷ 4 = 6. If 24 children are divided into groups of 4, how many groups are there?

b

20 ÷ 2 = 10. If 20 metres of fabric is divided into two equal pieces, how long is

c

160 ÷ 10 =16. If 160 books are bundled into packages of 10 each, how many packages are there?

d

35÷7 = 5. If a 35-day period is divided into 7 equal periods, how long is each period?

Exercise 5

a

Twelve 7-person rescue teams can be formed, with 6 people to spare. How many people will be in 7 equal groups formed from 90 people? There will be 12 people in each group, with 6 left over.

b

Nine 5-seater cars are needed, and there will be two spare seats. How many people will be in 5 equal groups formed from 43 people? There will be 8 groups, with 3 people left over.

Exercise 6

a

246 ÷ 4 = (246 ÷ 2) ÷2 = 123 ÷ 2 = 61

b

368 ÷ 8 = ((368 ÷2) ÷ 2) ÷ 2 = (184 ÷ 2) ÷2 = 92 ÷ 2= 46.

c

163 ÷ 8 = ((163 ÷ 2) ÷ 2)÷2 =81 ÷ 2 = 40 ÷ 2 = 20.

d	12 048 ÷ 16	= (((12 048 ÷ 2) ÷ 2 ÷ 2) ÷ 2 = ((6024 ÷ 2) ÷ 2) ÷ 2
		= (3012 ÷ 2) ÷ 2 = 1506 ÷ 2 = 752.

 

The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.

The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.

© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/