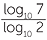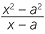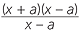The Improving Mathematics Education in Schools (TIMES) Project
- Knowledge of the index laws for positive integer powers.
- Facility with the arithmetic of integers and fractions.
- Facility with basic algebra.
- Familiarity with rounding numbers correct to a given number of decimal places.
Indices provide a compact algebraic notation for repeated multiplication. For example, is it much easier to write 35 than 3 × 3 × 3 × 3 × 3.
Once index notation is introduced the index laws arise naturally when simplifying numerical and algebraic expressions. Thus the simplificiation 25 × 23 = 28 quickly leads
to the rule am × an = am + n, for all positive integers m and n.
As often happens in mathematics, it is natural to ask questions such as:
- Can we give meaning to the zero index?
- Can we give meaning to a negative index?
- Can we give meaning to a rational or fractional index?
These questions will be considered in this module.
In many applications of mathematics, we can express numbers as powers of some given base. We can reverse this question and ask, for example, ‘What power of 2 gives 16? Our attention is then turned to the index itself. This leads to the notion of a logarithm, which is simply another name for an index.
Logarithms are used in many places:
- decibels, that are used to measure sound pressure, are defined using logarithms
- the Richter scale, that is used to measure earthquake intensity, is defined using logarithms
- the pH value in chemistry, that is used to define the level of acidity of a substance,
is also defined using the notion of a logarithm.
When two measured quantities appear to be related by an exponential function, the parameters of the function can be estimated using log plots. This is a very useful tool in experimental science.
Logarithms can be used to solve equations such as 2x = 3, for x.
In senior mathematics, competency in manipulating indices is essential, since they are used extensively in both differential and integral calculus. Thus, to differentiate or integrate a function such as 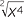 , it is first necessary to convert it to index form.
, it is first necessary to convert it to index form.
The function in calculus that is a multiple of its own derivative is an exponential function. Such functions are used to model growth rates in biology, ecology and economics, as well as radioactive decay in nuclear physics.
We recall that a power is the product of a certain number of factors, all of which are the same. For example, 37 is a power, in which the number 3 is called the base and the number 7 is called the index or exponent.
In the module, Multiples, Factors and Powers, the following index laws were established for positive integer exponents. So positive integers and , and rational numbers and , we have:
Index Laws
- 1
- To multiply powers with the same base, add the indices.
aman = am+n.
- 2
- To divide powers with the same base, subtract the indices.
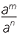 = am − n, (provided m > n.)
= am − n, (provided m > n.)
- 3
- To raise a power to a power, multiply the indices.
(am)n = amn. - 4
- A power of a product is the product of the powers.
(ab)m = ambm. - 5
- A power of a quotient is the quotient of the powers.


 m=
m= 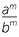 , (provided b ≠ 0.)
, (provided b ≠ 0.)
These laws also hold when a and b are real.
EXERCISE 1
Show that 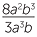 ÷
÷ 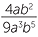 = 6ab5.
= 6ab5.
We now seek to give meaning to other types of exponents. The basic principle we use throughout is to choose a meaning that is consistent with the index laws above.
The Zero Index
Clearly 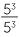 = 1. On the other hand, applying index law 2, ignoring the condition m > n,
= 1. On the other hand, applying index law 2, ignoring the condition m > n,
we have 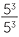 = 50. If the index laws are to be applied in this situation, then we need to define 50 to be 1.
= 50. If the index laws are to be applied in this situation, then we need to define 50 to be 1.
More generally, if a ≠ 0 then we define a0 = 1.
Note that 00 is not defined. It is sometimes called an indeterminant form.
(The explanation of this term is that one can find sequences of numbers of the form ab in which both a and b approach 0, but where the limit of the sequence is not 1 and indeed can be made to be any number we like, by a suitable choice of and For example, the terms of the sequence
![]() 1,
1,  0,
0,  0,
0, 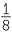 0,…
0,…
are all equal to 1, while the terms of the sequence
![]() 01, 0
01, 0 , 0
, 0 , 0
, 0 , …
, …
are all equal to 0. In each case the form of the terms approaches 00.
A similar situation occurs with  and so the expression
and so the expression 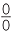 is also often referred to as an indeterminant form.
is also often referred to as an indeterminant form.
EXAMPLE
(3a2b)0 = 1, assuming a and b are not zero.
The index laws also hold for the zero index.
Negative Exponents
If we examine the pattern formed when we take decreasing powers of 2, we see
![]() 24 = 16, 23 = 8, 22 = 2, 21 = 2, 20 = 1, 2−1 = ?, 2−2 = ?
24 = 16, 23 = 8, 22 = 2, 21 = 2, 20 = 1, 2−1 = ?, 2−2 = ?
At each step as we decrease the index, the number is halved. Thus it is sensible to define
![]() 2−1 =
2−1 =  .
.
Furthermore, continuing the pattern, we define
![]() 2−2 =
2−2 =  =
= 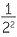 , 2−3 =
, 2−3 = 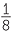 =
= 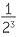 , and so on.
, and so on.
These definitions are consistent with the index laws.
For example, 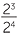 = 23 − 4 = 2−1. But clearly,
= 23 − 4 = 2−1. But clearly, 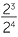 =
=  .
.
Similarly, 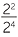 = 22 − 4 = 2−2. but clearly,
= 22 − 4 = 2−2. but clearly, 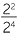 =
=  =
= 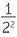 .
.
We can confirm our intuition by considering and .
In general, for any non-zero number , and positive integer , we define
![]() a−1 =
a−1 =  and a−n =
and a−n = 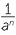 .
.
Note that all the earlier index laws also hold for negative indices.
EXAMPLE
Simplify
a![]() 8−2
8−2 ![]() b
b![]()

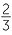
 −3
−3 ![]() c
c![]()
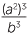 ÷
÷ 
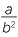
 −2
−2
Solution
a![]() 8−2 =
8−2 = 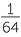
![]() b
b![]()

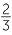
 −3=
−3= 

 3 =
3 = 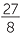
c![]()
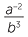 ÷
÷ 
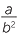
 −2 =
−2 = 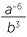 ÷
÷  =
= 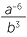 ×
× 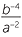 = a−4b−7 =
= a−4b−7 = 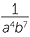
Notice that


 −1 =
−1 = 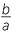
- When asked to simplify an expression involving indices, we generally express our answer using positive indices.
EXERCISE 2
Simplify 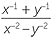 .
.
| For all intergers m and n and non-zero numbers a and b the following are true. | ||
| Zero exponent | a0 = 1 | |
| Negative exponent |
a−n = 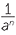
|
|
| Index law 1 | Product of power | aman = am+n |
| Index law 2 | Quotient of power |
am ÷ an = 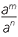 = am − n = am − n
|
| Index law 3 | Power of a power | (am)n = amn |
| Index law 4 | Power of a product | (ab)n = anbn |
| Index law 5 | Power of a quotient |
   n = n = 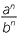
|
Fractional Indices
We now extend our study of indices to include rational or fractional exponents. In particular, can we give meaning to 4 ?
?
Once again, we would like the established index laws to hold. Hence, squaring this expression we would like to say:
![]()
 4
4
 2 = 4
2 = 4 × 2 = 41 = 4.
× 2 = 41 = 4.
Thus we define 4 to be
to be ![]() = 2.
= 2.
In general we define a =
= ![]() for any positive number a.
for any positive number a.
Note that we have defined a to be the positive square root of We do this so that there is only one value for a
to be the positive square root of We do this so that there is only one value for a .
.
Applying a similar argument, for consistency with the index laws, we define a =
= ![]() ,
,
a =
= ![]() , and so on.
, and so on.
In general, for any positive integer n and positive number a, define a =
= ![]() .
.
EXAMPLE
27 = 3, 16
= 3, 16 = 2, (a6)
= 2, (a6) = a4.
= a4.
Assuming consistency with index law 3, we can write  8
8
 2 = 8
2 = 8 × 2 = 8
× 2 = 8 . But 8
. But 8 =
= ![]() = 2.
= 2.
Thus, 8 = 4.
= 4.
The notation 8 means ‘the square of the cube root of 8’ which is equal to 4.
means ‘the square of the cube root of 8’ which is equal to 4.
Note that we could also have expressed this as the ‘cube root of the square of 8’, which is, of course, also equal to 4, that is:
- 8
 =
=  =
=  = 4 or,
= 4 or, - 8
 = (
= (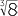 )2 = 22 = 4.
)2 = 22 = 4.
In general, if is a positive number and are positive integers, we define
![]() a
a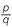 =
=  a
a
 p or
p or ![]() .
.
In words, we take the qth root of a and raise it to the power p.
EXAMPLE
Find ![]() a
a![]() 16
16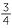
![]() b
b![]()

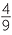


Solution
a![]() 16
16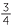 = (
= (![]() )3 = 23 = 8
)3 = 23 = 8 ![]() b
b![]()

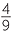

 =
= 
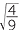
 3 =
3 = 
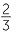
 3 =
3 = 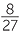 .
.
Negative fractional indices
Finally, we can extend the indices to include negative rationals. For example,
![]() 8−
8− =
=  8
8
 −1 =
−1 =  =
=  .
.
So that
![]() a
a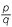 =
= 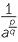 .
.
EXERCISE 3
Show that:![]() 32−
32− =
=  ,
, ![]()


 −
− =
=  ,
, ![]()
 2x−
2x−
 5 =
5 = 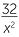 .
.
We have now defined ax for any positive real number a and any rational number x.
It remains to check that the index laws also hold in this more general case. We will not go through the details. The following example outlines how this might be done in one particular case.
EXERCISE 4
This exercise asks you to give a proof that the first index law holds for negative integer exponents and also for fractional exponents.
a![]() By writing a−pa−q as
By writing a−pa−q as  ×
× 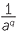 , show that a−pa−q = a−p −q as, where p, q are positive integers.
, show that a−pa−q = a−p −q as, where p, q are positive integers.
b![]() By writing as show that a
By writing as show that a × a
× a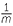 as a
as a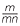 × a
× a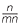 =
=  m ×
m ×  n, show that a
n, show that a × a
× a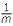 = a
= a +
+ 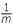 .
.
It is possible to give similar proofs that the other index laws also hold for negative integer and rational exponents.
Scientific notation, or standard form, is a convenient way to represent very large or very small numbers. It allows the numbers to be easily recorded and read.
The star Sirius is approximately 75 684 000 000 000 km from the sun. We can represent this number more compactly by moving the decimal point to just after the first non-zero digit and multiplying by an appropriate power of 10 to recover the original number. Thus
![]() 75 684 000 000 000 = 7.5684 × 1013.
75 684 000 000 000 = 7.5684 × 1013.
If we move the decimal point 13 places to the right, inserting the necessary zeroes, we arrive back at the number we started with.
We can similarly deal with very small numbers using negative indices. For example, an Angstrom (Å) is a unit of length equal to 0.000 000 000 1 m, which is the approximate diameter of a small atom. We place the decimal point just after the first non-zero digit and multiply by the appropriate power of ten. Thus,
0.000 000 000 1 = 1 × 10−10. Hence, for example, the diameter of a uranium atom is 0.000 000 000 38 m which we may write as 3.8 × 10−10 m or 3.8 Å.
The index laws may be used to perform operations on numbers written in scientific notation.
EXAMPLE
Simplify (3.14 × 10−2)3 ÷ (7.1 × 10−8) giving your answer correct to one decimal place.
Solution
(3.14 × 10−2)3 ÷ (7.1 × 10−8) = (3.143 ÷ 7.1) × 102 ≈ 4.36044 × 102 ≈ 436.0 correct to 1 decimal place. In this case, we could leave this as the answer, or, if required, write is as 4.36 × 102.
Significant figures in scientific notation
Scientists and engineers routinely employ scientific notation to represent large and small numbers. Since all measurements are approximations anyway, they generally report the numbers rounded to a given number of significant figures. Thus, a number such as 2.1789 × 107 could be written as approximately 2.18 × 107. This is the same as rounding the number 21 789 000 to 21 800 000, that is, correct to three significant figures.
A given number may be expressed with different numbers of significant figures. For example, 3.1 has 2 significant figures, 3.14 has 3 significant figures and so on. To round a number to a required number of significant figures, first write the number in scientific notation and identify the last significant digit required. Then leave the digit alone if the next digit is 0, 1, 2 ,3 or 4 (in this case the original number is rounded down) and increase the last digit by one if the next digit is 5, 6, 7, 8 or 9 (in this case the original number is rounded up.)
EXERCISE 5
Use a calculator to find 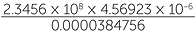 correct to 4 significant figures.
correct to 4 significant figures.
We can use the calculator to find approximate values of for various rational values of 2x. We place these in a table and we can then plot the ordered pairs (x, 2x)to produce a graph of y = 2x.
EXAMPLE
Produce a table of values for the function y = 2x and use it to draw its graph.
Solution
A table of approximate values follows:
| x | -3 | −2.5 | −2 | −1.5 | −1 | −0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| y | 0.125 | 0.177 | 0.25 | 0.354 | 0.5 | 0.707 | 1 | 1.414 | 2 | 2.828 | 4 | 5.657 | 8 |
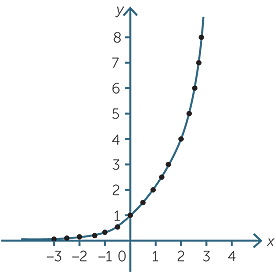
Note that although we have ‘joined the dots’ to form a smooth curve, we have not given any meaning at this stage to 2x when is an irrational number. We cannot deal with this problem at this stage.
We note the following features of the graph.
- the graph is increasing.
- the values increase quite rapidly as we move along the axis.
- on the left hand-side, the graph approaches, but never reaches, the axis.
EXERCISE 6
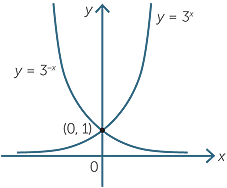
Draw the graphs of y = 3x and y = 3−x on the set of axes.
An exponential equation is an equation in which the pronumeral appears as an index.
For example, 23x = 64 is an exponential equation.
We can see from the graph that the curve y = 23x and y = 64 the line only meet once,
so there is one unique solution to the exponential equation.
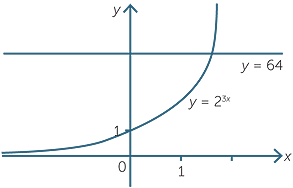
We can solve the equation as follows:
23x = 64
Hence 3x = 6, giving x = 2.
EXAMPLE
| a |
2x = 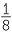 |
b |
7x = 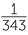 |
c |
7x = 1 |
d |
81x = 243 |
Solution
| a |
2x = 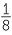 |
b |
7x = 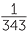 |
c |
7x = 1 | d |
81x = 243 | ||||||||||||||||
| since, | 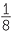 |
= 2–3 | since, | 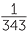 |
= 7–3 | since, | 70 | = 1 | since, | (34)x | = 35 | ||||||||||||
| 2x | = 2–3 | 7x | = 7–3 | x | = 0 | 4x | = 5 | ||||||||||||||||
| x | = –3 | x | = –3 | x | =  |
||||||||||||||||||
EXERCISE 7
Solve 33 − x = 27x − 1.
How do we solve 2x = 7? The method used above does not work in quite the same way, since we do not know how to express 7 as a power of 2.
We will revisit this problem after we have looked at logarithms.
The exponential function is used to model growth − generally population growth in biology, but this may also include the growth of money via compound interest.
Suppose that a culture initially contains 1000 bacteria and that this number doubles
each hour. Thus, after
- one hour there are 1000 × 2 bacteria
- two hours there are 1000 × 2 × 2 = 1000 × 22 bacteria
- three hours there are 1000 × 22 × 2 = 1000 × 23 bacteria
and so on.
Following the pattern, if there are bacteria after hours then
![]() N = 1000 × 2t.
N = 1000 × 2t.
This is an example of exponential growth.
Exponentials can also be used to model radioactive decay. Radioactivity is a natural phenomenon in which atoms of one element ‘decay’ to form atoms of another element by emitting a particle such as an alpha particle.
EXAMPLE
A sample of a radioactive substance with an initial mass of 100g decays over time, halving every hour. Find a formula for the amount, M g, present after hours.
Solution
After 1 hour, the mass is 100 ×  g.
g.
After 2 hours, the mass is 100 ×  ×
×  = 100 ×
= 100 × 

 2g.
2g.
After 3 hours, the mass is 100 × 

 2 ×
2 ×  = 100 ×
= 100 × 

 3g.
3g.
Following this pattern, there are
M = 100 × 

 t g of the radioactive substance after hours.
t g of the radioactive substance after hours.
A table is constructed below and the graph is plotted.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| M | 100 | 50 | 25 | 12.5 | 6.25 | 3.13 | 1.56 |
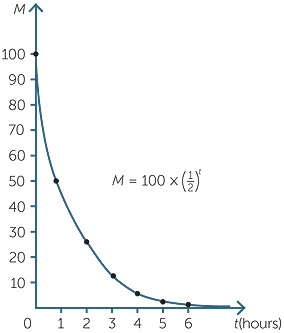
This is an example of exponential decay.
Exponential formulas have the form
P = A × Bt, where A, B are positive constants. If
- B > 1, we say that P grows exponentially,
- B < 1 we say that P decays exponentially.
EXERCISE 8
For the rule y = 20 × 3t:
a![]() Complete the table of values.
Complete the table of values.
| t | 0 | 1 | 2 | 3 |
| y |
b![]() Plot the graph of y against t.
Plot the graph of y against t.
c![]() Find the value y, correct to 2 decimal places, when:
Find the value y, correct to 2 decimal places, when:
![]() i
i![]() t = 0.5
t = 0.5![]() ii
ii![]() t = 2.5
t = 2.5 ![]() iii
iii![]() t = 2.8
t = 2.8
It is easy to find values of x, such that 2x = 2 or 2x = 4, or 2x = 32. On the other hand, how do we solve the equation 2x = 10?
Problems such as this arise naturally when we deal with exponential growth and decay.
In the example above, we gave the formula for the mass of a radioactive substance to be M = 100 × 

 t g.
t g.
If we ask the question, when is the mass equal to say 30g, then we need to solve 

 t = 0.3 to find the time.
t = 0.3 to find the time.
Just as taking a square root is the inverse process to squaring, taking a logarithm is the inverse process to taking a power.
Since 23 = 8, we say that log2 8 = 3. That is, the logarithm is the index in the equation
23 = 8. We read this as ‘the log of 8 to the base 2 is 3.’
To find the logarithm of a number a to the base b, we ask the question ‘what power do I raise b to, in order to obtain a?
So, to find for example, log3 243, we recall that 243 = 35, so log3 243 = 5.
EXAMPLE
Find log8 4.
Solution
One approach is to write, log8 4 = x and so 4 = 8x. Since both numbers are powers of 2, we can write 22 = (23)x = 23x.
Equating indices, 3x = 2, so x = 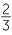 .
.
Thus, log8 4 =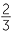 .
.
(Indeed, 8 = (
= (![]() )2 = 22 = 4.)
)2 = 22 = 4.)
The relationship connecting logarithms and powers is:
![]() x = loga y means y = ax.
x = loga y means y = ax.
The number is called the base and must be a positive number. Also since ax is positive, we can only find the logarithm of a positive number. We will assume from now on that both are positive, but can be negative.
EXERCISE 9
Find the value of x.
| a |
b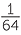 = x = x |
c |
||
| d |
e |
f |
Note: The following identities exemplify the inverse operations of taking a power and taking a logarithm. These need to be properly understood by students.
For x > 0,
![]() 2log2 x = x.
2log2 x = x.
More generally, for a > 0, x > 0,
![]() aloga x = x.
aloga x = x.
In the other direction, for any x,
![]() loga 2x = x.
loga 2x = x.
More generally, for a > 0,
![]() loga ax = x.
loga ax = x.
It is important for students to properly understand these two general identities.
Logarithms to the base 10
You will notice that in all the examples above, the values of the logarithms were rational numbers, which were not too hard to find. Suppose we wanted to know the value of
log10 7? Thus, we seek a number x such that 7 = 10x.
We can see from the graph of y = 10x that such a number lies between 0 and 1.
The calculator is able to give an approximate value of this number. It is shown in the module, The Real Numbers that numbers such as this are irrational.
Thus, to 4 decimal places, the calculator reports that log10 7 ≈ 0.8451.
The Logarithm Laws
Suppose a > 0 for the rest of this section.
- Law 1
- loga = 0 and loga a = 1
since a0 = 1, we have loga 1 = 0.
Similarly, since a1 = a, we have loga a = 1.
- Law 2
- If x and y are positive numbers, then loga xy = loga x + loga y
That is, the logaithm of a product is the sum of the logarithms.
Suppose x = ac and y = ad so that loga x = c and loga y = d.
| Then | xy | = ac × ad | ||||
| =ac+d | (by Index law 1) | |||||
| So | loga xy | = loga ac+d | ||||
| = c + d | ||||||
| = loga x + loga y | ||||||
- Law 3
- If x and y are positive numbers, then loga
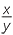 = loga x − loga y.
= loga x − loga y.
That is, the logarithm of a quatient is the difference of their logarithms.
Suppose x = ac and y = ad so that loga x = c and loga y = d.
| Then |  |
= 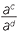 |
||||
| = ac−d | (by Index law 2) | |||||
| So | loga 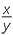 |
= loga ac−d | ||||
| = c − d | ||||||
| = loga x + loga y | ||||||
- Law 4
- If x is a positive number, then loga
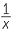 = −loga x.
= −loga x.
This follows from logarithm law 3 and logarithm law 1.
loga  |
= loga 1 − loga x | (logarithm law 3) | ||
| = 0 − loga x | (logarithm law 1) | |||
| = −loga x, as required. | ||||
- Law 5
- If x is a positive number and n is any rational number, then loga (xn) = nloga x.
This follows from logarithm law 3 and logarithm law 1.
| loga (xn) | = loga ((ac)n) | |||
| = loga (acn) | (by Index law 3) | |||
| = nloga x, as required. | ||||
EXAMPLE
Given log7 2 = α, log7 3 = β and log7 5 = , express in termd of α, β and
, express in termd of α, β and  :
:
a![]() log7 6
log7 6 ![]() b
b![]() log7 6
log7 6 ![]() c
c![]() log7
log7 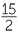
solution
| a | log7 6 | = log7 (2 × 3) | b | log7 6 | = log7 (3 × 25) | |||
| = log7 2 + log7 3 | = log7 3 + log7 52 | |||||||
| = α + β | = β + 2 |
|||||||
| c | log7 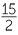 |
= log7 15 − log7 2 | ||||||
| = log7 (3 × 5) − log7 2 | ||||||||
| = log7 3 + log7 5 − log7 2 | ||||||||
| = β + |
EXERCISE 10
Simplify:
a![]() logb x2 + logb x3 − logb x4
logb x2 + logb x3 − logb x4 ![]() b
b![]() logk
logk  + logk
+ logk 
c![]() logb (x2 − a2) − logb (x − a), if x > a
logb (x2 − a2) − logb (x − a), if x > a
Change of base
Some calculators are able to find the logarithm of a number to any positive base. This is not, however, universal, and there are many occasions when we would like to change from one base to another.
For example, to find log3 7 we can change from base 3 to base 10, where the calculator can be used. Change of base is also important in calculus, where logarithms to the base are used.
The change of base formula states that:
logb c = 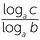
Here is a proof of this result.
Let x = logb c, then c = bx.
Take logarithms to the base of both sides, then
loga c = loga bx = xloga b (using logarithm law 5).
Hence x = 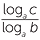 . That is logb c =
. That is logb c = 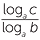 .
.
EXAMPLE
Calculate log7 8 to four decimal places.
Solution
Changing form base 7 to base 10.
| log7 8 | = 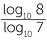 |
| ≈ 1.0686 |
As a check, with the calculator, 71.0686 ≈ 7.9997.
The Logarithm graph
As we did for exponentials, we can draw the graph of y = log2 x by drawing up a table of values.
| x |  |
 |
 |
 |
1 | 2 | 4 | 8 | 16 |
| y | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 |
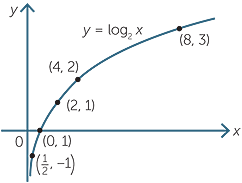
We note the following features of the graph:
- the graph is to the right of the y-axis, since only logarithms of positive numbers are defined.
- as becomes small, the y values become large negative numbers. Thus, the graph approaches, but does not touch, the negative axis. We say that the negative y-axis is
an asymptote of the graph. - the x-intercept is (1, 0) since log2 1 = 0.
- the graph does not have a y-intercept.
- as x takes large positive values, log2 x becomes large.
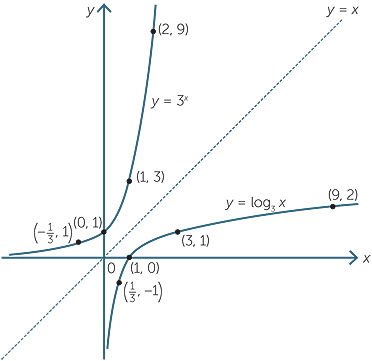
Logarithms and exponentials are inverses of each other. Their graphs are reflections of each other in the line y = x.
This is illustrated in the following graphs of y = log3 x and y = 3x.
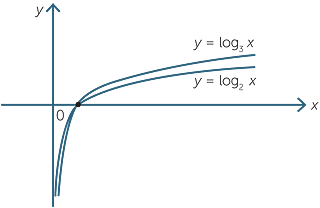
EXERCISE 11
Use a table to draw on the same diagram the graphs of y = log2 x and y = log3 x. What can you say about the graphs when x < 1 and x > 1 when ?
Using Logarithms to solve exponential equations
We will conclude this module with some further applications of exponentials and logarithms.
Earlier in the module we raised the question of solving 2x = 7. If we have a calculator that finds logarithms to the base 2, we can solve this equation by re-writing it using logarithms,
|
2x = 7 |
|
|
So, x = log2 7 ≈ 2.807 (correct to 3 dec. places.) |
|
|
If the calculator only has logarithms to the base 10, we can use the change of base form to write |
|
|
log2 7 = |
|
Alternatively, we can take the logarithms to the base 10 of both sides and use the logarithm laws.
![]() 2x = 7
2x = 7
![]() log10 2x = log10 7
log10 2x = log10 7
![]() xlog10 2 = log10 7 (using the logarithms law)
xlog10 2 = log10 7 (using the logarithms law)
Hence, x = 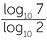 ≈ 2.807 (correct to 3 dec. places.)
≈ 2.807 (correct to 3 dec. places.)
(Note that this is equivalent to changing the base from 7 to 10.)
EXERCISE 12
The following numbers exceed the capacity of your calculator. By taking logarithms of each number to the base 10, decide which is larger, 1023451 or 1023352.
EXAMPLE
A culture of bacteria initially has a mass of one gram and triples in size every hour.
How long will it take to reach a mass of 20 grams?
Solution
Let y grams be the mass of the culture after t hours, then y = 3t.
| If y = 20 then 20 = 3t. | |||
| log10 20 | = log10 3t | ||
| log10 20 | = tlog10 3 | ||
| t | = |
||
| ≈ 2.727 hours | |||
| ≈ 2 hours 44 minutes | |||
It will take approximately 2 hours 44 minutes for the mass to reach 20 gram.
Compound Interest
In the module, Consumer Arithmetic the compound interest formula
![]() An = P(1 + R)n
An = P(1 + R)n
was introduced, where An was the amount that an initial investment P is worth after n units of time, when compounded at an interest rate R.
In many applications of this formula, we need to find the value of n. This can be done using logarithms.
EXAMPLE
$50 000 is invested on Jan 1 2008 at 8% per annum. Interest is only paid on Jan 1 of each year. After how many years will the investment be worth:
a![]() $75 000
$75 000 ![]() b
b![]() $100 000?
$100 000?
Solution
- a
- a An = P(1 + R)n
An = 75 000, P = 50 000 and R = 0.08
75 000 = 50 000(1.8)n
 = (1.8)n
= (1.8)n
Take logarithm of both sides.
log10 = nlog10 (1.08)n
= nlog10 (1.08)n
n =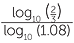
= 5.26844...
At the end of the sixth year the investment will be worth $50 000(1.08)5 = $73 343.72.
At the end of the fifth year the investment will be worth $50 000(1.08)5 = $73 466.40.
The investment will worth more than $75 000 at the end of the sixth year. - b
- An = P(1 + R)n
An = 100 000, P = 50 000 and R = 0.08
100 000 = 50 000(1.8)n
2 = (1.8)n
Take logarithm of both sides.
log10 (2) = nlog10 (1.08)n
n =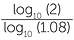
= 9.00646...
At the end of the tenth year the investment will be worth
$50 000(1.08)10 = $107 946.25.
At the end of the ninth year the investment will be worth
$50 000(1.08)10 = $99 950.23.
The investment will worth more than $100 000 at the end of the sixth year.
EXERCISE 13
An amount of $100,000 is invested at an annual interest rate of 6.25%. If the interest is calculated yearly, how long before the investment has reached $150, 000? What is the answer if the interest is paid monthly?
Irrational Indices
In this module we have extended the meaning of ab to include all rational values of b.
It is thus pertinent to ask: ‘What about an expression such as 3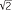 ?’
?’
Can this be given any meaning? After all, if you enter this into a calculator an answer is produced − but what does the answer actually mean? The calculator is, of course, simply approximating ![]() by a rational number. So if we approximate
by a rational number. So if we approximate ![]() by 1.414 =
by 1.414 =  , this would produce the number 3
, this would produce the number 3 , which has the usual meaning as outlined in this module. Its value is approximately 4.7277 (correct to four decimal places.) This however does not equal 3
, which has the usual meaning as outlined in this module. Its value is approximately 4.7277 (correct to four decimal places.) This however does not equal 3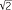 , but it does give us a hint as to how we might give this number meaning.
, but it does give us a hint as to how we might give this number meaning.
One way to define 3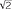 is to think of it as the limit of a sequence of approximations, each one obtained by taking better and better approximations to
is to think of it as the limit of a sequence of approximations, each one obtained by taking better and better approximations to ![]() and proceeding as above. Thus
and proceeding as above. Thus
31.4 ≈ 4.6555, 31.41 ≈ 4.7070, 31.414 ≈ 4.7277 and so on.
This is not, of course, as satisfying as the definitions we gave for rational powers.
An alternative, but equivalent definition for real powers can be given once the exponential function and the natural logarithm have been introduced. In general, for any real number b and positive real number a, we can define ab to be eblog a, where the logarithm is to the base e. Thus, 3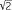 = e
= e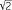 log 3 ≈ 4.7288 correct to 4 decimal places.) Note that this is consistent with the logarithm law alog b = log ab and also the inverse relationship between exponentials and logarithms elog x = x.
log 3 ≈ 4.7288 correct to 4 decimal places.) Note that this is consistent with the logarithm law alog b = log ab and also the inverse relationship between exponentials and logarithms elog x = x.
This definition is also used for exponents involving complex numbers, but there the situation becomes more complicated and is best left until tertiary study.
The Natural Logarithm and the number e
In senior mathematics, the so-called natural logarithm loge x, also written as ln x, or simply as log x, arises when we try to integrate the expression  .
.
Thus 
 dt = loge x.
dt = loge x.
The base of this logarithm is the irrational number e ≈ 2.71828.
The functions y = ex and y = loge x are inverse functions, so that elog x = x, for x > 0, and loge ex = x, for all real x. These functions are central to an understanding of exponential growth (used to model populations and compound interest) as well as radioactive decay and other physical processes. Thus, they arise is chemistry, biology, economics, finance, and statistics as well as physics and engineering.
Index notation is comparatively modern. The Greek writer Diophantus used the symbol to denote what we would call x2 and K for x3. In medieval algebra, Q and C were used instead. Even in the 16th century, people were still writing xxx for x3 but our modern notation is clearly evident in Maclaurin’s Treatise on Algebra (1779).
Although conceptually, logarithms are implicit in some of the early Indian mathematics, it was John Napier’s book Mirifici Logarithmorum Canonis Descriptio in 1614, that formally introduced the concept and name. (The word is a combination of the Greek words logos and arithmos, and thus literally means number reckoning.
Until the advent of the modern calculator, logarithms were used extensively to aid in complicated arithmetic calculations. This use continued in schools until the early 1980’s, when cheap scientific calculators became available.
Thus, for example, to find 23.14 × 0.4526, each number was converted to its logarithm base 10 (there were tables and methods to do this). These were added and the result was raised to the power 10, using so-called anti-logarithm tables, to produce the required answer. This method exploited the index law, log10 xy = log10 x + log10 y.
To perform a division such as 23.14 ÷ 0.4526, the logarithms were subtracted.
To find, for example, ![]() the logarithm to the base 10 of 463.2 was divided by 5 and then the table of anti-logarithms was applied to find the answer. This used the result,
the logarithm to the base 10 of 463.2 was divided by 5 and then the table of anti-logarithms was applied to find the answer. This used the result,
log10 ![]() = log10 a
= log10 a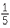 +
+ 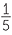 log10 a.
log10 a.
In addition logarithm tables of the trigonometric ratios were available to assist with trigonometric calculations.
pH Values
Logarithms to the base 10 are still used extensively in chemistry. The measure of acidity of a solution is called its pH value. Acidity is connected to the the molar concentration of dissolved hydronium ions (H3O+), and the pH of a solution is the negative of the logarithm of this quantity. The modern definition was introduced in 1924. A pH of 7, corresponding to a molar concentration of 10−7, is called neutral and is the pH of water. The closer to 0, the more acidic a solution is, while a pH closer to 14 tells us that the solution is alkaline.
Log plots
When a collection of data is plotted and the scientist suspects that there is an exponential relationship between the two quantities being plotted, then a log plot can be used.
Thus, if the two quantities x, y are related by y = ax + b, where a and b are unknown, then log10 y = xlog10 a + blog10 a. Writing m = log10 a and c = blog10 a, the equation becomes y = mx + c which represents a straight line with gradient m and y-intercept c. Hence, plotting log10 y against x should approximately produce a straight line and the values of m, c and hence a, b are relatively easy to estimate. This is a very powerful and clever application of logarithms, that is used widely in experimental science.
EXERCISE 2
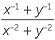 =
= 
EXERCISE 4
- a
- a−pa−q = a
 × a
× a = a
= a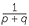 = a−(p + q) = a−p−q
= a−(p + q) = a−p−q - b
- a
 × a
× a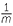 = a
= a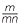 × a
× a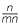 =
=

 m ×
m ×

 n =
n =

 m+n = a
m+n = a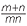 = a
= a +
+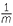
EXERCISE 5
27860000
EXERCISE 6
EXERCISE 7
x = 
EXERCISE 8
a![]() Complete the table of values.
Complete the table of values.
| t | 0 | 1 | 2 | 3 |
| y | 20 | 60 | 180 | 540 |
| b | 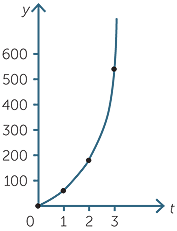 |
||||
c![]() Using a calculator,
Using a calculator,
![]() i
i![]() When t = 0.5, y = 34.64
When t = 0.5, y = 34.64![]() ii
ii![]() When t = 2.5, y = 311.77
When t = 2.5, y = 311.77
![]() iii
iii![]() When t = 2.8, y = 433.48
When t = 2.8, y = 433.48
EXERCISE 9
a![]() log2 32 = x, is equivalent to 2x = 32, so x = 5.
log2 32 = x, is equivalent to 2x = 32, so x = 5.
b![]() log8
log8 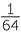 = x, is equivalent to 8x =
= x, is equivalent to 8x = 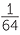 , so x = −2.
, so x = −2.
c![]() log2 x = 5, is equivalent to 25 = x, so x = 32.
log2 x = 5, is equivalent to 25 = x, so x = 32.
d![]() logx 16 = 2, is equivalent to x2 = 16, so x = 4.
logx 16 = 2, is equivalent to x2 = 16, so x = 4.
e![]() log36 x = −
log36 x = − , is equivalent to 36−
, is equivalent to 36− = x, so x =
= x, so x =  .
.
f![]() log7 x = 2, is equivalent to 72 = x, so x = 49.
log7 x = 2, is equivalent to 72 = x, so x = 49.
EXERCISE 10
|
a |
logb x2 + logb x3 − logb x4 |
= 2logb x + 3logb x − 4logb x |
|
|
= logb x |
|
b |
logk |
= logk |
|
|
= logk 1 |
|||
|
= 0 |
|
c |
logb (x2 − a2) − logb (x − a) |
= logb |
|
|
= logb |
|||
|
= logb (x + a) |
EXERCISE 11
log3 x < log2x for x >1 and log2 x < log3 x for x < 1.
EXERCISE 12
1023352 is larger.
EXERCISE 13
7 years
79 months
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()