The Improving Mathematics Education in Schools (TIMES) Project
Fractions and the Index Laws in Algebra
Number and Algebra : Module 32![]() Years : 8-9
Years : 8-9
June 2011
The arithmetic of integers and of fractions.
- Basic methods of mental arithmetic.
- The HCF and LCM in arithmetic.
- Algebraic expressions with whole numbers and negatives.
- The index laws in arithmetic with nonzero whole numbers indices.
- The three index laws involving products in algebra.
- Linear equations
The various uses of algebra require systematic skills in manipulating algebraic expressions. This module is the third of four modules that provide a systematic introduction to basic algebraic skills.
In the module, Algebraic Expressions, we introduced algebra using only whole numbers and the occasional fraction for the pronumerals. Then in the module Negatives and the Index Laws in Algebra we extended the methods of that module to expressions involving negatives.
The present module extends the methods of algebra so that all negative fractions and decimals can also be substituted into algebraic expressions, and can appear as the solutions of algebraic equations.
Although earlier modules occasionally used negative fractions, this module provides the first systematic account of them, and begins by presenting the four operations of arithmetic, and powers, in the context of negative fractions and decimals. The resulting number system is called the rational numbers. This system is sufficient for all the normal calculations of every life, because adding, subtracting, multiplying and dividing rational numbers (apart from division by zero), and taking whole number powers of rational numbers, always produces another rational numbers. In particular, scientific calculations often involve manipulation of equations with decimals.
The module also begins the discussion of algebraic fractions, which routinely cause problems for students. In this module, the discussion is quickly restricted by excluding numerators and denominators with more than one term. These more complicated algebraic fractions are then covered in more detail in the fourth module, Special Expansions and Algebraic Fractions.
Once fractions have been introduced into algebra, the two index laws dealing with quotients can be stated in a more systematic form, and then integrated with algebra. This completes the discussion of the index laws in arithmetic and algebra as far as nonzero whole number indices are concerned.
Our arithmetic began with the whole numbers
![]() 0, 1, 2, 3, 4,…
0, 1, 2, 3, 4,…
We then constructed extensions of the whole numbers in two different directions. First, in the module, Fractions we added the positive fractions, such as 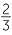 and
and  = 4
= 4 , which can be written as the ratio of a whole number and a non−zero whole number, and we showed how to add, subtract, multiply and divide fractions. This gave a system of numbers consisting of zero and all positive fractions. Within this system, every non−zero number has a reciprocal, and division without remainder is always possible (expect by zero). Only zero has an opposite, however, and a subtraction a − b is only possible when b ≤ a.
, which can be written as the ratio of a whole number and a non−zero whole number, and we showed how to add, subtract, multiply and divide fractions. This gave a system of numbers consisting of zero and all positive fractions. Within this system, every non−zero number has a reciprocal, and division without remainder is always possible (expect by zero). Only zero has an opposite, however, and a subtraction a − b is only possible when b ≤ a.
Secondly, in the module, Integers we started again with the whole numbers and added the opposites of the whole numbers. This gave a system of numbers called the integers, consisting of all whole numbers and their opposites,
![]() …, −3, −2, −1, 0, 1, 2, 3,…
…, −3, −2, −1, 0, 1, 2, 3,…
and we showed how to add, subtract, multiply and divide integers. Within this system of integers, every number has an opposite, and subtraction is always possible. Only 1 and −1 have reciprocals, however, and division without remainder is only possible in situations such as 21 ÷ 7 when the dividend is an integer multiple of the divisor.
Arithmetic needs to be done in a system without such restrictions − we want both subtraction and division to be possible all the time (except for division by zero). To achieve this, we start with the integers and positive fractions that we have already. Then we add the opposites of the positive fractions, so that our number system now contain all numbers such as
![]() −
−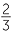
![]() and
and![]() −
− = −4
= −4
All these numbers together are called the rational numbers − the word ‘rational’ is the adjective from ‘ratio’. We have actually been using negative fractions in these notes for some time. These remarks are intended to formalise the situation. The usual laws of signs apply to multiplying and dividing in this larger system, so that a fraction with negative integers in the numerator, or in the denominator, or in both, can be written as either a positive or a negative fraction,
![]()
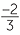
![]() and
and![]()
 = −
= −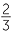
![]() and
and![]()
 =
= 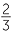
Because of these identities, it is usual to define a rational number as the ratio of an integer and a non−zero integer:
‘A rational number is a number that can be written as a fraction, where a is an integer and b is a non−zero integer’.
Thus positive and negative mixed numerals, terminating decimals, and recurring decimals are rational numbers because they can be written as fractions of integers. For example,
![]() 9
9 =
= 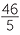 ,
, ![]() −23.917 =
−23.917 = 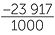 ,
, ![]() −1.
−1.![]()
![]() =
= 
In later modules on topics such as surds, circles, trigonometry and logarithms, we will need to introduce further numbers, called irrational numbers, that cannot be written as fractions. Some examples of such numbers are
![]()
![]() , π, sin 22°, log2 5.
, π, sin 22°, log2 5.
The module, The Real Numbers will discuss the resulting more general system of arithmetic.
EXAMPLE
Show that each number below is rational by writing it as a fraction 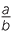 , where a and b are integers with b ≠ 0.
, where a and b are integers with b ≠ 0.
| a | 5 | b |
− |
c |
5 |
|||||
| d | 0.002 | e | −4.7 | f | 1. |
Solution
| a |
5 =  |
b |
− = = 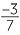 |
c |
5 = = 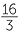 |
|||||
| d |
0.002 =  |
e |
−4.7 = 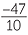 |
f |
1. |
Constructing the rational numbers
There are two ways to construct the rational numbers. The first way is to construct the positive fractions first and then the negatives, which is roughly what happened historically. This involves a three−step procedure:
- 1
- First construct the whole numbers 0, 1, 2, 3, 4,…
- 2
- Then construct the non−negative fractions, such as
 and
and  , as the ratio of two whole numbers, where the second is non−zero. This process involves identifying a fraction such as
, as the ratio of two whole numbers, where the second is non−zero. This process involves identifying a fraction such as 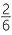 , where the two whole numbers have a common factor, with its simplest form
, where the two whole numbers have a common factor, with its simplest form 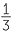 , and identifying a fraction such as
, and identifying a fraction such as  , where the denominator is 1, with the whole number 5.
, where the denominator is 1, with the whole number 5. - 3
- Lastly construct the rational numbers by constructing the opposites of every positive fraction and whole number.
The other method is to construct the integers first and then the fractions. The three steps are now:
- 1
- First construct the whole numbers 0, 1, 2, 3, 4,..
- 2
- Then construct the integers by constructing the opposites …, −4, −3, −2, −1 of all the nonzero whole numbers.
- 3
- Lastly, construct the rational numbers by constructing all the fractions such as
 and
and  the ratio of two integers, where the second is non−zero. This process again involves identifying equivalent fractions, and identifying fractions with denominator 1 as integers.
the ratio of two integers, where the second is non−zero. This process again involves identifying equivalent fractions, and identifying fractions with denominator 1 as integers.
These two procedures are equally acceptable mathematically, and their final results
are identical in structure. Students learn about rational numbers, however, by working
with examples of them in arithmetic and algebra, and there is little to be gained by
such explanations.
Adding and subtracting negative fractions and decimals
When adding and subtracting fractions and decimals that may be positive or negative, the rules are a combination of the rules for integers and the rules for adding and subtracting positive fractions and decimals:
- To subtract a negative number, add its opposite.
- Perform addition and subtraction from left to right.
- When dealing with mixed numerals, it is usually easier to separate the integer part and the fraction.
The following examples demonstrate such calculations first in arithmetical examples, then in substitutions and equations.
EXAMPLE
Simplify:
| a |  + +  - -  − −  - -  |
b | 32.6 + (-23.6) − (-26.4) | ||||
| Solution |
|||||||
| a |  + +  - -  − −  - -  |
=  − − 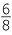 + +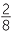 |
b | 32.6 + (−23.6) − (-26.4) | = 32.6 − 23.6 + 26.4 | ||
= 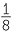 . . |
= 35.4. | ||||||
EXAMPLE
Evaluate −x − y + z when
a![]() x = −20
x = −20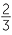 , y = 25
, y = 25 and z = −35
and z = −35 .
. ![]() b
b![]() x = −3.6, y = 5.6 and z = −2.07.
x = −3.6, y = 5.6 and z = −2.07.
Solution
| a |
= − −20 −20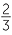  − 25 − 25 + +  −35 −35  |
||
= 20 + 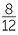 − 25 − − 25 − 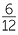 − 35 − − 35 − 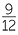 |
|||
= −40 − 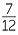 |
|||
= −40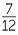 |
- Beware that in notation −40
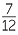 , the negative sign applies to the whole number 40
, the negative sign applies to the whole number 40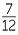 ,
,
so that −40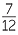 means −
means − 40 +
40 + 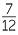
 = −40 −
= −40 −  .
.
| b | −x − y + z | = −(−3.6) −5.6 + (−2.07) | |
| = 3.6 − 5.6 − 2.07 | |||
| = −4.07 |
EXERCISE 1
Simplify −1 +  −
− 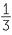 +
+  −
− 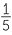 +
+  .
.
Multiplying negative fractions and decimals
As with addition and subtraction, we need to combine the rules already discussed:
- First determine the sign of the product, then deal with the numbers. The product of two positives or two negatives is positive. The product of a positive and a negative is negative.
- In the absence of brackets, the order of operations is:
1 Powers,
2 Multiplication and division from left to right,
3 Addition and subtraction from left to right.
- When multiplying fractions, first convert them to improper fractions.
- When multiplying decimals, convert them to fractions whose denominators are powers of 10.
(Some people prefer to use the rule, ‘Before discarding trailing zeroes, the number of decimal places in the answer equals the total number decimals places in the question.’)
The following examples demonstrate these procedures first in arithmetical examples, then with substitutions and equations.
EXAMPLE
Simplify:
a 2 ×
×  −3
−3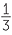
 2 ×
2 ×  −
−
 3
3
![]() b −1.2 × (−0.2)3
b −1.2 × (−0.2)3
Solution
a![]() The product is negative because there are five minus signs in the product.
The product is negative because there are five minus signs in the product.
2 × ×  −3 −3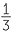  2 × 2 ×  − −  3 3 |
= − × × 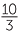 × × 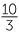 × ×  × ×  × ×  |
|
| = −6 |
b![]() The product is positive because there are four minus signs in the product.
The product is positive because there are four minus signs in the product.
| −1.2 × (−0.2)3 |
= 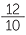 × × 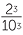 |
|
=  |
||
| = 0.0096 |
EXAMPLE
Simplify −3x2 − yz when:
a![]() x = −1
x = −1 , y = −2
, y = −2 and z = 4
and z = 4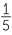
![]() b
b![]() x = 1.1, y = −0.4 and z = −12.1
x = 1.1, y = −0.4 and z = −12.1
Solution
| a | -3x2 − yz |
= -3 ×  × ×  + +  × × 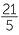 |
|
= -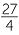 + + 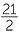 |
|||
= -6 + 10 + 10 |
|||
= -6 − + 10 + + 10 +   means -6 − means -6 −  ). ). |
|||
= 4 −  |
|||
= 3 |
|||
| b | = 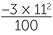 − − 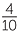 × ×  |
||
= -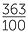 − −  |
|||
| = -1.21 |
EXAMPLE
Solve each equation:
a![]() −
− + 4
+ 4 = −5
= −5
![]() b
b![]()
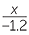 + 2.01 = 2
+ 2.01 = 2
Solution
| a | − + 4 + 4 |
= −5 |
|||
− |
= −10 |
 |
|||
| x | = 31 |
 |
In the last line, it was easier to calculate 3 × 10 = 30 + 1
= 30 + 1 than to use improper fractions
than to use improper fractions
| b | 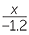 + 2.01 + 2.01 |
= 2 | |||
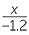 |
= −0.01 |  |
|||
| x | =  × × 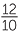 |
 |
|||
| = 0.012 |
EXERCISE 2
How many factors must be taken in the product (−0.8) × 0.9 × (−1.0) × … for the product to exceed 1?
Dividing negative fractions and decimals
We have already reviewed the order of operations. The other necessary rules are:
- First determine the sign of the quotient, then deal with the numbers.
The quotient of two positives or two negatives is positive.
The quotient of a positive and a negative is negative.
- When dividing by a fraction, multiply by its reciprocal. An improper fraction must first be converted to an improper fraction.
- To divide by a decimal, write the calculation as a fraction, then multiply top and bottom by a power of 10 large enough to make the divisor a whole number.
- (Some people prefer to change both decimals to fractions and then use fraction methods.)
EXAMPLE
Simplify:
a![]() 1
1 ÷
÷  −2
−2

![]() b
b![]() 0.9 × (−0.08) ÷ (−0.06)2
0.9 × (−0.08) ÷ (−0.06)2
Solution
| a | 1 ÷ ÷  −2 −2  |
= − × × 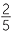 |
||||
= − . . |
||||||
| b | 0.9 × (−0.08) ÷ (−0.06)2 | = 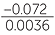 |
||||
= 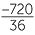 |
(Multiply top and bottom by 10000.) | |||||
| = −20. | ||||||
EXAMPLE
Simplify 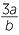 − c when:
− c when:
a![]() a =
a = 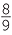 , b = −1
, b = −1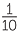 and c = −2.
and c = −2. ![]() b
b![]() a = 0.09, b = −0.027 and c = −0.1.
a = 0.09, b = −0.027 and c = −0.1.
Solution
| a | 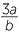 − c − c |
= − × × 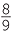 × × 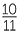 + 2 + 2 |
b | 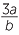 − c − c |
= 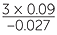 − (−0.1) − (−0.1) |
|||
= −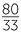 + 2 + 2 |
= −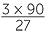 + 0.1 + 0.1 |
|||||||
= −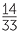 |
= −10 + 0.1 | |||||||
| = −9.9 |
The reciprocal
We have seen that the reciprocal of a positive fraction such as 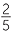 is the fraction
is the fraction  formed by interchanging the numerator and denominator, because
formed by interchanging the numerator and denominator, because
![]()
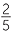 ×
×  = 1
= 1
Similarly, the reciprocal of a negative fraction such as −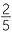 is −
is − , because
, because
![]()
 −
−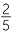
 ×
×  −
−
 = 1
= 1
- To form the reciprocal, interchange numerator and denominator, and do not change the sign.
Reciprocals of positive and negative fractions are important in various later applications, particularly perpendicular gradients.
EXAMPLE
Find, as a mixed numeral when appropriate, the reciprocals of:
a![]() −
−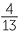
![]() b
b![]()

![]() c
c![]() 5
5
![]() d
d![]() −7
−7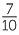
Solution
a![]() The reciprocal of −
The reciprocal of −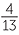 is −
is −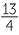 = −3
= −3 .
.
b![]() The reciprocal of
The reciprocal of  is
is  = 5
= 5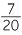 .
.
c![]() The reciprocal of 5
The reciprocal of 5 =
= 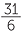 is
is  .
.
d![]() The reciprocal of −7
The reciprocal of −7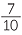 = −
= −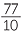 is −
is −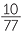 .
.
Compound fractions
There is a very straightforward way to simplify a compound fraction such as 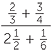
- To simplify a compound fraction, multiply top and bottom by the lowest common denominator of all the fractions.
In the example above, the lowest common denominator of all the fractions is 12, so multiplying top and bottom by 12
![]()
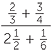 =
= 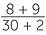 =
= 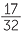
It is also possible to rewrite the fraction as a division 
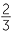 +
+ 
 ÷
÷  2
2 +
+ 
 , but such an approach requires more steps.
, but such an approach requires more steps.
EXAMPLE
a![]() Simplify
Simplify 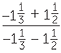
![]() b
b![]() Evaluate
Evaluate 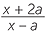 when x = −3
when x = −3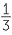 and a =
and a = 
Solution
a![]() Multiply top and bottom by 6.
Multiply top and bottom by 6.
![]()
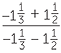 =
= 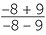 = −
= −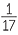
b![]() Multiply top and bottom by 15.
Multiply top and bottom by 15.
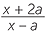 |
= 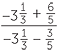 |
|
= 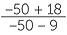 |
||
= 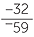 = = 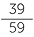 |
Solving equations with fractions
An equation with several fractions can be solved by the standard method, ‘Move every term in x to one side, and all the constants to the other.’ The resulting fraction calculations, however, can be quite elaborate. There is a far quicker approach that gets rid of all the fractions in one single step,
- If an equation involves fractions, multiply by the lowest common denominator.
- Similarly, if an equation involves decimals, multiply through by a suitable power of 10.
The following example uses first this quicker approach, then the standard method, to solve two equations. Compare the approaches and decide for yourself.
EXAMPLE
Use the quicker approach above, and then the standard approach, to solve these equations.
Solve:
a![]() −
− x +
x +  = −3
= −3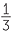
![]() b
b![]() −0.024x + 0.1 = 0.04
−0.024x + 0.1 = 0.04
Solution
a![]() −
− x +
x +  = −3
= −3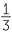
![]() Multiply by 6 to remove all fractions.
Multiply by 6 to remove all fractions.
| −5x + 3 | = −20 |  |
||
| −5x | = −23 |  |
||
| x | = 4 |
 |
||
| or |
− x + x +  |
= −3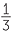 |
|||
− x x |
= −3 − 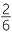 − −  |
 |
||
− x x |
= −3 |
|||
| x | = 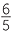 × × 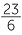 |
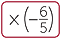 |
||
= 4 |
b![]() −0.024x + 0.1 = 0.04
−0.024x + 0.1 = 0.04
![]() Multiply by 1000 to remove all decimals.
Multiply by 1000 to remove all decimals.
| −24x + 100 | = 40 |  |
||
| −24x | = −60 |  |
||
| x | = 2.5 |  |
||
| or | ||||
| −0.024x + 0.1 | = 0.04 | |||
| −0.024x | = −0.06 |  |
||
= 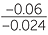 |
 |
|||
= 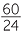 |
||||
| = 2.5 |
EXERCISE 3
Use an efficient method to find the mean of the numbers 1, 0.9, 0.8, …, −2.
The system of rational numbers
We have now introduced four number systems in turn.
First, we introduced the whole numbers 0, 1, 2, 3, 4,… The set of whole numbers is closed under addition and multiplication, which means that when we add or multiply two whole numbers, we obtain another whole number. The whole numbers are not closed under either subtraction or division, however, because, for example,
![]() 7 − 10 is not a whole number
7 − 10 is not a whole number ![]() and
and ![]() 7 ÷ 10 is not a whole number.
7 ÷ 10 is not a whole number.
Next, we added the positive fractions to the whole numbers, so that our number system now contained all non−negative rational numbers, including numbers such as 4, 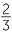 , and 5
, and 5 . This system is closed under division (except by zero), but is still not closed under subtraction.
. This system is closed under division (except by zero), but is still not closed under subtraction.
Then we introduced the integers …, −3, −2, −1, 0, 1, 2, 3, … consisting of all whole numbers and their opposites. This system is closed under subtraction, but not under division.
Now that we are working in the rational numbers − the integers together with all positive and negative fractions − we finally have a system that is closed under all four operations of addition, subtraction, multiplication and division (except by zero). They are also closed under the operation of taking whole number powers.
This set of rational numbers is therefore a very satisfactory system for doing arithmetic, and is quite sufficient for all everyday needs. When we move to the even larger system of real numbers, every real number can be approximated as close as we like by rational numbers (indeed by terminating decimals), so that the rational numbers will remain extremely important.
Cancelling, multiplying and dividing algebraic fractions
An algebraic fraction is a fraction involving pronumerals,
![]()
 ,
,  ,
, 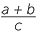 , −
, −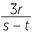 .
.
The pronumerals in the fraction represent numbers, so we deal with algebraic fractions using exactly the same procedures that we use in arithmetic.
Substitution into algebraic fractions
We have seen in arithmetic that the denominator in a fraction cannot be zero. This means that:
In the expression  , we cannot substitute x = 0.
, we cannot substitute x = 0.
In the expression 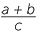 , we cannot substitute c = 0.
, we cannot substitute c = 0.
In the expression −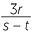 , we cannot substitute the same value for s and t.
, we cannot substitute the same value for s and t.
Apart from this qualification, substitution into algebraic fractions works exactly the same as substitution into any algebraic expression. For example, if r = 5, s = 7 and t = 4, then
![]() −
−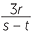 =
= 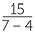 = 5
= 5
Substitution of negative numbers requires the usual care with signs. If r = −2, s = −7 and
t = 5,
![]() −
−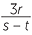 =
= 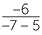 =
= 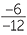 =
= 
EXAMPLE
a![]() What value of a cannot be substituted into
What value of a cannot be substituted into 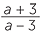 ?
?
b![]() What value of a makes
What value of a makes 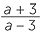 zero?
zero?
c![]() Evaluate
Evaluate 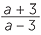 when a = −2 .
when a = −2 .
Solution
- a
- When a = 3, the denominator is zero, and the expression cannot be evaluated.
- b
- When a = −3, the numerator is zero but the denominator is not zero, so the expression is zero.
| c | When a = −2, | 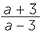 |
= 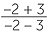 |
||
= 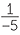 |
|||||
= − |
The rest of this module will exclude denominators, such as s − t and a − 3, that have two or more terms. Such expressions will be considered in the later module, Special Expansions and Algebraic Fractions.
Cancelling algebraic fractions
Because pronumerals are just numbers, we can cancel both pronumerals and numbers in an algebraic fraction. For example,
![]()
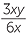 =
= 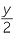
![]() and
and ![]()
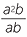 = a.
= a.
We cannot cancel zero, so strictly we should exclude zero values of the pronumeral when we cancel. This would mean writing
![]()
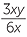 =
= 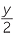 provided x ≠ 0
provided x ≠ 0 ![]() and
and![]()
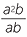 = a provided a ≠ 0 and b ≠ 0.
= a provided a ≠ 0 and b ≠ 0.
Such qualifications become important much later in calculus. At this stage, however, it is not appropriate to bring the matter up, unless students insist.
EXAMPLE
Simplify each algebraic fraction by cancelling any common factors:
| a | 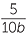 |
b | 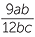 |
c | 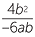 |
d | 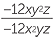 |
|||||||
|
Solution |
||||||||||||||
| a | 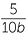 = =  |
b | 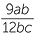 = =  |
c | 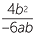 = − = −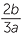 |
d | 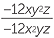 = = 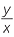 |
|||||||
Dividing algebraic expressions
When we divide, the laws of signs are the same as the laws for multiplying:
- The quotient of two negatives or two positives is positive.
- The quotient of a positive and a negative is negative.
The following examples illustrate all the possibilities:
![]()
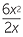 = 3x
= 3x ![]()
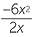 = −3x
= −3x ![]()
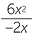 = −3x
= −3x ![]()
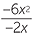 = 3x
= 3x
As with multiplication, there are three steps in handling more complicated expressions:
- First deal with the signs.
- Then deal with the numerals.
- Then deal with each pronumeral in turn.
![]()
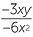 =
= 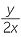
![]() and
and ![]() (21abc2) ÷ (−7b2c) = −
(21abc2) ÷ (−7b2c) = −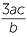
The last answer can also be written as 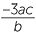 or even as
or even as  , but the best way to write the answer −
, but the best way to write the answer −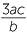 , with the negative sign out the front of the fraction.
, with the negative sign out the front of the fraction.
Fraction notation is usually used for quotients, but the division sign can also be used, as in the second example above.
EXAMPLE
Simplify each quotient:
| a | b | 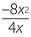 |
c | 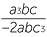 |
d | 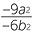 |
||||||||
|
Solution |
||||||||||||||
| a | (−12ab) ÷ (−3bc) = 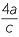 |
b | 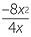 = −2x = −2x |
|||||||||||
| c | 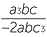 = − = −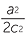 |
d | 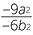 = =  |
|||||||||||
Multiplying algebraic fractions
We have seen how to multiply fractions in arithmetic,
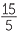 × ×  − −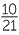  |
=− × × 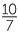 |
|
= −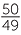 |
- First deal with the signs.
- Then cancel any common factors from a numerator and a denominator.
- Then multiply the numerators, and multiply the denominators.
![]() Exactly the same method applies to multiplying algebraic fractions. For example,
Exactly the same method applies to multiplying algebraic fractions. For example,
 × ×  − −  |
=- × ×  |
 − −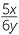  × ×  − −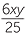  |
=  × ×  |
||
= − |
= 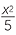 |
EXAMPLE
Simplify:
| a |  − −  × ×  − −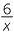  |
b | 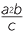 × ×  − −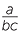  |
|||||
|
Solution |
||||||||
| a |  − −  × ×  − −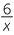  |
=  × ×  |
b | 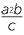 × ×  − −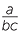  |
= −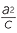 × ×  |
|||
| = 4 | = − |
|||||||
Dividing by an algebraic fraction
We know the law of signs for division, and we know how to divide by a fraction. To divide by an algebraic fraction, we apply these same laws in succession
- First determine the sign of the quotient.
- To divide by a fraction, multiply by its reciprocal
For example,
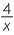 ÷ ÷  − −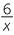  |
= −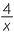 × ×  |
 ÷ ÷  |
=  × ×  |
|
= − × ×  |
=  × ×  |
|||
= − |
= 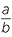 |
EXAMPLE
Simplify each quotient:
| a | 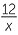 ÷ ÷  |
b | 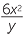 ÷ ÷ 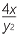 |
c | 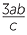 ÷ (−6abc) ÷ (−6abc) |
d |  − −  ÷ ÷  − −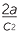  |
Solution
| a | 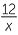 ÷ ÷  |
= 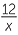 × ×  |
b | 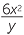 ÷ ÷ 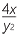 |
= 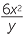 × × 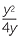 |
|||
=  × ×  |
= 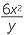 × × 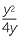 |
|||||||
| = 4 | = 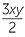 |
| c | 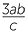 ÷ (−6abc) ÷ (−6abc) |
= 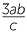 × ×  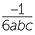 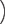 |
d |  − − 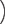 ÷ ÷  − −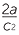 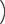 |
=  × × 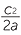 |
|||
= −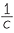 × × 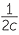 |
=  × ×  |
|||||||
= −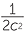 |
= ac |
The reciprocal of an algebraic fraction
Reciprocals of algebraic fractions are formed in exactly the same way as was done
in arithmetic.
The reciprocal of 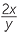 is
is 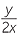 , because
, because 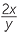 ×
× 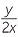 = 1.
= 1.
The reciprocal of −a3 is − , because (−a3) ×
, because (−a3) ×  −
−
 = 1.
= 1.
The reciprocal of −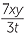 is −
is −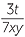 , because
, because  −
−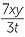
 ×
×  −
−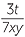
 = 1.
= 1.
- To form the reciprocal, interchange numerator and denominator, and do not change the sign.
EXAMPLE
Write down the reciprocal of each algebraic fraction:
| a | 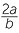 |
b | −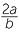 |
c | 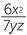 |
d | −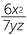 |
|||||||
|
Solution |
||||||||||||||
| a | 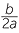 |
b | −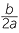 |
c | 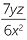 |
d | −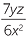 |
|||||||
The previous algebra module Negatives and the Index Laws in Algebra dealt with the index laws for a product of powers of the same base, for a power of a power, and for
a power of a product:
- To multiply powers of the same base, add the indices:
- am × an = am+n.
- To raise a power to a power, add the indices:
- (am)n = amn.
- The power of a product os the product of the powers:
- (ab)n = anbn.
In these identities, a and b are any numbers, and m and n are any nonzero
whole numbers.
We now turn to the remaining two index laws, which involve quotients.
The index law for the power of a quotient
To see what happens when we take a power of a fraction, we simply write out the power.
   3 3 |
=  × ×  × ×  |
 |
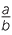  5 5 |
= 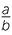 × × 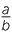 × × 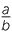 × × 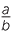 × × 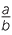 |
=  |
= 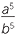 |
The general situation can thus be expressed as:
- The power of a quotient is the quotient of the powers:
![]()

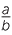
 n =
n = 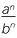 where a and b ≠ 0 are numbers, and n is a nonzero whole number.
where a and b ≠ 0 are numbers, and n is a nonzero whole number.
The following examples illustrate the use of the law in arithmetic and algebra.
EXAMPLE
Simplify:
| a |  − −  5 5 |
b |  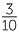  4 4 |
c |  −4 −4  2 2 |
d |  3 3  3 3 |
Solution
| a |  − −  5 5 |
= −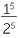 |
b |  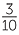  4 4 |
= 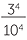 |
|||
= −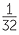 |
= 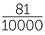 |
| c |  −4 −4  2 2 |
=  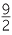  2 2 |
d |  3 3  3 3 |
=  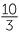  3 3 |
|||
= 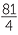 |
= 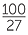 |
|||||||
= 20 |
= 37 |
When applied to an algebraic fraction, the laws previously introduced for the power of a product and for the power of a power, are often required as well. For example,
![]()

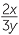
 3 =
3 = 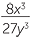
![]() and
and![]()


 2 =
2 = 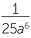
EXAMPLE
Expand the brackets:
a![]()

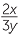
 2
2 ![]() b
b![]()
 −
−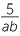
 3
3 ![]() c
c ![]()

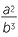
 2
2![]() d
d![]()

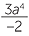
 4
4
Solution
| a |  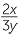  2 2 |
= 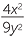 |
b |  − −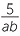  3 3 |
= −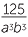 |
||||
| c |  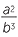  2 2 |
= 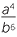 |
d |  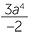  4 4 |
= 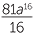 |
The index law for the quotient of powers of the same base
The remaining index law from arithmetic deals with dividing powers of the same base. The module Multiples, Factors and Powers developed the law in the form, ‘To divide powers of the same base, subtract the indices’. For example,
![]() 75 ÷ 73 = (7 × 7 × 7 × 7 × 7) ÷ (7 × 7 × 7) = 72.
75 ÷ 73 = (7 × 7 × 7 × 7 × 7) ÷ (7 × 7 × 7) = 72.
Fractions, however, had not been introduced at that stage, so the divisor could not be a higher power than the dividend. Now that we have fractions, we can express the law in fractional notation and do away with the restriction:
 |
= 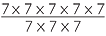 |
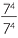 |
= 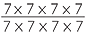 |
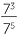 |
= 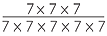 |
||
| = 72 | = 1 | =  |
The base can also be a pronumeral, and the law can now be written as:
- To divide powers of the same base, subtract the indices.
For example,
![]()
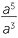 = a2 and
= a2 and 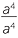 = 1 and
= 1 and 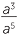 =
=  .
.
Later, when zero and negative indices have been introduced in the module The Index Laws, we will be able to state this law in its usual, more concise form:
![]()
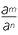 = am−n.
= am−n.
EXAMPLE
Simplify each expression:
| a | 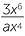 |
b | 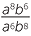 |
c |  × ×  |
d | a3b2 ÷ a6b6c6 | |||||||
|
Solution |
||||||||||||||
| a | 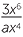 = =  |
b | 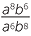 = = 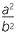 |
c |  × ×  = = 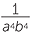 |
d | a3b2 ÷ a6b6c6 = 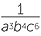 |
|||||||
Adding and subtracting algebraic fractions
When a set of algebraic fractions have a common denominator, it is straightforward to add them. As always, we collect like terms,
![]()
 +
+ 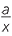 −
−  +
+ 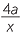 =
= 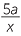 −
−  (which is perhaps written as
(which is perhaps written as 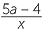 )
)
EXAMPLE
Simplify each expression:
| a |  − − 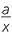 − −  |
b | 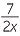 − − 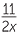 − − 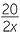 |
|||
|
Solution |
||||||
| a |  − − 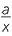 − −  = =  − − 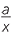 , or − , or −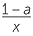 |
b | 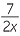 − − 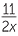 − − 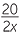 = − = −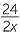 = − = −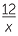 |
|||
Using a common denominator
When the fractions do not have a common denominator, we need to find the lowest common denominator, just as we did for arithmetic fractions. We shall restrict the discussion to numerical denominators at this stage, and leave denominators with pronumerals to the module Special Expansions and Algebraic Fractions.
 − −  |
= 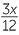 − − 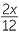 |
|
= 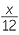 . . |
EXAMPLE
Simplify each expression:
| a |  − −  + +  + + 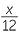 |
b | 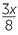 _ _  |
|||||
|
Solution |
||||||||
| a |  − −  + +  + + 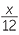 |
= 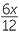 _ _ 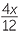 + + 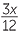 + + 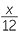 |
b | 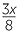 _ _  |
= 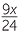 _ _  |
|||
= 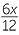 |
= −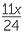 |
|||||||
=  |
||||||||
As mentioned in the Motivation section, this module is the third of four modules dealing with basic manipulation of algebraic expressions. The four modules are:
- Algebraic Expressions
- Negatives and the Index Laws in Algebra
- Fractions and the Index Laws in Algebra (the present module)
- Special Expansions and Algebraic Fractions
Algebraic fractions have been introduced in this module, but the algebra of algebraic fractions can cause considerable difficulty if it is introduced in full strength before more fundamental skills have been assimilated. Algebraic fractions will therefore be considered in more details in the fourth module Special Expansions and Algebraic Fractions.
The index laws will be greatly expanded in scope once negative and fractional indices are introduced in the module Indices. One piece of clumsiness in the present module concerned the quotient of the difference of powers, where we needed to write down three different examples
![]()
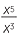 = x2
= x2 ![]() and
and![]()
 = 1
= 1 ![]() and
and![]()
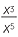 =
= 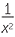 .
.
Once the zero index and negative indices are brought into algebra, all this can be replaced with the single law
![]()
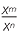 = xm − n where m and n are integers.
= xm − n where m and n are integers.
Square roots and cube roots can also be represented using fractional indices − for example, ![]() is written as 5
is written as 5 and
and ![]() is written as 5
is written as 5 − and yet the five index laws still hold even when the index is any rational number. Negative and fractional indices are introduced in the module, Indices and Logarithms. Later in calculus, an index can be any real number.
− and yet the five index laws still hold even when the index is any rational number. Negative and fractional indices are introduced in the module, Indices and Logarithms. Later in calculus, an index can be any real number.
EXERCISE 1
The lowest common denominator is 60. Grouping the numbers in pairs before adding them all reduces the size of the numerator.
| Sum | =  -1 + -1 +   + +  - - + +   + +  - - + +   |
|
= - − − 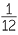 − −  |
||
= -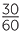 − −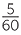 − −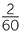 |
||
= -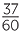 |
EXERCISE 2
We can ignore all negative products. Since (−0.8) × 0.9 × (−1.0) × 1.1 is less than 1, the first
product greater than 1 is (−0.8) × 0.9 × (−1.0) × 1.1 × (−1.2) × 1.3 × (−1.4).
EXERCISE 3
One approach is to notice that when the 31 numbers are added, the first 21 numbers cancel out. The remaining 10 numbers can then be added by grouping them in pairs:
| 1 + 0.9 + 0.8 +…+ (-2) | = -1.1 − 1.2 − 1.3 − … −2. |
| = (-1.1 − 2)+(-1.2 − 1.9)+(-1.3 − 1.8)+(-1.4 − 1.7)+(-1.5 − 1.6) | |
| = −3.1 × 5 | |
| = −15.5. |
Hence mean = 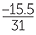 =
= 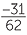 = −0.5.
= −0.5.
A better approach is realise that −0.5 is the middle number, and that the other 30 numbers fall into pairs equally spaced one to the left and one to the right of −0.5. Hence the mean is −0.5.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


