Year 8

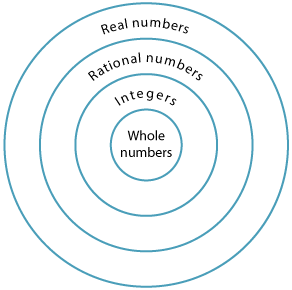
From the beginning of their mathematical studies, students are introduced to the whole numbers, that is, 0, 1, 2, …. Later, fractions and decimals are introduced, leading to the notion of a rational number, then the integers and negative fractions are covered. Next, Pythagoras' theorem and circumference of a circle help to introduce the notion of irrational numbers.

Detailed description

The term rational numbers is used for positive and negative fractions including the integers. The rational numbers are numbers of the form \(\dfrac{a}{b}\) where a is an integer and b a non-zero integer. An irrational number is a number which is not rational.

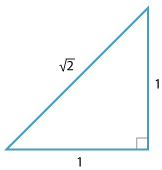
The integers and rational numbers arise naturally from the ideas of arithmetic. The real numbers essentially arise from geometry. Finding the length of the diagonal of a square leads to square roots of numbers that are not squares.

When we draw a circle whose radius is a whole number and ask for its circumference and area, the answer involves the irrational number π.

It was as a consequence of Pythagoras' theorem that the Greeks discovered irrational numbers, which shook their understanding of number to its foundations. They also realised that several of their geometric proofs were no longer valid. The Greek mathematician Eudoxus considered this problem and mathematicians remained unsettled by irrational numbers for a very long time. The modern understanding of real numbers only began to be developed during the 19th century.