Year 9
Measurement and Geometry
Surface area and volume of prisms and cylinders
A polyhedron is a solid bounded by polygons. A right prism is a polyhedron that has two congruent and parallel faces (called the base and top), and all its remaining faces are rectangles. This means that when a right prism is stood on its base, all the walls are vertical rectangles. We will generally say 'prism' when we really mean 'right prism'. A prism has uniform cross-section. This means that when you take slices through the solid parallel to the base, you get polygons congruent to the base. So the area of each slice is always the same. In a rectangular prism, the cross-section is always a rectangle.
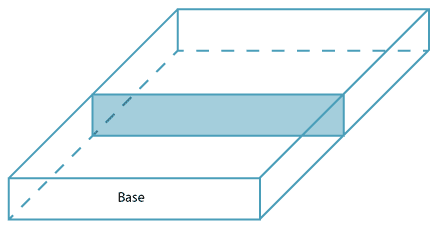
The word 'prism' comes from the Greek word that means 'to saw'. If we cut or saw through a prism parallel to its base, the cross-sectional area is always the same.
Naming prisms and cylinders
A prism is named by the shape of its base.
A rectangular prism has a rectangular base and hence a rectangular cross-section.

A triangular prism has a triangular base and hence a triangular cross-section.

A cylinder has a circular base and hence a circular cross-section.

We encounter prisms and cylinders everywhere; most boxes are rectangular prisms, most rooms are rectangular prisms, most cans are cylinders. When we find out how much cardboard there is in the box, when we need the area of the walls to paint in a room, or when we need to find how much tin is needed to make a can, we are finding the surface area of prisms and cylinders. When we find out how much milk is in the container, how much soup is in the can, and how much chocolate is in the packet, we are finding the volume of prisms and cylinders.